Les matemátiques discretes son una área de les matemátiques encargaes del estudiu de los conxuntos discretos: finitos o infinitos numerables.
N'oposición a les matemátiques continues, que s'encarguen del estudiu de conceutos como la continuidá y el cambéu continuu, les matemátiques discretes estudien estructures que los sos elementos pueden cuntase ún por ún xebradamente. Esto ye, los procesos en matemátiques discretes son contables, como por casu, los númberos enteros, grafos y sentencies de lóxica.[1]
Ente que el cálculu infinitesimal ta fundáu nos númberos reales que nun son numerables, la matemática discreta ye la base de too rellacionar colos númberos naturales o conxuntos numerables.
Son fundamentales pa la ciencia de la computación, porque solo son computables les funciones de conxuntos numerables.[ensin referencies]
La clave en matemátiques discretes ye que nun ye posible remanar les idees de proximidá o llende y suavidá nes curves, como se puede nel cálculu. Por casu, en matemátiques discretes una incógnita puede ser 2 o 3, pero nunca se va averar a 3 pela izquierda con 2.9, 2.99, 2.999, etc. Les gráfiques en matemátiques discretes vienen daes por un conxuntu finito de puntos que pueden cuntase por separáu; esto ye, los sos variables son discretes o dixitales, ente que les gráfiques en cálculu son trazos continuos de rectes o curves; esto ye, los sos variables son continues o analóxiques.
Historia
Les matemátiques discretes vieron un gran númberu de problemes difíciles de resolver. En teoría de grafos, muncha de la investigación realizada nos sos entamos foi motivada por intentos pa probar el teorema de los cuatro colores, que foi probáu más de cien años dempués de la so inicial descripción. El problema de les pontes de Königsberg, un problema clásicu del prolíficu Leonhard Euler.
En lóxica, el segundu problema de la llista de problemes abiertos de David Hilbert, yera probar que los axomes de l'aritmética son consistentes. El segundu teorema de Gödel de la incompletitud probó en 1931 qu'esto nun ye posible, a lo menos dientro de l'aritmética en sí. El décimu problema de Hilbert yera determinar si un polinomiu diofántico con coeficientes enteros dadu tien una solución entera. En 1970, Yuri Matiyasevich probó qu'esto ye imposible de faer.
La necesidá de descifrar códigos alemanes na Segunda Guerra Mundial dio pasu a meyores na criptografía y la ciencia computacional teórica, col primer ordenador electrónicu, dixital y programable desenvueltu n'Inglaterra. Coles mesmes, requerimientos militares motivaron meyores na investigación d'operaciones. La Guerra Fría tuvo significancia na criptografía, y caltener vixente, colo que se realizaron meyores na criptografía asimétrica.
Anguaño, unu de los problemes abiertos más famosos na teoría de la informática ye'l problema de les clases de complexidá "P = NP". El Clay Mathematics Institute ufiertó un premiu d'un millón de dólares pa la primer demostración correuta, xunto con premios pa 6 problemes más.
Tópicos na matemática discreta
Informática teórica

La teoría de la informática inclúi árees de la matemática discreta relevante a la computación. Ta altamente rellacionada con teoría de grafos y lóxica. Dientro de la teoría de la informática atópase la teoría d'algoritmos pa problemes matemáticos. La computabilidad estudia lo que puede ser computáu y tien llazos fuertes cola lóxica, ente que la complexidá estudia'l tiempu que se precisa pa faer los cálculos. La teoría d'autómates, los llinguaxes formales y la Dinámica de sistemes rellacionar de manera cercana cola computabilidad. Les redes de Petri y álxebra de procesos usar pa modelar sistemes de cálculu, y los métodos de la matemática discreta usar p'analizar circuitos VLSI. La xeometría computacional aplica algoritmos a problemes xeométricos, ente que l'analís dixital d'imáxenes aplicar a representaciones d'imáxenes. La teoría informática tamién inclúi l'estudiu de tópicos d'informática continua.
Teoría de la información

La teoría de la información vese arreyada na cuantificación de la información. Cercanamente rellacionáu a esto ye la teoría de codificación, que ye usada pa diseñar métodos de tresmisión y almacenamientu de datos eficientes y confiables. La teoría de la información tamién inclúi tópicos continuos tales como señales análogicas, codificación análoga y cifráu análogu.
Lóxica
La lóxica ye l'estudiu de los principios del razonamientu válidu y la inferencia, como tamién de la consistencia, solidez y completitud. Por casu, na mayoría de los sistemes na lóxica, la llei de Peirce, (((P→Q)→P)→P) ye un teorema. En lóxica clásica, pue ser fácilmente verificáu con una tabla de verdá. L'estudiu de les demostraciones matemátiques ye particularmente importante en lóxica y tien aplicaciones na demostración automática de teoremas y verificación formal de software.
Les fórmules lóxiques son estructures discretes, como lo son les demostraciones, que formen árboles finitos, o más xeneralmente, estructures de grafos acíclicos (en cada pasu d'inferencia combinando una o más cañes de premises pa dar una sola conclusión). Les tables de verdá de fórmules lóxiques usualmente formen un conxuntu finito, xeneralmente acutáu a dos valores: verdaderu y falsu, pero la lóxica puede tener valores continuos, por casu na lóxica difusa. Los conceutos como árboles de demostraciones o derivaciones infinites tamién fueron estudiaos, por casu na lóxica proposicional infinitaria.
Teoría de conxuntos
La teoría de conxuntos ye la caña de la matemática qu'estudia conxuntos matemáticos, que son coleiciones d'oxetos, tales como {azul, blancu, colloráu} o'l conxuntu infinitu de tolos númberos primos. Conxuntos parcialmente ordenaos y conxuntos con otres rellaciones tienen aplicación en munches árees.
Na matemática discreta, los conxuntos numerables (incluyendo conxuntos finitos) son el principal oxetu d'estudiu. L'entamu de la teoría de conxuntos xeneralmente rellaciónase col trabayu de Georg Cantor, faciendo distinción ente distintos tipos de conxuntos infinitos, motiváu pol estudiu de les series trigonométriques. El desenvolvimientu más fondu na teoría de conxuntos infinitos ta fora del algame de la matemática discreta. Ello ye que el trabayu contemporaneu en teoría descriptiva de conxuntos fai usu estensu del usu de la matemática continua tradicional.
Combinatoria
La combinatoria ye la caña de la matemática qu'estudia coleiciones finitas d'oxetos que pueden ser combinaos o ordenaos.
La combinatoria enumerativa ocúpasesobremanera, del "recuentu" de los oxetos de diches coleiciones.
La combinatoria analítica concentrar na enumeración d'estructures combinatories utilizando ferramientes d'analís complexu y teoría de probabilidá. En contraste cola combinatoria enumerativa, qu'usa fórmules combinatories esplícites y funciones xeneradores pa describir los resultaos, la combinatoria analítica enfocar en llograr fórmules asintóticas.
La teoría de diseñu ye l'estudiu de diseños combinatorios, que son clases de subconxuntos con ciertes propiedaes numbériques d'intersección.
La teoría de particiones estudia dellos problemes asintóticos y de enumeración rellacionaos con particiones enteres, y ta rellacionada con series q, funciones especiales y polinomios ortogonales. Orixinalmente una parte de teoría numbérica y analís, la teoría de particiones ye considerada una parte de combinatoria, o una área independiente.
La teoría del orde ye l'estudiu de conxuntos parcialmente ordenaos, finitos ya infinitos.
Teoría de grafos
La teoría de grafos ye l'estudiu de grafos y la teoría de redes. Xeneralmente ye considerada parte de la Combinatoria, pero evolucionó pela so parte lo suficiente como pa ser considerada una materia por si mesma.[2] La teoría de grafos tien estenses aplicaciones en toles árees de la matemática y la ciencia. Esisten, inclusive, grafos continuos.
Teoría de distribuciones de probabilidá discretes
La teoría de distribuciones discretes trata con eventos qu'asoceden n'espacios de muestra numerables. Por casu, conteos como'l númberu d'aves nuna bandada solo pueden tener valores naturales {0, 1, 2,...}. Per otra parte, observaciones continues como los pesos d'estes aves pueden representase por aciu númberos reales, y típicamente seríen modelaos por una distribución de probabilidá continua, como por casu, la distribución normal. Distribuciones continues pueden ser utilizaes p'averar discretes y viceversa. Pa situaciones nes cualos los valores posibles son altamente acutaos na so variabilidá, como por casu en dados o cartes, calcular les probabilidaes a cencielles precisa de combinatoria enumerativa.
Teoría de númberos

La teoría de númberos principalmente tien que ver coles propiedaes de los númberos polo xeneral y, particularmente, de los enteros. Tien aplicaciones na criptografía, criptoanálisis y criptología, particularmente no que refier a númberos primos. Otros aspeutos de la teoría de númberos inclúi la teoría xeométrica de númberos. Na teoría analítica de númberos, tamién s'utilicen téuniques de matemática continua.
Álxebra
Les estructures alxebraiques asoceden discreta y de cutio. Como exemplos d'álxebres discretes tán: el álxebra booleana, utilizada en circuitos dixitales y programación, álxebra relacional, utilizada en bases de datos; grupos, finitos y discretos, según aniellos y campos son importantes na teoría de códigos.
Cálculu de diferencies finitas
Una función definida nun intervalu d'enteros llámase secuencia. Una secuencia puede ser una finita o infinita. Tal función discreta pue ser definida explícitamente por una llista (si'l so dominiu ye finito), o por una fórmula pal so términu n-esimo, o tamién puede ser dada implícitamente por una rellación de recurrencia o ecuación de diferencia. Les ecuaciones de diferencia son similares a les ecuaciones diferenciales pero reemplácense les derivaes tomando la diferencia ente términos axacentes y pueden ser utilizaes p'averar ecuaciones diferenciales. Munches interrogantes y métodos de les ecuaciones diferenciales tienen les sos contrapartes pa ecuaciones de diferencies.
Xeometría

La xeometría discreta y la xeometría combinatoria traten les propiedaes combinatories de coleiciones discretes d'oxetos xeométricos. Un antiguu tópicu na xeometría discreta ye'l recubrimientu del planu. La xeometría computacional aplica algoritmos a problemes xeométricos.
Topoloxía
Magar la topoloxía xeneral ye'l campu de les matemátiques que formaliza y xeneraliza la noción intuitiva de "deformación continua" de los oxetos, o'l procesu de llende, da pasu a munchos tópicos discretos. Esto pue ser atribuyíu en parte a l'atención que se-y da a los invariantes topolóxicos, que tomen, polo xeneral, valores discretos. Ente les sos cañes d'estudiu atopen la topoloxía combinatoria, topoloxía de grafos, topoloxía computacional y topoloxía alxebraica, ente otros.
Investigación d'operaciones

La investigación d'operaciones ye una caña de les matemátiques consistente nel usu de modelos matemáticos, estadística y algoritmos con oxetu de realizar un procesu de toma de decisiones práutiques pa negocios y otres árees. Estos problemes pueden ser, por casu, la repartición de recursos pa maximizar ingresos, o agendar actividaes pa embrivir riesgos. Téuniques propies de la investigación d'operaciones inclúin programación llinial y otres árees d'optimización, teoría de coles, algoritmo de planificación, analís de redes. La investigación d'operaciones tamién inclúi tópicos continuos como procesos de Markov de tiempu continuu, optimización de procesos, martingales de tiempu continuu, etc.
Teoría de xuegos, teoría de la decisión, teoría d'utilidá
La teoría de la decisión trata fundamentalmente con identificar los valores, incertidumes y otros factores relevantes nuna decisión, la so racionalidá y la decisión óptima resultante.
La teoría d'utilidaes ye sobre midíes del relativu prestu económicu proveniente del consumu de dalgún bien o serviciu.
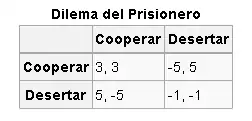
La teoría de xuegos trata coles situaciones onde l'ésitu depende de les decisiones d'otros, lo cual fai escoyer el meyor cursu d'aición más complexu. Tópicos inclúin la Teoría de puya y la división xusta.
La teoría de decisión social estudia les elecciones.
Discretización
La discretización busca tresformar modelos y ecuaciones continuos nes sos contrapartes discretes,[3] usualmente pa faer cálculos más fácilmente utilizando aproximamientos. L'analís numbéricu ye un importante exemplu.
Ver tamién
- álxebra llinial – l'estudiu de funciones lliniales rellacionaes.
- algoritmia – l'estudiu de métodos de cálculos.
- combinatoria
- investigación d'operaciones
- lóxica – l'estudiu del razonamientu *
probabilidá y cadenes de Markov
- teoríes de la computabilidad y de la complexidá - que traten sobre la viabilidá y llendes de los algoritmos
- teoría de conxuntos – estudiu de coleiciones d'oxetos
- teoría de grafos
- teoría de la información
- teoría de númberos
- topoloxía alxebraica
Referencies
- ↑ Weisstein, Eric W. «Matemátiques discretes» (inglés). MathWorld. Wolfram Research.
- ↑ Graphs on Surfaces, Bojan Mohar and Carsten Thomassen, Johns Hopkins University press, 2001
- ↑ http://ccc.inaoep.mx/~emorales/Cursos/KDD/node155.html Discretización de Valores
Enllaces esternos
- matemátiques discretes (n'inglés)