Lleis de Kepler
llei física

Esquema de la Primera Llei de Kepler.

Esquema de la Segunda Llei de Kepler.

Esquema de la Tercera Llei de Kepler, o llei harmónica. Val pa los planetes Uranu, Neptunu y Plutón, afayaos tiempu dempués de la muerte de Kepler.

Les lleis de Kepler foron enunciaes por Johannes Kepler pa esplicar el movimientu de los planetes nes sos órbites alredor del Sol. Anque él nun les enunció nel mesmu orde, anguaño les lleis numbérense comu vien:

• Primera Llei (1609): Tolos planetes desplacense alrodiu'l Sol describiendo órbites elíptiques, tando'l Sol asitiáu nún de los focos.

• Segunda Llei (1609): El radiovector que xune'l planeta y el Sol barre árees iguales en tiempos iguales.

El vector posición de cualesquier planeta respeutu'l Sol, barre árees iguales de la elipse en tiempos iguales.

La llei de les árees ye equivalente a la constancia del momentu angular, ye dicir, cuando'l planeta ta más alloñáu del Sol (afeliu) la so velocidá ye menor que cuando ta más cercanu al Sol (periheliu). Nel afeliu y nel periheliu, el momentu angular L ye'l productu de la masa del planeta, pola so velocidá y pola so distancia al centru'l Sol.

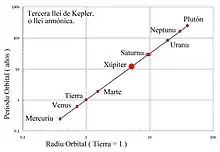
• Tercera Llei (1618): Pa cualquier planeta, el cuadráu del so periodu orbital (tiempu que tarda en dar una vuelta alredor del Sol) ye direutamente proporcional al cubu de la distancia media col Sol.

onde P ye'l periodu de rotación alredor del Sol medíu n'años, y a la distancia del planeta al Sol, midida n'Unidaes Astronómiques (U.A.). Una unidá astronómica ye la distancia Tierra - Sol. Xúpiter, por exemplu, ta a 5 unidaes astronómiques del Sol, y ${\displaystyle a^{3}}$ = 5 x 5 x 5 = 125. El númberu que multiplicáu por sigo mesmu da 125 ye'l 11. Y 11 años ye'l periodu de tiempu que Xúpiter necesita pa dar un vuelta alredor del Sol

Estes lleis aplíquense a otros cuerpos astronómicos que s'alcuentren en mutua influyencia gravitatoria como'l sistema formáu pola Tierra y la Lluna.

Formulación de Newton de la 3ª llei de Kepler

Kepler deduxo les sos lleis a partir d'observaciones astronómiques precises obteníes por Tycho Brahe y, anque sabía qu'esplicaben el movimientu planetariu observáu, nun entendía les razones d'esti comportamientu. La presentación de Kepler incorporaba una bayura detalles ya inclusive especulaciones metafísiques. Foi Isaac Newton el que sacó de los escritos de Kepler la formulación matemática precisa de les lleis. Newton foi quien a rellacionar estes lleis colos sos propios descubrimientos, dando un sentíu físicu precisu a lleis empíriques. L'estudiu de Newton de les lleis de Kepler conduxo a la so formulación de la llei de la gravitación universal.

La formulación matemática de Newton de la tercera llei de Kepler ye:

${\displaystyle P^{2}={\frac {4\pi ^{2}}{G(m_{1}+m_{2})}}a^{3}}$

Onde, P ye'l periodu orbital, a ye'l semiexe mayor de la órbita, m₁ y m₂ les mases del cuerpu central y el cuerpu orbitante respeutivamente y G una constante denomada Constante de gravitación universal de la que'l valor marca la intensidá de la interacción gravitatoria y el sistema d'unidaes a utilizar pa les otres variables d'esta espresión.

Universalidá de les lleis de Kepler

Les lleis de Kepler nun son solamente aplicables a los planetes sinón que tamién a una masa que se desplaza pel espaciu n'órbita alredor d'otra masa. Ye'l casu, por exemplu, de la Lluna y la Tierra o d'un satélite artificial n'órbita alredor d'ella.

Esta llei nun ye aplicable más qu'a mases suficientemente grandes. Asina, pal desplazamientu d'un electrón alredor del nucleu d'un átomu, entramos nel dominiu de la física cuántica, que nun obedez a les mesmes lleis (estos cuerpos tán muncho más influenciaos pola atraición electrostática que poles fuercies gravitatories).