Interseición de conxuntos
operación de conxuntos, operación binaria, interseición y interseición de dellos conxuntos
soconxuntu

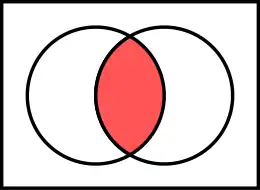La interseición ye una operación ente conxuntos. Esta operación cria un conxuntu, denomáu conxuntu interseición, al que pertenecen tolos elementos que pertenecen al empar a tolos conxuntos que s'intersequen. Esprésase col símbolu ${\displaystyle \cap }$.

Por exemplu:

Dau A={a,e,i,s} y B={a,e,f,h}, si definimos ${\displaystyle C=A\cap B}$, entós C={a,e}.

${\displaystyle C=A\cap B}$

lléese: "el conxuntu C ye neto a la interseición de los conxuntos A y B". Tamién se pue dicir: "C ye'l conxuntu interseición de los conxuntos A y B".

Teoría de conxuntos

Na teoría de conxuntos, la interseición ye una operación binaria nel conxuntu de tolos subconxuntos d'un U, Conxuntu universal, dau. Polo que a cada par de conxuntos A y B de U asóciase-yos otru conxuntu: ${\displaystyle (A\cap B)}$ de U.

Si A y B son dos d'ellos entós la so interseición simbolízase y defínese como:

${\displaystyle A\cap B=\{x\in U\mid \ x\in A\ \land \ x\in B\}}$

La interseición de A y B, ye'l conxuntu d'elementos x de U, talo que, x perteneza a A, y que, x perteneza a B.

Esta operación ye conmutativa, asociativa, tien neutru y tien inversu:

${\displaystyle A\cap B=B\cap A}$

${\displaystyle (A\cap B)\cap C=A\cap (B\cap C)}$

${\displaystyle A\cap \varnothing =\varnothing \cap A=\varnothing }$

${\displaystyle A\cap A^{c}=A^{c}\cap A=\varnothing }$

au:

${\displaystyle A^{c}=\{x\in U\mid x\notin A\}}$ ye'l complementu de A.

Poro, el conxuntu potencia del nuesu universu U y la operación ${\displaystyle \cap }$ ensamen una estructura alxebraica tipu grupu abelianu.

Propiedaes

Seyan A, B y C tres conxuntos cualesquier:

• 1. A ∩ B ⊆ A y A ∩ B ⊆ B.
• 2. A ∩ ∅ = ∅ y A ∩ U = A.
• 3. A ∩ A = A (propiedá idempotente).
• 4. A ∩ B = B ∩ A (propiedá conmutativa).
• 5. (A ∩ B) ∩ C = A ∩ (B ∩ C) (propiedád asociativa).
• 6. a. A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
• 6. b. (B ∪ C) ∩ A = (B ∩ A) ∪ (C ∩ A) (propiedá distributiva respeutu de la xunión).
• 7. A ∪ (A ∩ B) = A = A ∩ (A ∪ B) (llei d'absorción).

Referencies

Enllaces esternos

• Wikimedia Commons tien conteníu multimedia tocante a Interseición de conxuntos.