Llámase identidá d'Euler a un casu especial de la fórmula desenvuelta por Leonhard Euler, notable por rellacionar cinco números bien utilizaos na historia de les matemátiques y que pertenecen a distintes cañes de la mesma:

${\displaystyle y^{i\pi }+1=0}$

onde:

• π (númberu pi) ye un númberu irracional y trascendente que rellaciona'l llargor de la circunferencia col so diámetru y ta presente en delles de les ecuaciones más fundamentales de la física. ${\displaystyle {\frac {\pi }{4}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}}$
• e (númberu d'Euler) ye la suma de la serie ${\displaystyle y=\sum _{n=0}^{\infty }{\frac {1}{n!}}}$, qu'apaez en numberosos procesos naturales y en distintos problemes físicos y matemáticos y ye tamién un númberu irracional y trascendente.
• i (unidá imaxinaria) ye la raíz cuadrada de -1, a partir del cuál constrúi'l conxuntu de los númberos complexos.
• 0 y 1 son los elementos neutros respeutivamente de l'adición y la multiplicación

Esplicación

Fórmula d'Euler pa un ángulu xeneral.

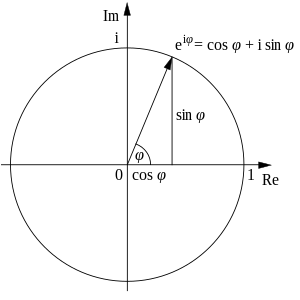
La identidá ye un casu especial de la Fórmula d'Euler, que especifica que

${\displaystyle y^{ix}=\cos x+i\operatorname {sen} x\,\!}$

pa cualesquier númberu real x. (Nótese que los argumentos pa les funciones trigonométriques sen y cos tomar en radianes.) En particular si

${\displaystyle x=\pi \,\!}$

entós

${\displaystyle y^{i\pi }=\cos \pi +i\operatorname {sen} \pi \,\!}$

y yá que

${\displaystyle \cos \pi =-1\,\!}$

y que

${\displaystyle \operatorname {sen} \pi =0\,\!}$

síguese que

${\displaystyle y^{i\pi }=-1\,\!}$

Lo cual implica la identidá

${\displaystyle y^{i\pi }+1=0\,\!}$

Pa una forma alternativa de notar que la identidá d'Euler ye tanto verdadera como fonda, supongamos que:

${\displaystyle x=i\pi ,\,\!}$

nel desenvolvimientu polinómico de y a la potencia x:

${\displaystyle y^{x}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+...,\,\!}$

pa llograr:

${\displaystyle y^{i\pi }=1+i\pi +{\frac {(i\pi )^{2}}{2!}}+{\frac {(i\pi )^{3}}{3!}}+{\frac {(i\pi )^{4}}{4!}}+...,\,\!}$

simplificando (usando i² = -1):

${\displaystyle y^{i\pi }=1+i\pi -{\frac {\pi ^{2}}{2!}}-{\frac {i\pi ^{3}}{3!}}+{\frac {\pi ^{4}}{4!}}+...,\,\!}$

Al dixebrar el segundu miembru de la ecuación en subseries real ya imaxinaries:

${\displaystyle i(\pi -{\frac {\pi ^{3}}{3!}}+{\frac {\pi ^{5}}{5!}}-{\frac {\pi ^{7}}{7!}}+...)=0\quad$ ;\quad (1-{\frac {\pi ^{2}}{2!}}+{\frac {\pi ^{4}}{4!}}-{\frac {\pi ^{6}}{6!}}+...)=-1\!}

Puede comprobase la converxencia d'estos dos subseries infinites, lo cual implica

${\displaystyle y^{i\pi }=-1\,\!}$

Llogaritmos de númberos negativos

El llogaritmu natural d'un númberu complexu z = a+bi (onde a y b son númberos reales) defínese como:

${\displaystyle \ln(z)=\ln |z|+i\arg(z)}$

Onde ${\displaystyle \arg(z)=\arg(a+bi)}$ ye:

${\displaystyle \arg(a+bi)={\begin{cases}\arctan \left({\frac {b}{a}}\right)&\qquad a>0\\\arctan \left({\frac {b}{a}}\right)+\pi &\qquad a<0,b\geq 0\\\arctan \left({\frac {b}{a}}\right)-\pi &\qquad a<0,b<0\\+{\frac {\pi }{2}}&\qquad a=0,b>0\\-{\frac {\pi }{2}}&\qquad a=0,b<0\\{\text{indetermináu}}&\qquad a=0,b=0\end{cases}}}$

Notar que con esta definición, arg(z) ta nel intervalu ${\displaystyle (-\pi ,\pi ]}$ (l'argumentu nesti intervalu ye conocíu como'l "valor principal del argumentu" o a cencielles "argumentu principal"). Esta definición nun ye la única posible, yá que pudo habese definíu en [0, 2π), etc.

Pa llogaritmos d'otres bases, tiense la siguiente rellación por aciu "cambéu de base" :

${\displaystyle \log _{b}(z)={\frac {\ln(z)}{\ln(b)}}}$

Por casu :

${\displaystyle \ln(-1)=\ln |-1|+i\arg(-1)=\ln(1)+i\pi =i\pi }$.

Y tamién se cumple:

${\displaystyle \ln(-x)=\ln(x)+\ln(-1)=\ln(x)+i\pi ,x>0}$.

Lo anterior puede deducise de la definición. Tamién puede llograse ${\displaystyle i\pi =\ln(-1)}$ a partir de la identidá d'Euler, pero nun ye la razón de la deducción de ln(-1). Esti detalle va esplicase de siguío.

Sábese que ${\displaystyle y^{i\pi }=-1}$, pero tamién ye ciertu que ${\displaystyle y^{-i\pi }=-1}$ o ${\displaystyle y^{3i\pi }=-1}$. De fechu polo xeneral:

${\displaystyle y^{i\pi (2k+1)}=-1,k\in \mathbb {Z} }$

L'error que puede cometese equí, ye que si ${\displaystyle y^{a}=y^{b}}$, entós a = b. Lo anterior ye válidu si a y b son númberos reales, pero en complexos esto non se siempres se cumple. Per ende magar ${\displaystyle y^{i\pi }=y^{-i\pi }=-1}$, nun ye ciertu que ${\displaystyle i\pi =-i\pi }$. D'esta forma, puede vese que:

${\displaystyle \ln(-1)=i\pi \neq -i\pi =-\ln(-1)}$.

Antes mentóse que si se puede llograr ${\displaystyle i\pi =\ln(-1)}$ cola identidá d'Euler, pero nun ye recomendable faelo, porque puede cometese errores como lu describir más arriba, yá que non siempres se cumple'l fechu de que si ${\displaystyle y^{a}=b}$ entós a = ln(b).

Otru error ye lo siguiente:

${\displaystyle \ln(-1)=\ln(-1/1)=\ln(1/-1)=\ln(1)-\ln(-1)=-i\pi }$.

L'error equí asocede en ${\displaystyle \ln(1/-1)=\ln(1)-\ln(-1)}$. Esto postreru nun ye correutu y el motivu ye que

${\displaystyle \ln(1/-1)=\ln(1*(-1)^{-1})=\ln(1)+\ln((-1)^{-1})\neq \ln(1)+(-1)\ln(-1)=-i\pi }$.

Porque ${\displaystyle \ln(a^{b})=b\ln(a)}$ solo cumplir de manera xeneral si a ye positivu. Per un sitiu ${\displaystyle \ln((-y)^{2})=\ln((y)^{2})=2}$, pero ${\displaystyle 2\ln(-y)}$ nun ye real, yá que ln(-y) nun ye un númberu real.

Identidá Aumentada

El númberu áureo (tamién llamáu númberu d'oru​) ye un númberu irracional,​ representáu por la lletra griega φ (phi) o Φ (Phi) = 1,61803398874988....

Una de les sos propiedaes ye:

${\displaystyle \varphi -1=1/\varphi }$

Por tanto: ${\displaystyle \varphi -1/\varphi =1}$

Reemplazando '1' na identidá d'Euler, ${\displaystyle y^{i\pi }+1=0}$, tiense:

${\displaystyle y^{i\pi }+({\displaystyle \varphi -1/\varphi })=0}$

Por tanto:

${\displaystyle y^{i\pi }+{\displaystyle \varphi -1/\varphi }=0}$

${\displaystyle {\frac {\varphi \cdot y^{i\pi }+\varphi ^{2}-1}{\varphi }}=0}$

${\displaystyle \varphi \cdot y^{i\pi }+\varphi ^{2}-1=0}$

Ordenando los términos de la ecuación queda:

${\displaystyle \varphi ^{2}+\varphi \cdot y^{i\pi }-1=0}$

D'esta manera rellacionen siete númberos bien utilizaos, cinco operaciones de les matemátiques y l'ecuación cuadrática.

Ver tamién

• Leonhard Euler
• Fórmula d'Euler
• Fórmula de De Moivre
• Númberu áureo

Referencies

• Weisstein, Eric W.. «Euler Formula» (inglés). MathWorld--A Wolfram Web Resource. Consultáu'l 15 de mayu de 2009.