Hipótesis de Riemann
Conxetura y problema matemáticu

Parte real (colloráu) y parte imaxinaria (azul) de la llinia crítica Re(s) = 1/2 de la función zeta de Riemann. Pueden trate los primeros ceros non triviales en Im(s) = ±14,135, ±21,022 y ±25,011.

Un gráficu polar de zeta, esto ye, Re(zeta) vs. Im(zeta), a lo llargo de la llinia crítica s=it+1/2, con t con valores dende 0 a 34.

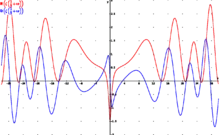
En matemática pura, la hipótesis de Riemann, formulada per primer vegada por Bernhard Riemann en 1859, ye una conxetura sobre la distribución de los ceros de la función zeta de Riemann ζ(s).^[1]

La hipótesis de Riemann, pola so rellación cola distribución de los númberos primos nel conxuntu de los naturales, ye unu de los problemes abiertos más importantes na matemática contemporánea.

L'Institutu Clay de Matemátiques ufiertó un premiu d'un millón de dólares a la primer persona que desenvuelva una demostración correuta de la conxetura.^[2] La mayor parte de la comunidá matemática piensa que la conxetura ye correuta, anque otros grandes matemáticos como J. Y. Littlewood y Atle Selberg amosáronse escépticos, magar l'escepticismu de Selberg foi menguando dende los sos díes de mocedá. Nun artículu en 1989 suxurió qu'un análogu ten de ser ciertu pa una clase muncho más amplia de funciones (la clase de Selberg).

Definición

La función zeta de Riemann ζ(s) ta definida nos númberos complexos como la suma d'una serie infinita de la siguiente forma:

${\displaystyle \zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}={\frac {1}{1^{s}}}+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+\cdots }$

y ye converxente cuando la parte real ye puramente mayor que 1. Leonhard Euler (que morrió 43 años primero que Riemann naciera) demostró qu'esta serie equival al productu de Euler:

${\displaystyle \zeta (s)=\prod _{p{\text{ primu}}}{\frac {1}{1-p^{-s}}}={\frac {1}{1-2^{-s}}}\cdot {\frac {1}{1-3^{-s}}}\cdot {\frac {1}{1-5^{-s}}}\cdot {\frac {1}{1-7^{-s}}}\cdots {\frac {1}{1-p^{-s}}}\cdots }$

onde'l productu infinitu estiéndese sobre'l conxuntu de tolos númberos primos p, y de nuevu converxe pa los complexos s que la so parte real seya mayor que 1. La converxencia del productu de Euler amuesa que ζ(s) nun tien ceros nesta rexón, yá que nengún de los factores tien ceros. La hipótesis de Riemann trata de los ceros fora de la rexón de converxencia de la suma de la serie descrita enantes y del productu de Euler asociáu. Pa caltener el sentíu d'esta hipótesis ye necesariu enllargar analíticamente la función zeta de Riemann ζ(s) de forma que tenga sentíu pa cualquier valor de s. En particular puede espresase por aciu la siguiente ecuación funcional:

${\displaystyle \zeta (s)=2^{s}\pi ^{s-1}\ \operatorname {sen} \left({\frac {\pi s}{2}}\right)\ \Gamma (1-s)\ \zeta (1-s)\!}$

válida pa tolos númberos complexos sacante para s = 1, onde la función tien un polu. Como se dicía enantes, la hipótesis de Riemann trata de los ceros d'esta versión de la función zeta estendida analíticamente. Esta tien ciertos valores, llamaos ceros "triviales", pa los cualos la función zeta anúlase. De la ecuación puede vese que s = −2, s = −4, s = −6, ... (tolos enteros pares negativos) son ceros triviales. Asina mesmu esisten otros valores complexos s, que cumplen la condición 0 < Re(s) < 1, pa los cualos la función zeta tamién s'anula, son los llamaos ceros "non triviales". La conxetura de Riemann fai referencia a estos ceros non triviales afirmando:

Polo tanto los ceros non triviales tendríen d'atopase na llinia crítica s = 1/2 + i t, onde t ye un númberu real y i ye la unidá imaxinaria. La función zeta de Riemann, a lo llargo de la llinia crítica foi estudiada en términos de la función Z, que los sos ceros correspuenden a los ceros de la función zeta sobre la llinia crítica.

Historia

Riemann mentó la conxetura en 1859, que sería llamada la hipótesis de Riemann, na so tesis de doctoráu Sobre los númberos primos menores qu'una magnitú dada, al desenvolver una fórmula esplícita pa calcular la cantidá de primos menores que x. Puesto que nun yera esencial pal propósitu central del so artículu, nun intentó dar una demostración. Él sabía que los ceros non triviales de la función zeta tán distribuyíos en redol a la recta s = 1/2 + i t, y sabía tamién que tolos ceros non triviales teníen de tar nel rangu 0 ≤ Re(s) ≤ 1.^[3]

En 1896, Hadamard y de la Vallée-Poussin probaron independientemente, que nengún cero podía tar sobre la recta Re(s) = 1. Xunto coles otres propiedaes de los ceros non triviales demostraes por Riemann, esto amosó que tolos ceros non triviales tienen de tar nel interior de la banda crítica 0 < Re(s) < 1. Este foi un pasu fundamental pa les primeres demostraciones del teorema de los númberos primos.

En 1900, Hilbert incluyó la hipótesis de Riemann na so famosa llista de los 23 problemes non resueltos — ye parte del problema 8 na llista de Hilbert xunto cola conxetura de Goldbach. Cuando se-y preguntar qué fadría si espertárase dormiendo quinientos años, remarcablemente Hilbert contestó que la so primer entruga sería si la hipótesis de Riemann fuera probada. La hipótesis de Riemann ye l'únicu problema de los que propunxo Hilbert que ta nel premiu del mileniu del Institutu Clay de Matemátiques.

En 1914, Hardy demostró qu'esiste un númberu infinitu de ceros sobre la recta crítica Re(s) = 1/2. Sicasí inda yera posible qu'un númberu infinitu (y posiblemente la mayoría) de los ceros non triviales atópase en dalgún otru llugar sobre la banda crítica. En trabayos posteriores de Hardy y Littlewood en 1921 y de Selberg en 1942 diéronse estimaciones pa la densidá permediu de los ceros sobre la llinia crítica.

Trabayos recién concentráronse nel cálculu esplícitu de la llocalización de grandes cantidaes de ceros (cola esperanza de topar dalgún contraejemplo) y nel establecimientu de cotes cimeres na proporción de ceros que puedan tar lloñe de la llinia crítica (cola esperanza d'amenorgales a cero).

La hipótesis de Riemann y los númberos primos

La formulación tradicional de la hipótesis de Riemann escurez un pocu la importancia real de la conxetura. La función zeta de Riemann tien una fonda conexón colos númberos primos y Helge von Koch demostró en 1901 que la hipótesis de Riemann ye equivalente al considerable refinamientu del teorema de los númberos primos: Esiste una constante C > 0 tal que

${\displaystyle \left|\pi (x)-\int _{2}^{x}{\frac {dt}{\ln(t)}}\right|\leq C\,{\sqrt {x}}\,\ln(x),}$

pa tou x abondo grande, onde π(x) ye la función contadora de primos y ln(x) ye'l llogaritmu natural de x. Lowell Schoenfeld amosó que puede tomase C = 1/(8 π) pa tou x ≥ 2657.

Los ceros de la función zeta y los númberos primus satisfaen ciertes propiedaes de dualidá, conocíes como fórmules esplícites, qu'amuesen, usando analís de Fourier, que los ceros de la función zeta de Riemann pueden interpretase como frecuencies harmóniques na distribución de los númberos primos.

Entá más, si la conxetura de Hilbert-Polya ye cierta, entós cualquier operador que nos dea les partes imaxinaries de los ceros como los sos valores propios tien de satisfaer:

${\displaystyle \sum _{n}y^{-\beta Y_{n}}=\operatorname {tr} [y^{-\beta {\hat {H}}}]=y^{o/2}-y^{-o/2}{\frac {d\psi _{0}}{du}}-{\frac {y^{o/2}}{y^{3o}-y^{o}}},}$

onde tr ye la traza del operador (suma de los sos valores propios), ${\displaystyle \beta \,}$ ye un númberu imaxinariu y ${\displaystyle \psi (x)\,}$ ye la función de Chebyshov que nos suma'l log(x) sobre los primos y les sos potencies enteres, dicha fórmula ye una conclusión de la 'fórmula esplícita' de V. Mangoldt.^[4] Dellos operadores propuestos por C. Perelman, J. Macheca y J. García, paecen acotar los resultaos de la conxetura de Hilbert sobre l'operador, reproduciendo la parte imaxinaria de los ceros.

Cálculu numbéricu

Valor absolutu de la ζ-function.

• Nel añu 2004 Xavier Gourdon verificó la conxetura de Riemann numbéricamente a lo llargo de los primeros diez trillones de ceros non triviales de la función. Sicasí esto nun ye puramente una demostración, numbéricamente ye más interesante atopar un contraejemplo, ye dicir un valor de cero que nun cumpla con que la so parte real ye 1/2, pos esto echaría pelos suelos la validez de la conxetura.

• Hasta'l 2005, l'intentu más seriu pa esplorar los ceros de la función-ζ, ye'l ZetaGrid, un proyeutu de computación distribuyida cola capacidá de verificar billones de ceros per día. El proyeutu acabó n'avientu de 2005, y nengunu de los ceros pudo ser identificáu como contraejemplo de la hipótesis de Riemann.

Ver tamién

• Teorema de los númberos primos
• Función zeta de Riemann
• Función contador de númberos primos
• Fórmula esplícita
• Teoría analítica de númberos

Referencies

Enllaces esternos

• (en) The Riemann Hypothesis in a Nutshell
• (en) Andrew Odlyzko: Tables of zeros of the Riemann zeta function
• (en) Riemann zeros Quantum chaos
• (en) Zetagrid
• (en) Algoritmos pa calcular los ceros de la función de Riemann, por Michael Rubinstein