Función hash

Una función de hash en funcionamientu.

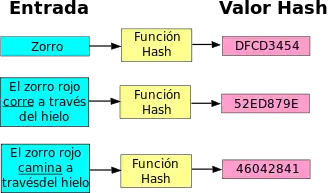
A les funciones resumen tamién se-yos llama funciones hash o funciones digest.^[1]^[2]^[3] Una función hash H ye una función computable por aciu un algoritmu tal que:

$H:O\rightarrow M$

$x\rightarrow h(x)$

Tien como entrada un conxuntu d'elementos, que suelen ser cadenes, y convertir nun rangu de salida finito, de normal cadenes de llargor fixu. Esto ye, la función actúa como una proyeición del conxuntu O sobre'l conxuntu M.

Reparar que M pue ser un conxuntu definíu d'enteros. Nesti casu podemos considerar que'l llargor ye fixa si'l conxuntu ye un rangu de númberos d'enteros yá que podemos considerar que'l llargor fixu ye la del númberu con mayor númberu de cifres. Tolos númberos pueden convertise al númberu especificáu de cifres a cencielles anteponiendo ceros.

De normal el conxuntu O tien un númberu eleváu d'elementos y M ye un conxuntu de cadenes con un númberu más o menos pequeñu de símbolos. La idea básica d'un valor hash ye que sirva como una representación compacta de la cadena d'entrada.

Por esta razón dizse qu'estes funciones resumen datos del conxuntu dominiu.

Oríxenes del términu

El términu hash provién, aparentemente, de l'analoxía col significáu estándar (n'inglés) de dicha pallabra nel mundu real: picar y entemecer. Donald Knuth cree que H. P. Luhn, emplegáu d'IBM, foi'l primeru n'utilizar el conceutu nun memorándum fecháu en xineru de 1953. El so usu masivu nun foi hasta dempués de 10 años.

Terminoloxía acomuñada

Al conxuntu O llámase-y dominiu de la función resumen. A un elementu d'O llámase-y preimagen o dependiendo del contestu clave o mensaxe.

Al conxuntu M llámase-y imaxe de la función hash. A un elementu de M llámase-y valor resumen, códigu hash o a cencielles hash.

Dizse que se produz un choque cuando dos entraes distintes de la función resumen producen la mesma salida. De la definición de función resumen podemos dicir qu'O, el dominiu de la función, puede tener infinitos elementos. Sicasí M, el rangu de la función, tien un númberu finito d'elementos por cuenta de que'l tamañu de les sos cadenes ye fixu. Por tanto la posibilidá d'esistencia de choques ye intrínseca a la definición de función hash. Una bona función resumen ye una que tien pocos choques nel conxuntu esperáu d'entrada. Esto ye, deseyar que la probabilidá de choque seya bien baxa.

Parámetros adicionales

La definición formal dada, dacuando xeneralízase pa poder aprovechar les funciones hash n'otros ámbitos. Pa ello a la función resumen añader nuevos parámetros de forma que'l valor hash nun ye solo función del conteníu en sí, sinón amás d'otros nuevos factores.

Pa topar valores resumen de ficheros dacuando úsense, amás del conteníu en sí, diversos parámetros como'l nome del archivu, el so llargor, hora de creación, etc.

Otres vegaes añaden parámetros que dexen configurar el comportamientu de la función. Por casu, la función resumen puede recibir como parámetru una función de xeneración de valores pseudoaleatorios que ye usada dientro del algoritmu de la función hash.

Otros exemplos de parámetros son l'usu de valores sal, l'usu de claves secretes, l'usu de parámetros qu'especifiquen el rangu de la función (funciones hash de rangu variable), l'usu de parámetros qu'especifiquen el nivel de seguridá que se quier nel valor resumen de salida (funciones hash dinámiques), etc.

Funciones resumen con clave

Una función resumen con clave H_K (n'inglés keyed hash function) ye una función resumen H que tien un parámetru secretu K que pertenez al conxuntu posible de claves ${\mathcal {K}}$ y na que pa una entrada x, h_K(x) ye'l valor resumen de x. Al restu de funciones resumen dizse que son ensin clave (n'inglés unkeyed hash function).

Propiedaes

La calidá d'una función resumen vien definida con base nel prestu de ciertes propiedaes deseables nel contestu nel que se va a usar.

So costu

Calcular el valor hash precisa pocu costu (computacional, de memoria, etc.).

Compresión

Una función hash estrúi dato si puede mapear un dominiu con datos de llargor bien grande a datos con llargor más pequeñu

Uniforme

Dizse qu'una función resumen ye uniforme cuando pa una clave escoyida aleatoriamente ye igualmente probable tener un valor resumen determináu, independientemente de cualesquier otru elementu.

Pa una función hash H uniforme del tipu H:{0,1}^m→{0,1}ⁿ, esto ye:

Les cadenes tán construyíes sobre un alfabetu de 2 símbolos (Alfabetu binariu)
El dominiu ye'l conxuntu de les cadenes de llargor m
El rangu ye'l conxuntu de les cadenes de llargor n

podemos dicir qu'a cada resume correspuénde-y 2^m-n mensaxes y que la probabilidá de que dos mensaxes dean como resultáu la mesma salida ye 2^-n

P'algoritmos de busca, si toles entraes son igualmente probables, búscase esta propiedá pa embrivir el númberu de choques yá que cuantos más choques haya, va ser mayor el tiempu d'execución de les busques.

De rangu variable

En delles funciones resumen el rangu de valores resumen pue ser distintu a lo llargo del tiempu. Exemplu: funciones hash usaes pa tables resumen que precisen espandise. Nestos casos a la función hash tien de pasáse-y un parámetru que-y dexe saber en qué rangu mueve la execución pa topar el valor resumen.

Inyectividad y función hash perfecta

Dizse que la función resumen ye inyectiva cuando cada datu d'entrada se mapea a un valor resumen distintu. Nesti casu dizse que la función resumen ye perfecta. Por que se dea, ye necesariu que la cardinalidad del conxuntu dominiu seya inferior o igual a la cardinalidad del conxuntu imaxe. De normal, namái se dan funciones hash perfectes cuando les entraes tán preestablecidas. Exemplu: mapear los díes del añu en númberos del 1 al 366 según l'orde d'apaición.

Formalización:

$k1\neq k2$ implica $h(k1)\neq h(k2)$

Cuando nun se cumple la propiedá de inyectividad dizse qu'hai choques. Hai un choque cuando $k1\neq k2$ y $h(k1)=h(k2)$ .

Determinista

Una función hash dizse que ye determinista cuando dada una cadena d'entrada siempres devuelve'l mesmu valor hash. Esto ye, el valor hash ye la resultancia d'aplicar un algoritmu qu'opera solu sobre la cadena d'entrada. Exemplos de funciones hash non deterministes son aquelles funciones hash que dependen de parámetros esternos, tales como xeneradores de númberos pseudoaleatorios o la fecha. Tampoco son deterministes aquelles funciones hash que dependen de la direición de memoria na que ta almacenada la cadena d'entrada. Esa direición ye accidental y nun se considera un cambéu de la cadena entrada en sí. De fechu puede camudar dinámicamente mientres la mesma execución del algoritmu de la función hash.

Propiedaes p'analizar la resistencia frente a choques

L'estudiu d'esti tipu de propiedaes ye bien útil nel campu de la criptografía pa los llamaos 'código de detección de cambeos'.

Resistencia a la primera preimagen

^[2]Dizse qu'una función resumen tien resistencia a la primera preimagen o a cencielles que tien resistencia a preimagen (del inglés preimage-resistant) si, dau un valor hash y, ye computacionalmente intratable atopar x tal que h(x)=y.

Resistencia a la segunda preimagen

^[2]Dizse qu'una función resumen tien resistencia a la segunda preimagen (n'inglés second preimage-resistant) si dau un mensaxe x, ye computacionalmente intratable atopar un x', $x\neq x'$ , tal que h(x)=h(x').

Resistencia a choques (CRHF)

^[2]Dizse qu'una función hash tien resistencia a choques o que ye resistente a choques o CRHF (del inglés Collision Resistant Hash Function) si atopar un par $(x,y)$ con $y\neq x$ tal que $h(x)=h(y)$ ye computacionalmente intratable. Esto ye, ye difícil atopar dos entraes que tengan el mesmu valor resumen.

Como atopar una segunda preimagen nun puede ser más fácil qu'atopar un choque, entós la resistencia a choques inclúi la propiedá de resistencia a la segunda preimagen.^[4]^[5] Per otru llau puede dicise que la mayoría de les funciones resumen CRHF son resistentes a preimagen.^[2] La resistencia a choques implica resistencia a preimagen pa funciones hash con salida aleatoria uniforme.^[6]

En dellos trabayos a estes funciones llámase-yos funciones resumen d'un solu sentíu fuertes (del inglés strong one way hash function) pa resaltar que ye fuerte por cuenta de qu'hai llibre eleición de los dos valores x y y.

Función resumen d'un solu sentíu (OWHF)

^[7]Una función hash dizse que ye una función resumen d'un solu sentíu o que ye OWHF (del inglés One-Way Hash Function) si tien les propiedaes de resistencia a preimagen y de resistencia a segunda preimagen. Esto ye, ye difícil atopar una entrada que la so hash seya un valor resumen preespecificado.

Reparar que ye distintu a la definición xeneral que se fai de funciones d'un solu sentíu:

^[2]Una función dizse que ye una función d'un solu sentíu o que ye OWF si pa cada x del dominiu de la función, ye fácil computar f(x), pero pa tou y del rangu de f, ye computacionalmente intratable atopar cualesquier x tal que y=f(x).

La diferencia ente OWHF y OWF ye que OWF nun riquir que seya función resumen nin que seya resistente a segunda preimagen.

En dellos trabayos a estes funciones llámase-yos funciones hash d'un solu sentíu débiles (del inglés weak one way hash function) pa resaltar que ye débil en contraste con CRHF (que ye fuerte) por cuenta de que a los cumplir la propiedá de resistencia a segunda preimagen nun hai llibre eleición na selección del valor x, y por tanto del valor h(x), nel que se tien que producir el choque.

Resistencia al cuasi choque

^[8]H ye resistente al cuasi choque (n'inglés near-colission resistance) si ye difícil atopar dos mensaxes $m$ y $m'$ con $m\neq m'$ pa les cualos les sos imáxenes $H(m)$ y $H(m')$ difieran solamente nunos pocos bits.

^[9]Por casu podemos tener una función resistente a choques de 256 bits que nun ye resistente al cuasi choque porque pueden atopase cuasi-choques pa los 224 bits de más a la izquierda.

Funciones con choques de hash parciales

Son funciones nes qu'invirtiendo ciertu costu en procesamientu de CPU y memoria ye posible atopar en tiempos razonables dos entraes que produzan resultaos nos que los sos bits paecer en ciertu grau. Por casu que se paezan nun porcentaxe de bits, o más comúnmente que sían iguales ye los n-bits más significativos.

Por casu con SHA1 pa consiguir un choque total con fuercia bruto precisaríamos $2^{160}$ comprobaciones o siquier $2^{80}$ usando la paradoxa del cumpleaños. Sicasí si vamos amenorgando'l númberu de bits más significativos que tienen que coincidir, el númberu de comprobaciones va baxando pasu ente pasu.

Funciones resumen con esta propiedá usar en sistemes de prueba de trabayu, como Hashcash o Bitcoin pa consiguir les pruebes de trabayu.

Resistencia a les preimágenes parciales

^[10]Una función resumen tien resistencia a preimágenes parciales (n'inglés Partial-preimage resistance) si ye difícil atopar una parte de la preimagen d'un valor hash inclusive conociendo'l restu de la preimagen. Esto ye, débese recurrir a encomalo bruta: si desconócense t bits de la preimagen, tienen de realizase en permediu 2^n-t operaciones de hash atopalo.

A una función resumen resistente a preimágenes parciales tamién se-y diz que ye llocalmente d'un solu sentíu (del inglés local one-wayness).

Con normalización de datos

En delles aplicaciones, les cadenes d'entrada pueden contener carauterístiques que son irrelevantes cuando comparamos les cadenes. Por casu en delles aplicaciones les mayúscules pueden ser irrelevantes. Por tanto pa topar el valor hash ye interesante inorar les distinciones non relevantes ente les cadenes d'entrada. D'esta forma cadenes distintes con diferencies non relevantes, tienen asociaos valores hash iguales.

Continuidá. Efeuto avalancha

Dizse qu'una función resumen ye continua cuando un cambéu minúsculu (ej un bit) na cadena d'entrada causa pequeños cambeos nel valor hash.

Nuna función resumen dizse que nun hai correlación cuando los bits de les cadenes d'entrada y los bits de les cadenes de salida nun tán rellacionaos, esto ye, cuando un cambéu minúsculu (por casu un bit) na cadena d'entrada causa cambeos nel valor hash comparables a un cambéu de cualesquier otru tipu. Por tanto cualesquier cambéu nel mensaxe orixinal idealmente fai que cada unu de cualesquier bit del valor resumen resultante camude con probabilidá 0.5. Cuando esto asocede (o cuasi) dizse que se produz un efeutu ábanu

En funciones resumen usaes pa busca de normal búsquense funciones tan continues como seya posible; de forma qu'entraes que difieran un pocu tendríen de tener valores hash similares o iguales. Sicasí la continuidá nun ye deseable pa funciones resumen usaes pa sumes de verificación o funciones criptográfiques por evidentes razones.

Resistencia a la computación de nuevos valores hash

^[11]Una función resumen con clave K, $h_{K}(x)$ dizse que tien resistencia a la computación de nuevos valores hash (n'inglés Computation-resistance) si a partir d'un rangu de pares conocíos $(x_{i},h_{K}(x_{i}))$ nun puede ser computáu pa un nuevu datu x $h_{K}(x)$ con $x\neq x_{i}$ pa cualesquier i, ensin que K seya conocida.

Reparar que la propiedá anterior implica que nun tendría de ser posible calcular K a partir d'un rangu de pares conocíos $(x_{i},h_{K}(x_{i}))$ . A esta propiedá llamar propiedá de non recuperación de clave (n'inglés key non-recovery).

L'estudiu d'esti tipu de propiedaes son bien útiles nel campu de la criptografía pa los llamaos códigos de autenticación de mensaxes.

Families de funciones resumen y propiedaes acomuñaes

Motivación^[12]

Podríamos imaxinanos un algoritmu probabilístico de tiempu polinomial con dos mensaxes codificados nel algoritmu que dan llugar a un choque pa una específica función resumen. L'algoritmu a cencielles devolvería los dos mensaxes que causen el choque. Crear tal algoritmu puede ser desaxeradamente difícil, pero una vegada construyíu podría ser executáu en tiempu polinomial. Sicasí, definiendo una familia de funciones resumen como una familia infinita de funciones resumen torga que la busca d'esti algoritmu tenga ésitu pa toles funciones resumen de la familia, porque hai infinites. Por tanto les families resumen apurren un mecanismu interesante pal estudiu y categorización de les funciones resumen al respective de la so fortaleza frente a la busca de choques per parte d'un adversariu. Esti tipu d'estudios ye bien útil nel campu de la criptografía pa los llamaos código de detección de cambeos.

Conceutu

Sía $D=\Sigma \ ^{l}$ , el dominiu de la función, seya $R=\Sigma \ ^{n}$ el rangu de la función. Sía ${\mathcal {K}}$ el conxuntu de toles posibles claves (teóricamente ye infinitu anque na práctica ye finito),

Una familia de funciones hash ${\mathcal {H}}$ ye un conxuntu infinitu de funciones hash de la forma $H:{\mathcal {K}}\times \ D\rightarrow \ R$ (notación equivalente $H_{K}:D\rightarrow \ R)$ , onde cada función de la familia ye indexada por una clave $K\in {\mathcal {K}}$ que cumple les siguientes propiedaes:

${\mathcal {H}}$ ye accesible, ye dicir hai un algoritmu probabilístico de tiempu polinomial, que sobre una entrada $K$ devuelve una instancia $H_{K}$
$D$ ye muestreable, esto ye, hai un algoritmu probabilístico de tiempu polinomial, qu'escueye uniformemente elementos de $D$ .
$H_{K}$ ye computable en tiempu polinomial, esto ye, hai un algoritmu de tiempu polinomial (en l) que sobre una entrada $M\in D$ computa $M\in D$ .

Exemplu: SHA-1 ye una sola instancia de función resumen, non una familia. Sicasí SHA-1 pue ser modificáu pa construyir una familia finita de funciones. M. Bellare y P. Rogaway^[13] modificaron SHA-1 de tala forma que la claves especifica les constantes usaes na cuarta ronda de les funciones. Nesti casu'l tamañu de la clave ye de 128 bits y por tanto ${\mathcal {K}}=\Sigma \ ^{128}$ , $D=\Sigma \ ^{2^{64}}$ y $R=\Sigma \ ^{160*3}$ .

Reparar que na definición d'una función resumen el dominiu puede formalizase como $\Sigma \ ^{*}$ , sicasí nuna función resumen definida como instancia d'un elementu d'una familia de funciones resumen el dominiu ye $\Sigma \ ^{l}$ . Esto ye por cuenta de que por que se cumplan les propiedaes de seguridá ye necesariu que'l dominiu seya muestreado uniformemente en tiempu polinomial. Una familia de funciones ${\mathcal {H}}$ puede siempres ser definida con aquel tamañu apropiáu p'afaer cualquier mensaxe que seya necesariu.

Familia de funciones resumen resistente a choques

De forma informal una familia de funciones ye familia de funciones resumen resistente a choques, tamién llamaes CRHF poles sos sigles n'inglés (Collision Resistant Hash Function), dada una función escoyida aleatoriamente de la familia, un adversariu ye incapaz de llograr un choque pa ella.^[14]

Definición formal

^[15]Dizse qu'una familia de funciones resumen ye una (t,ε)-familia resumen resistente a choques ${\mathcal {H}}$ cola forma ${\mathcal {H}}:\Sigma \ ^{k}\times \;\Sigma \ ^{n}\rightarrow \ \Sigma \ ^{l}$ con n,l y k enteros positivos y n>=l, que satisfaen la siguiente condición: Sía ${\mathcal {F}}$ un buscador de choques de cadenes que pa una entrada K nel espaciu de claves usa tiempu $\leq \;t$ y llogra como salida $\bot \;$ , un par $x,x'\in \Sigma \ ^{n}$ tal que ${\mathcal {H}}_{K}(x)={\mathcal {H}}_{K}(x')$ . Pa cada ${\mathcal {F}}$ ,

Pr_{K}[{\mathcal {F}}({\mathcal {H}})\neq \ \bot \ ]<\epsilon \

.

Reparar que la probabilidá ye tomada sobre les eleiciones aleatories de ${\mathcal {F}}$ .

Mirando esta definición vese que son interesantes aquelles families que tienen un t/ε abondo grande.

Puramente falando falamos de families CRHF pero per simplicidá suelse falar a cencielles de CRHF.

La definición nun se mete en cómo s'escueyen les funciones resumen de la familia. Esti puntu ye crucial.^[16] En realidá, en cualquier aplicación de funciones resumen resistentes a choques, dalguna parte P tienen qu'escoyer una función de la familia de forma aleatoria pa producir la descripción de la función. Ye importante estremar ente dos casos:

La eleición aleatoria puede faese pública (o 'public-coin'). La eleición aleatoria pue ser revelada como parte de la descripción de la función.
La eleición aleatoria tiense que caltener secreta (o 'secret-coin'). La revelación la eleición aleatoria realizada pue que dexe atopar choques. Por tanto P tien que caltener secreta la eleición dempués de producir la descripción de la función.

Evidentemente una familia CRHF elegible de forma pública (public-coin) tamién puede trabayar si unu escueye o caltién la eleición de forma privada (secret-coin).

Función hash universal

Una función resumen universal ye una familia de funciones onde la probabilidá de choque ente dos testos escoyíos ye despreciable.^[17]

Definición formal^[18]

Una k-familia de funciones resumen universal ye un conxuntu H de funciones $h:A\to \;B$ tal que pa cada elementu $x_{1},x_{2},...,x_{k}\in A$ y tolos (non necesariamente distintos) $b_{1},b_{2},...,b_{k}\in B$ .

$Pr_{h\in H}[h(x_{1})=b_{1}\land ...\land h(x_{k})=b_{k}]=|B|^{-k}$

^[19]Una familia de funciones resumen ${\mathcal {H}}$ ye ε-cuasi universal o ε-AU (del inglés ε-almost universal) si ye menor que ε la probabilidá de que dos entraes distintes m,n tengan el mesmu valor resumen acomuñáu, tando la función resumen escoyida aleatoriamente ente los miembros de ${\mathcal {H}}$ . De la definición atalantar# que son interesantes aquelles families que tienen un valor pequeñu de ε indicando que l'adversariu nun puede atopar un par d'entraes que producen el mesmu valor resumen, pa una función resumen escoyida aleatoriamente d'ente los elementos la familia.

Familia de funciones hash universal d'un solu sentíu

Una familia de funciones resumen universal d'un solu sentíu, tamién llamaes UOWHF poles sos sigles n'inglés (Universal One-Way Hash Function), ye una familia de funciones resumen universales onde, escoyida una clave K aleatoriamente nel espaciu de claves, dada una cadena x con valor resumen h_K(x) ye difícil atopar un x' distinta de x tal que h_K(x)=h_K(x'). Al par (x,x') llámase-y par de choque

Definición formal

^[20]^[21]Dizse qu'una familia de funciones resumen ${\mathcal {F'}}$ ye (t,ε)-función resumen universal d'un solu sentíu (UOWHF) si nun esiste nengún adversariu qu'en tiempu menor que t pueda ganar el siguiente xuegu con probabilidá mayor o igual que ε: L'adversariu escueye un valor x del Rangu, entós recibe una clave K del espaciu de claves escoyida de forma aleatoria. El xuegu gana si atopa un x' tal que h_K(x)= h_K(x').

L'adversariu ta compuestu por dos algoritmos ${\mathcal {F'}}=({\mathcal {F'}}_{1},{\mathcal {F'}}_{2})$ .

$F'_{1}$ solo tien como parámetru d'entrada'l conxuntu de la familia de funciones resumen. Produz como salida x y State. x ye'l valor resumen oxetivu y State ye dalguna información extra que puede ayudar a A₂ a atopar el choque.
$F'_{2}$ tien como parámetros d'entrada K,x y State y produz como salida x'

por tanto

Pr_{K}[{\mathcal {F'}}({\mathcal {H}})\neq \ \bot \ ]<\epsilon \

.

siendo $\bot \;$ un par $(x,x')$ con $x\neq x'$ tal que h_K(x)= h_K(x')

Reparar que, al igual que na definición de (t,ε)-CRHF la probabilidá ye tomada sobre les eleiciones aleatories de ${\mathcal {F'}}$ . La gran diferencia ye qu'equí la entrada x afítase primeru.

Mirando esta definición vese que son interesantes aquelles families que tienen un t/ε abondo grande.

Comparanza UOWHF y CRHF^[22]

Una familia UOWHF ye una noción más débil qu'una familia CRHF. Nuna CRHF, al oponente primero dáse-y la clave y dempués ella o él tien que producir la pareya d'entraes que topeta. Atopar choques pa un parámetru fixu d'una UOWHF, pue que seya abondo más fácil, pero esto nun va ayudar a un oponente a violar la seguridá. Simon^[23] demostró qu'esiste un oráculu relativu al cual UOWHF esiste, pero non CRHF.

Funciones hash iteratives. Construcción de Merkle-Damgård

^[24]^[25]^[26]Munches funciones hash construyir por aciu el procesu iterativu siguiente hasta consiguir el valor hash de la entrada X, h(X):

El númberu de bits de la entrada X (en principiu de llargor arbitrariu) tien que ser múltiplu del llargor de bloque. Pa consiguilo tiense una regla de rellenu qu'allarga la entrada a un llargor aceptable. De normal esta regla consiste n'añader a la fin de la entrada unos símbolos adicionales a los que se llama rellenu o padding.
Estrémase la entrada en bloques de llargor fixu. Llogrando un conxuntu de bloques x₁,...,x_t.
Realízase un procesu iterativu de la siguiente forma:

H₀=IV

H_i=f(x_i,H_i-1), i=1,2,...,t y ::h(X)=g(H_t).

Al valor IV llámase-y valor inicial y represéntase por eses sigles pol términu inglés Initial Value. A la función f llamar función de ronda o función de compresión. A la función g llamar tresformamientu de salida. Lo que fai la función g ye derivar a partir de H_t tantos bits como se quieran na salida de la función. Frecuentemente g ye la función identidá o un truncamiento de H_t.

Nesti tipu de descripción de funciones hash hai dos eleiciones importantes que van afectar a les propiedaes que va tener la función:

La eleición de la regla de rellenu. Si lo que se quier ye evitar choques ye recomendable que la regla de rellenu nun dexe qu'esistan dos mensaxes que sían rellenaos al mesmu mensaxe.
La eleición de valor inicial (IV). Tendría De ser definíu como parte de la descripción de la función hash.

A les funciones que se constrúin por aciu l'anterior sistema dizse que son funciones resumen iteratives.

A esta forma de construcción recursiva conocer tamién como de Merkle-Damgård por cuenta de que foi usáu por primer vez por R. Merkle ya I. Damgård independientemente en 1989.

Aplicaciones

Les funciones resumen son usaes en múltiples campos. Exemplos:

Ferramienta básico pa la construcción d'utilidaes más complexes:
- Construcción d'estructures de datos: El so usu en distintes estructures de datos faen más eficientes les busques, y/o dexen asegurar los datos que contienen. Exemplos: tables resumen, árboles de Merkle, llistes resume.
- Construcción d'esquemes de compromisu. Los esquemes de compromisu dexen qu'una entidá escueya un valor ente un conxuntu finito de posibilidaes de tala forma que nun pueda camudala. Esa entidá nun tien que revelar la so eleición hasta si acasu'l momentu final (la eleición puede permanecer oculta).
- Construcción d'algoritmos de cifráu/descifráu. Por casu úsase na construcción de cifradores de fluxu y de cifradores de bloque.
- Construcción d'algoritmos xeneradores de númberos pseudoaleatorios.
- Construcción de cadenes pseudoaleatorias. Por casu el llamáu modelu d'oráculu aleatoriu basar en considerar que funciones hash con ciertes propiedaes pórtense como funciones qu'escueyen cadenes al azar, usar pal estudiu de la seguridá los esquemes criptográficos.
- Construcción d'algoritmos de testeo de pertenencia o non a un conxuntu.- Usáronse funciones hash pa la construcción d'acumuladores criptográficos y filtros de Bloom. Estes teunoloxíes dexen establecer mecanismos que dexen pronunciase, dacuando con ciertu grau d'error, sobre la pertenencia o non a ciertu conxuntu.
- Construcción de métodos de xeneración de sellos de tiempu confiables.
Ferramienta pa protexer la integridá
- Na firma dixital
  - Como dato que se robla: nos algoritmos de firma convencionales de normal en llugar de roblar tol conteníu suelse ser roblar solo'l valor hash del mesmu. Dalgunes de les motivaciones pa faer esto son:^[27]
    - Cuando s'usa pa roblar algoritmos de firma por bloques onde los mensaxes son más llargos que'l bloque, nun ye seguro roblar mensaje bloque a bloque yá que un enemigu podría borrar bloques del mensaxe robláu o inxertar bloques de la so eleición nel mensaxe primero que seya robláu. Al usar una función hash faemos un tresformamientu que fai a la firma dependiente de toles partes del mensaxe.
    - De normal los valores hash son muncho más curtios que los datos orixinales d'entrada. Puede ameyorase enforma la velocidá de firma roblando'l valor hash en llugar de roblar el datu orixinal.
    - Si los mensaxes a roblar pueden tener cierta estructura alxebraica y l'algoritmu de firma pórtase de forma que'l sistema resultante pue ser vulnerable a criptoanálisis con ataques de testu escoyíu, podemos usar funciones hash pa destruyir esta estructura alxebraica.
  - Como parte del algoritmu de firma: desenvolviéronse algoritmos de firma qu'usen funciones hash n'el mesmu algoritmu de firma como una ferramienta interno del mesmu. Exemplu d'esti tipu algoritmos son l'esquema de firma de Merkle.
- Suma de verificación (del inglés checksum): cuando quier almacenase o tresmitir información, pa protexer frente a errores casuales nel almacenamientu o tresmisión, ye útil acompañar a los datos de valores hash llograos a partir d'ellos aplicando funciones hash con ciertes propiedaes de forma que puedan ser usaos pa verificar hasta ciertu puntu'l mesmu datu. Al valor hash llámase-y Suma de verificación.
- Prueba de la integridá de conteníos: por casu, cuando se distribúi un conteníu pola rede, y quier tase seguru de que lo que-y llega al receptor ye lo que se ta emitiendo, apúrrese un valor resume del conteníu de forma que esi valor tien que llograse al aplicar la función resume sobre'l conteníu distribuyíu asegurando asina la integridá. A esto suélse-y llamar checksum criptográficu por cuenta de que ye un checksum que rique l'usu de funciones resume criptográfiques por que seya difícil xenerar otros ficheros falsu que tengan el mesmu valor resume. Otru exemplu d'usu esta teunoloxía pa verificar la integridá ye calcular y guardar el valor resume d'archivos pa poder verificar darréu que naide (Ej un virus) modificar. Si en llugar de verificar la integridá d'un solu conteníu lo que se quier ye verificar la integridá d'un conxuntu d'elementos, pueden usase algoritmos basaos en funciones resumen como los árboles de Merkle que se basen n'aplicar reiteradamente les funciones resumen sobre los elementos del conxuntu y sobre los valores resumen resultantes.
Ferramientes venceyaes a l'autenticación y control d'accesu
- Autenticación d'entidaes: por casu, ye frecuente l'usu pa esti propósitu de funciones resumen deterministes con clave secreta que tienen ciertes propiedaes (Códigos de autenticación de mensaxes). Nestos esquemes tanto'l serviciu de autenticación, o verificador, como la entidá que se quier autenticar caltienen de callao la clave de la función resumen. L'esquema funciona de la siguiente forma: El que se quier autenticar xenera un mensaxe y calcula el so valor resumen. Estos dos datos mandar al verificador. El verificador comprueba que'l valor resumen corresponder col mensaxe unviáu y de esta forma verifica que la entidá tien la clave secreta y per otra parte puede asegurar que'l mensaxe ye íntegru (nun foi modificáu desque se calculó'l valor resumen). Reparar que l'esquema nun tien la propiedá del nun refugo per parte del que se quier autenticar una y bones el verificador, al disponer de la clave secreta, puede xenerar tamién los valores resumen.
- Proteición de claves: pa comprobar la correición d'una clave nun ye necesariu tener la clave almacenada, lo que puede ser aprovecháu por que daquién non autorizáu apuerte a ella, sinón almacenar el valor resumen resultante d'aplicar una función resumen determinista. D'esta forma pa verificar si una clave ye correuta basta con aplicar la función resumen y verificar si la resultancia coincide col que tenemos almacenáu. Si amás queremos que la contraseña seya d'un solu usu podemos usar cadenes de resume como en S/KEY
- Derivación de claves: por casu, en delles aplicaciones usen funciones resumen pa derivar una clave de sesión a partir d'un númberu de transaición y una clave maestra. Otru exemplu d'aplicación sería l'usu de funciones resumen pa consiguir sistemes d'autenticación con claves d'un solu usu o OTP (del inglés One Time Password). Nesti tipu de sistemes la clave ye válida pa un solu usu. Estos sistemes basar en tener una grana inicial y depués dir xenerando claves (por aciu un algoritmu que puede usar funciones resumen) que pueden tener un solu usu y asina evitar ataques de REPLAY.
Ferramienta pa la identificación y la rápida comparanza de datos: Pueden usase funciones hash p'apurrir una identificación d'oxetos o situaciones. Una bona función hash pa esti propósitu tendría de ser rápida y asegurase de que dos oxetos o situaciones que se considerar iguales dean llugar al mesmu valor hash. Reparar que dos oxetos o situaciones pueden ser consideraos iguales ensin ser idénticos. Por casu podemos considerar iguales a dos ficheros que son distintos bit a bit porque realmente son la digitalización de la mesma película. Ye llabor del diseñu de la función hash prindar la esencia del criteriu d'igualdá. Per otra parte la evaluación de la función hash tendría de ser pocu costosa pa facilitar la rápida comparanza d'elementos candidatos a ser iguales y de esta forma poder implementar algoritmos de busca rápidos.
- Buelgues dixitales: l'usu de funciones hash aplicaos a cadenes dexen llograr valores hash que pueden usase detectar fácilmente l'apaición d'esos datos en distintos sitios. Pueden ser usaos pa distintos usos como busca de virus, autenticación con datos biométricos, detección de copies, etc. La idea puede usase más allá de testos y ser aplicáu a cualquier tipu de conteníu multimedia:^[28]^[29] Les funciones hash específicamente diseñaes pa esti propósitu llogren valores hash que dexen detectar carauterístiques intrínseques del conteníu multimedia, de forma que pueda identificase si dos archivos distintos corresponder col mesmu conteníu multimedia. Como aplicación práctica d'esti tipu d'algoritmu tenemos los programes que s'executen en dispositivos móviles y que son capaces d'aldovinar el títulu del cantar que ta sonando na habitación solamente prindando'l soníu y comparándolo con estos valores hash. Esti tipu d'algoritmos tamién puede utilizase pa proteición de conteníos multimedia yá que dexa validar automáticamente si ciertu fichero multimedia ta protexíu o non por derechos d'autor.
- Identificación de conteníos: en delles aplicaciones usa'l valor hash d'un conteníu multimedia pa identificar esi conteníu independientemente del so nome o allugamientu. Esto ye llargamente usáu en redes Peer-to-peer qu'intercambien d'archivos, tales como Kazaa, Ares Galaxy, Overnet, BitTorrent.
- Identificar un rexistru nuna base de datos y dexar con ello un accesu más rápidu a los rexistros (inclusive más rápidu que teniendo índices).
- Algorítmos de busca de subcadenas: los algoritmos de busca de subcadenas traten el problema de buscar subcadenas, a la que llamen patrón, dientro d'otra cadena a la que llamen testu. Hai algoritmos d'esti tipu qu'usen funciones hash nel so implementación. Exemplu: algoritmu Karp-Rabin.
- Detección de virus: Pa detectar los virus munchos antivirus definen funciones hash que prinden la esencia del virus y que dexen estremalos d'otros programes o virus. Ye lo que se llama firma del virus. Estes firmes son usaes polos antivirus pa poder detectalos.

Munches de les aplicaciones de les funciones hash son relatives al campu de la criptografía ( Cifradores, acumuladores criptográficos, firma dixital, protocolos criptográficos de autenticación, etc.). La criptografía ye una caña de les matemátiques qu'apurre ferramientes pa consiguir seguridá nos sistemes d'información. Les funciones resumen interesantes nel área de la criptografía carauterizar por cumplir una serie de propiedaes que dexen a les utilidaes criptográfiques que les utilicen ser resistente frente ataques qu'intenten frayar la seguridá del sistema. A les funciones hash que cumplen estes propiedaes se les llapada funciones hash criptográfiques.

Ver tamién

Función hash criptográfica
Códigu de detección de cambeos
Códigu de autenticación de mensaxes

Referencies

↑ H. Tiwari, K. Asawa "Cryptographic Hash Function: An Elevated View", European Journal of Scientific Research, 2010
1 2 3 4 5 6 A. J. Menezes et all, "Handbook of Applied Cryptography", CRC Press 2011
↑ D. Henrici,"Concepts, Protocols, And Architectures". Lectures Notes in Electrical Engineering. Springer-Verlag 2008.
↑ Bart Preneel,"The State of Cryptographic Hash functions.
↑ I. B. Damgard, "Collision free hash functions and public key signatures schemes". Advances in Cryptology- Crypto'89. LNCS 304 pages 203-216. Springer 1987
↑ Kazumaro Aoki, Yu Sasaki, "Meet in the midle preimage attacks against reduced SHA-0 and SHA-1"
↑ H. Tiwari et all, "Cryptographic Hash Function:An elevated View", European Jorunal of Scientific Research, Vol 43 páxs.452-465. 2010
↑ W. R. Speirs,"Dynamic cryptographic hash functions", Thesis. Purdue University School.2007
↑ Peter Stavroulakis et all,"Handbook of Information and Communication Security", Spring 2010
↑ Dirk Henric,"RFID security and privacy: concepts, protocols, and architectures", Springer 2008
↑ Günter Schäfer,"Security in fixed and wireless networks: an introduction to securing data communications". Willey 2003
↑ William Speirs, "Dynamic cryptographic hash functions"
↑ Mihir Bellare and Phillip Rogaway. "Introduction to modern cryptography. Chapter 5.September 2005.
↑ Chum-Yuan Hsiao et all, "Finding Collision on a Public Road, or Do Secure Hash Functions Need Secret Coins?"
↑ "Signature Scheme in Multi-User Setting", The Institute of Electronics, Information and Communication Engineers, 2006
↑ Chun-Yuan Hsiao et all, "Finding Collisions on a Public Road, or Do Secure Hash Functions Need Secret Coins
↑ Mridul Nandi,"A Generic Method to Extend Message Space of a Strong Pseudorandom Permutation"
↑ A. R. Caldebank et all, "Improved Range Summable Random Variable Construction Algorithms", Proceedings of the 16 Annual ACM-SIAM Symposium on Discrete Algorithms
↑ Ted Krovetz,"Message Authentication on 64-Bit Architectures", Selected Areas in Cryptography, LNCS 4356, Springer.2006.
↑ Ilya Mironov,"Collision-Resistant No More: Hash-and-Sign Paradigm Revisited", Public Key Cryptography PKC 2006, LNCS 3958. Springer 2006
↑ D. Hong et all, "Higher Order Universal One-Way Hash Functions",Center for Information Security Technologies, Korea University, Seoul,Korea.
↑ Henk C. A. Van Tilborg,"Encyclopedia of Cryptography and Security" Second Edition. pg 1349. Springer 2011
↑ D. Simon, "Finding collisions on a one-way street:Can secure hash functions be based on xeneral assumptions?, EUROCRYPT 98 pp 334-345, 1998
↑ H. Tiwari,"Cryptographic Hash Function: An Elevated View", European journal of Scientific Research, Vol 43 páxs.452-465.2010
↑ Bart Preneel,"Cryptographic Primitives for Information Authentication-State of the Art", Katholieke Universiteit Leuven, COSIC'97 LNCS 1528 1998
↑ Chris Mitchell,"Developments in Security Mechanism Standards", "Internet and Intranet Security Management: Risks and Solutions", editáu por L. Janczewski,Idea Group Publishing.2000
↑ Ivan Bjerre Damgård, "Collision free hash functions and public key signature schemes",Advances in Cryptology - EUROCRYPT'87, Lncs 304 PP 203-216. Springer-Verlag Berlin Heidelberg 1988
↑ P. Cano et all. A Review of Audiu Fingerprinting Journal of VLSI Signal Processing 41, 271–284, 2005
↑ Loubna Bouarfa. Research Assignment on Videu Fingerprinting Faculty of Electrical Engineering, Mathematics and Computer Science Delft University of Technology

Enllaces esternos

Funciones hash pa busca en tables hash (n'inglés).
Xenerador de resúmenes: xenerador en llinia de hashes (CRC, MD2, MD4, MD5, SHA1, Tiger, Snefru, RipeMD, Whirlpool, Haval, ente otros). Aproximao 123 algoritmos y 200 maneres (Hex, Base64).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] H. Tiwari, K. Asawa "Cryptographic Hash Function: An Elevated View", European Journal of Scientific Research, 2010

[cacr.math.uwaterloo_1-2] 1 2 3 4 5 6 A. J. Menezes et all, "Handbook of Applied Cryptography", CRC Press 2011

[3] D. Henrici,"Concepts, Protocols, And Architectures". Lectures Notes in Electrical Engineering. Springer-Verlag 2008.

[4] Bart Preneel,"The State of Cryptographic Hash functions.

[5] I. B. Damgard, "Collision free hash functions and public key signatures schemes". Advances in Cryptology- Crypto'89. LNCS 304 pages 203-216. Springer 1987

[6] Kazumaro Aoki, Yu Sasaki, "Meet in the midle preimage attacks against reduced SHA-0 and SHA-1"

[7] H. Tiwari et all, "Cryptographic Hash Function:An elevated View", European Jorunal of Scientific Research, Vol 43 páxs.452-465. 2010

[8] W. R. Speirs,"Dynamic cryptographic hash functions", Thesis. Purdue University School.2007

[9] Peter Stavroulakis et all,"Handbook of Information and Communication Security", Spring 2010

[10] Dirk Henric,"RFID security and privacy: concepts, protocols, and architectures", Springer 2008

[11] Günter Schäfer,"Security in fixed and wireless networks: an introduction to securing data communications". Willey 2003

[12] William Speirs, "Dynamic cryptographic hash functions"

[13] Mihir Bellare and Phillip Rogaway. "Introduction to modern cryptography. Chapter 5.September 2005.

[14] Chum-Yuan Hsiao et all, "Finding Collision on a Public Road, or Do Secure Hash Functions Need Secret Coins?"

[15] "Signature Scheme in Multi-User Setting", The Institute of Electronics, Information and Communication Engineers, 2006

[16] Chun-Yuan Hsiao et all, "Finding Collisions on a Public Road, or Do Secure Hash Functions Need Secret Coins

[17] Mridul Nandi,"A Generic Method to Extend Message Space of a Strong Pseudorandom Permutation"

[18] A. R. Caldebank et all, "Improved Range Summable Random Variable Construction Algorithms", Proceedings of the 16 Annual ACM-SIAM Symposium on Discrete Algorithms

[19] Ted Krovetz,"Message Authentication on 64-Bit Architectures", Selected Areas in Cryptography, LNCS 4356, Springer.2006.

[20] Ilya Mironov,"Collision-Resistant No More: Hash-and-Sign Paradigm Revisited", Public Key Cryptography PKC 2006, LNCS 3958. Springer 2006

[21] D. Hong et all, "Higher Order Universal One-Way Hash Functions",Center for Information Security Technologies, Korea University, Seoul,Korea.

[22] Henk C. A. Van Tilborg,"Encyclopedia of Cryptography and Security" Second Edition. pg 1349. Springer 2011

[23] D. Simon, "Finding collisions on a one-way street:Can secure hash functions be based on xeneral assumptions?, EUROCRYPT 98 pp 334-345, 1998

[24] H. Tiwari,"Cryptographic Hash Function: An Elevated View", European journal of Scientific Research, Vol 43 páxs.452-465.2010

[25] Bart Preneel,"Cryptographic Primitives for Information Authentication-State of the Art", Katholieke Universiteit Leuven, COSIC'97 LNCS 1528 1998

[26] Chris Mitchell,"Developments in Security Mechanism Standards", "Internet and Intranet Security Management: Risks and Solutions", editáu por L. Janczewski,Idea Group Publishing.2000

[27] Ivan Bjerre Damgård, "Collision free hash functions and public key signature schemes",Advances in Cryptology - EUROCRYPT'87, Lncs 304 PP 203-216. Springer-Verlag Berlin Heidelberg 1988

[28] P. Cano et all. A Review of Audiu Fingerprinting Journal of VLSI Signal Processing 41, 271–284, 2005

[29] Loubna Bouarfa. Research Assignment on Videu Fingerprinting Faculty of Electrical Engineering, Mathematics and Computer Science Delft University of Technology

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

Oríxenes del términu

Terminoloxía acomuñada

Parámetros adicionales

Funciones resumen con clave

Propiedaes

So costu

Compresión

Uniforme

De rangu variable

Inyectividad y función hash perfecta

Determinista

Propiedaes p'analizar la resistencia frente a choques

Resistencia a la primera preimagen

Resistencia a la segunda preimagen

Resistencia a choques (CRHF)

Función resumen d'un solu sentíu (OWHF)

Resistencia al cuasi choque

Funciones con choques de hash parciales

Resistencia a les preimágenes parciales

Con normalización de datos

Continuidá. Efeuto avalancha

Resistencia a la computación de nuevos valores hash

Families de funciones resumen y propiedaes acomuñaes

Motivación[12]

Conceutu

Familia de funciones resumen resistente a choques

Definición formal

Función hash universal

Definición formal[18]

Familia de funciones hash universal d'un solu sentíu

Definición formal

Comparanza UOWHF y CRHF[22]

Funciones hash iteratives. Construcción de Merkle-Damgård

Aplicaciones

Ver tamién

Referencies

Enllaces esternos

Motivación^[12]

Definición formal^[18]

Comparanza UOWHF y CRHF^[22]