Física del estáu sólidu
rama de la física
física

La física del estáu sólidu ye la caña de la Física de la materia entestada que trata sobre l'estudiu de los sólidos, esto ye, la materia ríxida o semirrígida. Estudia les propiedaes físiques de los materiales sólidos, utilizando disciplines tales como la mecánica cuántica, la cristalografía, l'electromagnetismu y la metalurxa física. Forma la base teórica de la ciencia de materiales y el so desenvolvimientu foi fundamental nel campu de les aplicaciones teunolóxiques de microelectrónica al faer posible el desenvolvimientu de transistores y materiales semiconductores.*

La mayor parte de la investigación na teoría de la física d'estáu sólidu centrar nos cristales, en gran parte porque la periodicidad de los átomos nun cristal, la so carauterística definitoria, facilita'l modeláu matemáticu, y tamién porque los materiales cristalinos tienen de cutiu carauterístiques llétriques, magnétiques, óptiques, o mecániques que pueden ser esplotaes pa los propósitos de la inxeniería.

El marcu de la mayoría de la teoría na física d'estáu sólidu ye la formulación (de la onda) de Schrödinger de la mecánica cuántica non relativista. Un importante puntu de partida pa enforma analís ye'l teorema de Bloch, que caracteriza les funciones d'onda d'electrones nun potencial periódicu. Puesto que el teorema de Bloch aplícase solamente a los potenciales periódicos, y yá que los incesantes movimientos al azar de los átomos nun cristal atayen la periodicidad, esti usu del teorema de Bloch ye solamente un aproximamientu, pero demostró ser un aproximamientu descomanadamente pervalible, ensin la cual la mayoría del analís de la física d'estáu sólidu seríen insuperables. Les esviaciones de la periodicidad son trataes pola teoría de perturbaciones de la mecánica cuántica.

Introducción

Los cuerpos sólidos tán formaos por átomos densamente empaquetados con intenses fuercies d'interacción ente ellos. Los efeutos d'interacción son responsables de les propiedaes mecániques, térmiques, llétriques,magnétiques y óptiques de los sólidos.

Una carauterística importante de la mayoría de los sólidos ye'l so estructura cristalina. Los átomos tán distribuyíos en posiciones regulares que se repiten regularmente de manera xeométrica. La distribución específica de los átomos puede debese a una variada gama de fuercies. Por casu, dellos sólidos como'l cloruru de sodiu o sal común caltiénense xuníos por enllaces iónicos debíos a la interacción electrostática ente los iones que componen el material. N'otros, como'l diamante, los átomos comparten electrones, lo que da llugar a los llamaos enllaces covalentes.

Les sustancies inertes, como'l neón, nun presenten nengunu d'esos enllaces. La so esistencia ye la resultancia d'unes fuercies d'atraición conocíes como fuercies de Van der Waals, asina llamaes n'honor al físicu holandés Johannes Diderik van der Waals. Estes fuercies apaecen ente átomos neutros o molécules como resultáu de la polarización llétrica. Los metales, caltiénense xuníos polo que se conoz como gas electrónico, formáu por electrones llibres de la capa atómica esterna compartíos por tolos átomos del metal y que definen la mayoría de les sos propiedaes. tamién presenta carauterístiques del estáu sólidu tales como:

Estructura cristalina

La física del estáu sólidu constitúi una parte importante de la física cuántica. Cola so ayuda podemos entender les propiedaes mecániques, térmiques, llétricu-magnétiques y óptiques propies de los sólidos.

La esistencia de la materia nun estáu o otru depende de les condiciones de presión y temperatura nes que se formaron. De la mesma forma, estos parámetros condicionen la formación de la estructura interna del sólidu.

Cada elementu tien les sos propies curves de cambéu de fase, de manera que dependiendo del elementu precisarán unes condiciones o otres pa la formación del sólidu o pa realizar cualesquier otru cambéu de fase. Dependiendo del algame del orde espacial de la estructura interna na materia y la so distribución na mesma podemos estremar ente:

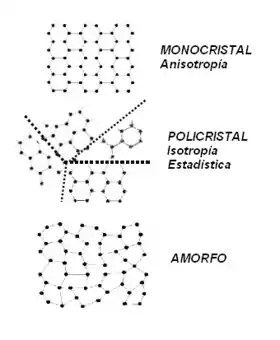
• Monu cristal: Presenta una fuerte interacción ente los sos componentes los cualos describen una mínima oscilación con poca enerxía potencial. Les partícules tán dispuestes d'alcuerdu a un orde nel espaciu que ta determináu acordies con una rede estructural formada pola "recreación" xeométrica de l'alviola unidá en tola estructura del sólidu. Presenten lo que se conoz como Anisotropía.

• Poli cristal: Ta compuestu por diversu rexones nes qu'individualmente se recrea un monocristal anque les disposiciones de caúna d'estes rexones nun son simétriques ente sigo. Presenta lo que se llama Isotropía estadística.

• Amorfos: Nun presenten una estructura o distribución nel espaciu, lo cual determinar como una estructura espacial tridimensional ensin definir. Nun se trata d'una estructura cristalina.

Formes y propiedaes del cristal.

En cierto, esta clasificación namái ye aplicable a sustancies pures.

Nun modelu de sólidu nel que los átomos tán coneutaos ente sigo por aciu una especie de "muelles" (los cualos representaríen la enerxía potencial que los xune), la enerxía interna del sólidu componer d'enerxía potencial elástica y enerxía cinética de les sos átomos. La presión ye una midida del grau de compresión de los sos átomos y la temperatura una midida de la enerxía cinética interna del conxuntu de los mesmos. Esto déxanos determinar qu'acordies coles carauterístiques esternes del mediu en que s'atope, van dexar al elementu en cuestión poder adoptar un estáu o otru ya inclusive formar o non una estructura cristalina.

Sicasí la formación d'una estructura cristalina nun ye un procesu fixu nun mesmu elementu, yá que inclusive tratándose asina les condiciones de formación del sólidu podríen determinar dos estructures cristalines distintes pa un mesmu elementu, la cuál da les propiedaes tantu físiques y llétriques como óptiques al nuevu sólidu formáu. Por casu, el carbonu puede cristalizar en grafitu en determinaes condiciones y n'otres cristaliza nel diamante, ensin dulda les carauterístiques d'unu frente a otru difieren abondo pa tratase en dambos casos de carbonu cristalizáu.

Esti procesu non yá ye dependiente de la presión y la temperatura en sí mesmos, sinón tamién del tiempu aplicáu en cada unu de dichos factores. D'esta forma sábese que la formación de cristales rique un calentamientu del material a alta temperatura, aproximao 200 °C, lo que se conoz como temperatura de cristalización, a partir de la cual l'elementu fundir pa darréu, dempués d'un tiempu lo suficientemente llargu, cristalice. Al añader temperatura al material, realmente támos-y damos enerxía, dexando que les partícules que la componen bazcuyen a mayor velocidá con una mayor enerxía térmica, llogrando que se funda(camude al estáu líquidu). Depués por aciu un enfriamientu lentu consiguimos avagar les partícules que, de forma natural, tienden a retomar una forma xeométrico y ordenao na rede interna consiguiendo asina que se forme un cristal.

Otramiente, si repitimos el procesu pero aplicando un tiempu d'enfriamientu demasiáu curtiu torgamos que les partícules pueda "re-asitiase" nuna rede cristalina homoxénea faciendo asina que la solidificación de llugar a un amorfu.

El policristal ye'l casu más típicu de los que puedan atopase na naturaleza, una y bones un monocristal ye un casu qu'escasamente se da. Un cristal tien distintes zones que nun pueden homogeneizarse ente si, pero puede faese que sían como monocristales individuales en caúna de les sos rexones.

Siguiendo l'exemplu del carbonu, la cualidá de qu'un mesmu elementu pueda cristalizar en distintes formes llévanos al fechu de que ye la rede cristalina que formen la que determina les sos propiedaes. Na naturaleza esisten 14 tipos de redes cristalines (otres más complexes son combinaciones d'estes más simples) que son conocíes como Redes de Bravais.

Estes redes son organizaciones xeométriques tridimensionales nel espaciu carauterístiques de les partícules del sólidu. Asina pueden estudiase les distribuciones na rede de los elementos.

Por casu: El fósforu(P) cristaliza nuna estructura cúbica, el fierro (Fe) nuna bcc ("Body Center Cubic") y la plata (Ag) nuna fcc ("Face Center Cubic"). Otros cristalicen en redes compuestes como por casu los elementos del grupu IV(C, Si, Gue...) o del III de la tabla periódica que lo faen nuna estructura de tipu diamante, que ye la combinación de dos red fcc con una distancia interatómica de 1/4 de la diagonal.

Representación d'una alviola na disposición xeométrica de les sos partícules.

Según caúna d'estes distribuciones, caúna de les partícules asitiaes nos nodos de la estructura, contribúi nuna parte a la formación del númberu d'átomos conteníu nel so interior. Trátase del númberu de partícules por alviola elemental que puede llograse como:

${\displaystyle nc={\frac {nv}{8}}+nin+{\frac {nf}{2}}}$

Siendo "nv" el númberu de partícules nos vértices, "nin" nel interior y "nf" nes cares del tetraedru.

Por cuenta de que munchos de los compuestos elementales presenten simetría esférica podemos visualizales considerando éstes como empaquetamientos espaciales d'esferes ríxides. Partiendo d'esta idea, podemos determinar la llamada Fracción de Empaquetamiento que nos apurre una midida de lo "llena" que ta la estructura reticular:

${\displaystyle fc={\frac {n_{c}\cdot V_{y}}{a^{3}}}={\frac {Volume.de.les.esferes}{Volumen.de.la.celda}}}$

Pa reparar la estructura interna que tien un cristal xeneralmente puede determinase a partir del analís de la difracción ondulatoria producida cuando los fotones inciden nel cristal.

Gracies a estes observaciones W.L.Bragg propunxo la conocida Llei de Bragg, que dexa ver superficialmente la posición de los planos que formen los átomos.. Llei de Bragg:

${\displaystyle n\lambda =2d\sin(\theta )\,}$

Estes mesmes propiedaes pertenecientes a los sólidos cristalinos y el fundamentu de los cambeos de fase ye l'utilizáu nel procesu de grabación de CD-RW y DVD-RW por aciu cambeos na estructura cristalina, faciendo zones amorfes o policristalinas, según los datos (bits) que se deseyen grabar. Otres propiedaes y teoríes tán rellacionaes cola física de los cristales como les bandes d'enerxíes o los modelos qu'espliquen les propiedaes llétriques de conductores metálicos y semiconductores.

Ver tamién: Teoría de bandes

Modelu de bandes enerxétiques

El comportamientu de los electrones ta rexíu poles lleis de la mecánica cuántica, polo tanto:

• Los electrones nun pueden tener cualquier nivel d'enerxía: los estaos d'enerxía tán cuantificados. A un conxuntu de niveles d'enerxía mui cerca ente sigo denominar banda d'enerxía y considerar continua.
• Non toles bandes ocúpense uniformemente, sinón que dalgunes tienen más probabilidaes de ser ocupaes qu'otres, inclusive hai bandes totalmente sacupaes, esto ye que la probabilidá de qu'un electrón tenga esi nivel d'enerxía ye nula o bien cercana a cero.

Modelu de los enllaces covalentes

Plantía:Recordatoriu El modelu de Drude dexaba esplicar el comportamientu como conductor de dellos sólidos basándose na aplicación de la teoría cinética a los electrones nun sólidu. Sicasí esti modelu yera insuficiente a la d'esplicar el comportamientu d'otros materiales que güei día se conocen como semiconductores. En respuesta al modelu de Drude surdió'l modelu de bandes enerxétiques, que basándose nes distribuciones de los electrones nos sos orbitales a manera de rexones discretes, puede esplicar el comportamientu de la conductividá nos materiales.

Usualmente, preséntase esti esquema basáu nel modelu atómicu de Bohr y el principiu d'esclusión de Pauli.

Supóngase una rede cristalina formada por átomos de siliciu. Cuando los átomos tán aisllaos, l'orbital s (2 estaos con dos electrones) y l'orbital p (6 estaos con 2 electrones y cuatro vacantes) van tener una cierta enerxía Y_s y Y_p respeutivamente (puntu A). A midida que mengua la distancia interatómica empieza a reparase la interacción mutua ente los átomos, hasta que dambos orbitales lleguen a formar, pola distorsión creada, un sistema electrónicu únicu. Nesti momentu tiénense 8 orbitales híbridos sp³ con cuatro electrones y cuatro vacantes (puntu B).

Si sigue menguándose la distancia interatómica hasta la configuración del cristal, empiecen a interferir los electrones de les capes internes de los átomos, formándose bandes d'enerxía (puntu C). Los trés bandes de valores que pueden estremase son:

1. Banda de valencia. 4 estaos, con 4 electrones.
2. Banda prohibida. Nun puede haber electrones con esos valores d'enerxía nel cristal.
3. Banda de conducción. 4 estaos, ensin electrones.

Conductividá llétrica

La conducción llétrica nun sólidu preséntase cuando'l mesmu tien parcialmente enllena la so banda de conducción. Tamién hai conducción llétrica cuando la banda de conducción ta vacida y amás ésta se traslapa cola banda de valencia.

Temes de la física d'estáu sólidu

• Electrónica d'estáu sólidu
• Sólidu amorfu
• Estructura cristalina
  • Defectu cristalín
  • Cuasicristal
  • Modelu d'electrón llibre
  • Rede recíproca
  • Cristalografía de rayos X
  • Difracción del neutrón
  • Teoría dinámica de la difracción
• Estructura electrónica
  • Banda prohibida
  • Función de Bloch (Ondes d'electrón nun enrexáu (lattice))
  • Banda de conducción
  • Masa efeutivo
  • Buecu d'electrón
  • Gas de Fermi
    • Enerxía de Fermi
  • Líquidu de Fermi
  • Excitón
  • Banda de valencia
• Tresporte electrónicu
  • Oscilaciones de Bloch
  • Modelu de Drude
  • Conducción llétrica
  • Efeutu Hall
  • Magnetorresistencia
  • Superconductividá
• Carauterístiques mecániques
  • Modelu de Debye de calor específico
  • Elasticidá
  • Efeutu de Mössbauer
  • Fonón (vibraciones de redes cristalines)
  • Fraxilidá
• Carauterístiques óptiques
  • Óptica cristalina

Ver tamién

• Wikimedia Commons acueye conteníu multimedia sobre Física del estáu sólidu.
• Física de la materia entestada
• Metalografía
• Teoría de bandes

Referencies

Enllaces esternos

• Wikimedia Commons tien conteníu multimedia tocante a Física del estáu sólidu.
• fondu_24.html Entrevista al Dr. David Comedi investigador del llaboratoriu del sólidu (LAFISIO)de la Universidá Nacional de Tucumán(UNT)
• Online textbook: Introduction to Modern Solid State Physics by Yuri M. Galperin.

Plantía:Recordatoriu