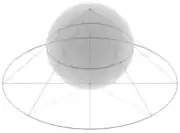
fig.1: Proyeición estereográfica del planu complexu estendíu sobre la "esfera de Riemann".
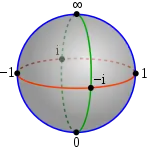	fig.2: La "esfera de Riemann" puede ser visualizada como'l planu complexu envueltu alredor d'una esfera.

En matemática, la esfera de Riemann (o planu complexu estendíu), llamada asina n'honor al matemáticu del sieglu XIX Bernhard Riemann, ye una esfera llograda del planu complexu por aciu la adición d'un puntu del infinitu. La esfera ye la representación xeométrica de los númberos complexos estendíos, denotado como ${\displaystyle {\hat {\mathbb {C} }}}$ ó ${\displaystyle \mathbb {C} \cup \{\infty \}}$,^[1] (vease fig.1 y fig.2), que consiste nos númberos complexos ordinarios en conxunción col símbolu ${\displaystyle \infty \!}$ pa representar el infinitu.

Los númberos complexos estendíos son comunes en analís complexu porque dexen la división per cero en delles circunstancies, nel sentíu de faer espresiones bien definíes tales como:

${\displaystyle 1/0=\infty }$

Por casu, cualesquier función racional sobre'l planu complexu pue ser estendida como una función continua sobre la esfera de Riemann, colos polos de la función racional mapeados al infinitu. Más xeneralmente, cualesquier función meromorfa pue ser pensada como una función continua que'l so codominio ye la esfera de Riemann.

En xeometría, la esfera de Riemann ye l'exemplu prototípicu d'una superficie de Riemann, y una de les más simples variedaes complexes. En xeometría proyectiva, la esfera puede ser pensada como la recta proyectiva complexa ${\displaystyle \mathbb {CP} ^{1}}$, l'espaciu proyectivo de toles rectes complexes en ${\displaystyle \mathbb {C} ^{2}}$. Como con cualquier superficie de Riemann compacta, la esfera tamién puede ser vista como una curva alxebraica proyectiva, faciendo d'esto un exemplu fundamental de xeometría alxebraica. Tamién atopa utilidá n'otres disciplines que dependen del analís y de la xeometría, como pue ser la mecánica cuántica y otres cañes de la física.

Ver tamién

• Álxebra de Witt
• Puntu del infinitu

Notes y referencies

• Brown, James and Churchill, Ruel (1989). Complex Variables and Applications. Nueva York: McGraw-Hill. ISBN 0070109052.
• Griffiths, Phillip and Harris, Joseph (1978). Principles of Algebraic Geometry. John Wiley & Sons. ISBN 0-471-32792-1.
• Penrose, Roger (2005). The Road to Reality. Nueva York: Knopf. ISBN 0-679-45443-8.
• Rudin, Walter (1987). Real and Complex Analysis. Nueva York: McGraw-Hill. ISBN 0071002766.
• Weisstein, Eric W. «Riemann sphere» (inglés). MathWorld. Wolfram Research.