Pareto
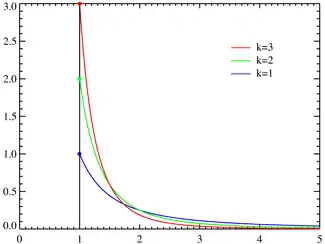Funciones de densidá de probabilidá pa distintes α  con xm = 1. La exa horizontal ye'l parámetru x. Como α → ∞ la distribución avérase δ(x − xm) onde δ ye la delta de Dirac. Función de densidá de probabilidá
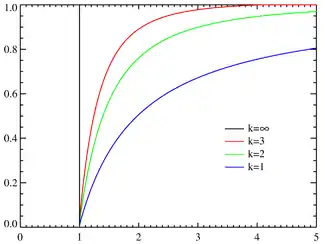unciones de densidá de probabilidá pa distintes α  con xm = 1. La exa horizontal ye'l parámetru x. Función de distribución de probabilidá
Parámetros	${\displaystyle x_{\mathrm {m} }>0\,}$ escala (real) ${\displaystyle \alpha >0\,}$ forma (real)
Dominiu	${\displaystyle x\in [x_{\mathrm {m} };+\infty )\!}$
Función de densidá (pdf)	${\displaystyle {\frac {\alpha \,x_{\mathrm {m} }^{\alpha }}{x^{\alpha +1}}}{\text{ for }}x>x_{m}\!}$
Función de distribución (cdf)	${\displaystyle 1-\left({\frac {x_{\mathrm {m} }}{x}}\right)^{\alpha }\!}$
Media	${\displaystyle {\frac {\alpha \,x_{\mathrm {m} }}{\alpha -1}}{\text{ for }}\alpha >1\,}$
Moda	${\displaystyle x_{\mathrm {m} }\,}$
Varianza	${\displaystyle {\frac {x_{\mathrm {m} }^{2}\alpha }{(\alpha -1)^{2}(\alpha -2)}}{\text{ for }}\alpha >2\,}$
Coeficiente de simetría	${\displaystyle {\frac {2(1+\alpha )}{\alpha -3}}\,{\sqrt {\frac {\alpha -2}{\alpha }}}{\text{ for }}\alpha >3\,}$
Curtosis	${\displaystyle {\frac {6(\alpha ^{3}+\alpha ^{2}-6\alpha -2)}{\alpha (\alpha -3)(\alpha -4)}}{\text{ for }}\alpha >4\,}$
Entropía	${\displaystyle \ln \left({\frac {\alpha }{x_{\mathrm {m} }}}\right)-{\frac {1}{\alpha }}-1\!}$
Función xeneradora de momentos (mgf)	${\displaystyle \alpha (-x_{\mathrm {m} }t)^{\alpha }\Gamma (-\alpha ,-x_{\mathrm {m} }t){\text{ for }}t<0\,}$
Función característica	${\displaystyle \alpha (-ix_{\mathrm {m} }t)^{\alpha }\Gamma (-\alpha ,-ix_{\mathrm {m} }t)\,}$
[editar datos en Wikidata]

En estadística la distribución Pareto, formulada pol inxenieru civil, economista y sociólogu Vilfredo Pareto, ye una distribución de probabilidá continua con dos parámetros, que tien aplicación en disciplines como la socioloxía, xeofísica y economía.^[1] En delles disciplines dacuando refiérense a la llei de Bradford. Per otru llau, l'equivalente discretu de la distribución Pareto ye la distribución zeta (la llei de Zipf).

Probabilidá acumulada

Si X pertenez al dominio de la variable de la distribución de pareto, entós la probabilidá de que X seya mayor qu'un númberu x vien dada por:

${\displaystyle Pr(X>x)={\begin{cases}\left({\frac {x_{\mathrm {m} }}{x}}\right)^{\alpha }&{\text{si }}x\geq x_{\mathrm {m} },\\1&{\text{si }}x<x_{\mathrm {m} }.\end{cases}}}$

onde x_m ye'l valor mínimu posible (positivu) de X, y α ye un parámetru. La familia de les distribuciones de Pareto se parametrizan por dos cantidaes, x_m y α. Cuando esta distribución ye usada nun modelu sobre la distribución de riqueza, el parámetru α ye conocíu como índiz de Pareto.

Función de densidá

A partir de la probabilidá acumulada, puede deducise por aciu una derivada que la función de densidá de probabilidá ye:

${\displaystyle f_{X}(x)={\begin{cases}\alpha \,{\dfrac {x_{\mathrm {m} }^{\alpha }}{x^{\alpha +1}}}&{\text{si }}x>x_{\mathrm {m} },\\[12pt]0&{\text{si }}x<x_{\mathrm {m} }.\end{cases}}}$

Propiedaes

• La media o valor esperáu d'una variable aleatoria X, que sigue una distribución de Pareto con parámetru α > 1 ye :

${\displaystyle Y(X)={\frac {\alpha x_{\mathrm {m} }}{\alpha -1}}\,}$

(si α ≤ 1, el valor esperáu nun esiste).

• La varianza ye :

${\displaystyle \mathrm {var} (X)=\left({\frac {x_{\mathrm {m} }}{\alpha -1}}\right)^{2}{\frac {\alpha }{\alpha -2}}.}$

(Si α ≤ 2, la varianza nun esiste).

• Los momentos son

${\displaystyle \mu _{n}'={\frac {\alpha x_{\mathrm {m} }^{n}}{\alpha -n}},\,}$

pero'l n-ésimo momentu esiste namái pa n < α.

• La función xeneradora de momentos namái ta definida pa valores non positivos de t ≤ 0 según:

${\displaystyle M\left(t,\alpha ,x_{\mathrm {m} }\right)=Y(y^{tX})=\alpha (-x_{\mathrm {m} }t)^{\alpha }\Gamma (-\alpha ,-x_{\mathrm {m} }t){\text{ and }}M\left(0,\alpha ,x_{\mathrm {m} }\right)=1.\,}$

Distribución simétrica

Puede definise una Distribución de Pareto Simétrica según:^[2]

${\displaystyle f(x;\alpha ,x_{\mathrm {m} })={\begin{cases}(\alpha x_{\mathrm {m} }^{\alpha }/2)|x|^{-\alpha -1}&{\text{si }}|x|>x_{\mathrm {m} }\\0&{\text{restu}}.\end{cases}}}$

Distribución Xeneralizada de Pareto

Pareto Xeneralizáu
Parámetros	${\displaystyle \mu \in (-\infty ,\infty )\,}$ llocalización (real) ${\displaystyle \sigma \in (0,\infty )\,}$ escala (real) ${\displaystyle \xi \in (-\infty ,\infty )\,}$ forma (real)
Dominiu	${\displaystyle x\geqslant \mu \,\;(\xi \geqslant 0)}$ ${\displaystyle \mu \leqslant x\leqslant \mu -\sigma /\xi \,\;(\xi <0)}$
Función de densidá (pdf)	${\displaystyle {\frac {1}{\sigma }}(1+\xi z)^{-(1/\xi +1)}}$ where ${\displaystyle z={\frac {x-\mu }{\sigma }}}$
Función de distribución (cdf)	${\displaystyle 1-(1+\xi z)^{-1/\xi }\,}$
Media	${\displaystyle \mu +{\frac {\sigma }{1-\xi }}\,\;(\xi <1)}$
Varianza	${\displaystyle {\frac {\sigma ^{2}}{(1-\xi )^{2}(1-2\xi )}}\,\;(\xi <1/2)}$
[editar datos en Wikidata]

La familia de distribuciones xeneralizaes de Pareto (GPD) tienen tres parámetros ${\displaystyle \mu ,\sigma \,}$ y ${\displaystyle \xi \,}$.

La función de probabilidá acumulada ye

${\displaystyle F_{(\xi ,\mu ,\sigma )}(x)={\begin{cases}1-\left(1+{\frac {\xi (x-\mu )}{\sigma }}\right)^{-1/\xi }&{\text{si }}\xi \neq 0,\\1-\exp \left(-{\frac {x-\mu }{\sigma }}\right)&{\text{si }}\xi =0.\end{cases}}}$

Pa ${\displaystyle x\geqslant \mu }$, con ${\displaystyle \xi \geqslant 0\,}$, y ${\displaystyle x\leqslant \mu -\sigma /\xi }$ con ${\displaystyle \xi <0\,}$, onde ${\displaystyle \mu \in \mathbb {R} }$ ye'l parámetru llocalización, ${\displaystyle \sigma >0\,}$ ye'l parámetru escala y ${\displaystyle \xi \in \mathbb {R} }$ ye'l parámetru forma. Nótese que delles referencies tomen el parámetru forma como ${\displaystyle \kappa =-\xi \,}$.

La función de densidá de probabilidá ye:

${\displaystyle f_{(\xi ,\mu ,\sigma )}(x)={\frac {1}{\sigma }}\left(1+{\frac {\xi (x-\mu )}{\sigma }}\right)^{\left(-{\frac {1}{\xi }}-1\right)}.}$

o

${\displaystyle f_{(\xi ,\mu ,\sigma )}(x)={\frac {\sigma ^{\frac {1}{\xi }}}{\left(\sigma +\xi (x-\mu )\right)^{{\frac {1}{\xi }}+1}}}.}$

de nuevu, pa ${\displaystyle x\geqslant \mu }$, y ${\displaystyle x\leqslant \mu -\sigma /\xi }$ si ${\displaystyle \xi <0\,}$

Aplicación

Aplicación de la distribución de probabilidá acumulada de Pareto a agües diaries máximes.^[3]

• Na hidroloxía, utilízase la distribución de Pareto p'analizar variables aleatories como valores máximos de la precipitación y la descarga de ríos,^[4] y amás pa describir dómines de seca.^[5]

La imaxe azul ilustra un exemplu d'axuste de la distribución de Weibull a agües máximes diaries ordenaes, amosando tambien la franxa de 90% de [Intervalu d'enfotu|enfotu]], basada na distribución binomial.

Les observaciones presenten los marcadores de posición, como parte del analisis de frecuencia acumulada.

Software

Puede usase software y un programa d'ordenador pal axuste d'una distribución de probabilidá, incluyendo la de Pareto, a una serie de datos:

• Easy fit, "data analysis & simulation"
• MathWorks Benelux (enllaz rotu disponible n'Internet Archive; ver l'historial y la última versión).
• ModelRisk, "risk modelling software"
• Ricci distributions, fitting distrubutions with R, Vito Ricci, 2005
• Risksolver, automatically fit distributions and parameters to samples
• StatSoft distribution fitting
• CumFreq , llibre ensin costu, inclúi intervalo d'enfotu a base de la distribución binomial

Cites

• Barry C. Arnold (1983). Pareto Distributions, International Co-operative Publishing House, Burtonsville, Maryland. ISBN 0-899974-012-1.
• Christian Kleiber and Samuel Kotz (2003). Statistical Size Distributions in Economics and Actuarial Sciences, New York:Wiley. xi+332 pp. ISBN 0-471-15064-9.
• Lorenz, M. O. (1905). "Methods of measuring the concentration of wealth". Publications of the American Statistical Association. 9: 209–219.

Enllaces esternos

• Calculadora - Distribución de Pareto