| Coordenaes cartesianes | |
|---|---|
|
sistema de coordenadas ortogonales (es) | |
 | |

Les coordenaes cartesianes o coordenaes rectangulares (sistema cartesianu) son un tipu de coordenaes ortogonales usaes n'espacios euclídeos, pa la representación Gráfica d'una función gráfica d'una rellación matemática (funciones matemátiques y ecuaciones de xeometría analítica), o del movimientu o posición en física, caracterizaes por tener como referencia exes ortogonales ente sigo qu'alleguen nel puntu orixe. Nes coordenaes cartesianes determinar les coordenaes al orixe como'l llargor de caúna de les proyeiciones ortogonales d'un puntu dau sobre cada unu de les exes. La denominación de 'cartesianu' introducir n'honor de René Descartes, quien les utilizó per primer vegada de manera formal.
El sistema en sí ye un sistema bidimensional, que se denomina planu cartesianu. El puntu d'intersección de les rectes, por definición, considera como'l puntu cero de les rectes y conozse como orixe de coordenaes. A la exa horizontal o de les ascises asígnase-y los númberos reales de les xes ("x"); y a la exa vertical o de les ordenaes asígnense-y los númberos reales de les yes ("y"). Al cortase los dos rectes, estremen al planu en cuatro rexones o zones, que se conocen col nome de cuadrantes:
- Primer cuadrante "I": Rexón cimera derecha *Segundu cuadrante "II":
Rexón cimera izquierda *Tercer cuadrante "III": Rexón inferior izquierda *Cuartu cuadrante "IV": Rexón inferior derecha El planu cartesianu utilizar p'asigna-y un allugamientu a cualquier puntu nel planu. Na gráfica indica'l puntu +2 nes ascises y +3 nes ordenaes. El conxuntu (2 , 3) denominar "par ordenáu" y de la mesma pueden allugase otros puntos.
Les coordenaes cartesianes úsense por casu pa definir un sistema cartesianu o sistema de referencia respectu yá seya a una sola exa (llinia recta), al respective de dos exes (un planu) o al respective de tres eje (nel espaciu), perpendiculares ente sigo (planu y espaciu), que se corten nun puntu llamáu orixe de coordenaes. Nel planu, les coordenaes cartesianes denominar ascisa y ordenada. L'ascisa ye la coordenada horizontal y represéntase davezu pola lletra x, ente que la ordenada ye la coordenada vertical y represéntase pola y.
Historia

Denominar coordenaes cartesianes n'honor a René Descartes (1596-1650), el célebre filósofu y matemáticu francés que quixo encontar el so pensamientu filosóficu nel métodu de tomar un puntu de partida evidente sobre'l qu'edificaría tou la conocencia.
Como creador de la xeometría analítica, Descartes tamién empezó tomando un puntu de partida» nesta disciplina, el sistema de referencia cartesianu, pa poder representar la xeometría plana, qu'usa namái dos rectes perpendiculares ente sigo que se corten nun puntu denomináu «orixe de coordenaes».
Planu cartesianu
Con un sistema de referencia conformáu por dos rectes perpendiculares que se corten nel orixe , cada puntu del planu puede "nomase" por aciu dos númberos: (x, y), que son les coordenaes del puntu, llamaes ascisa y ordenada, respeutivamente, que son les distancies ortogonales de dichu puntu al respective de les exes cartesianes.
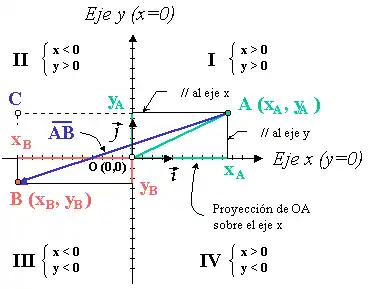
La ecuación de la exa ye , y la de la exa ye , rectes que se corten nel orixe , que les sos coordenaes son .
Denominar tamién exa de les ascises a la exa , y exa de les ordenaes a la exa . Les exes estremen l'espaciu en cuatro cuadrantes I, II, III y IV, nos que los signos de les coordenaes alternen de positivu a negativu (por casu, los dos coordenaes del puntu A van ser positives, ente que les del puntu B van ser dambes negatives).
Les coordenaes d'un puntu cualesquier van venir daes poles proyeiciones del segmentu ente l'orixe y el puntu sobre cada unu de les exes.
Sobre cada unu de les exes defínense vectores unitarios (i y j) como aquellos paralelos a les exes y de módulu (llargor) la unidá. En forma vectorial, la posición del puntu A defínese respectu del orixe coles componentes del vector OA.
La posición del puntu A va ser:
Nótese que la llista de coordenaes puede espresar tantu la posición d'un puntu como les componentes d'un vector en notación matricial.
La distancia ente dos puntos cualesquier va venir dada pola espresión:
Aplicación del teorema de Pitágoras al triángulu rectángulu ABC.
Un vector cualesquier AB va definise restando, coordenada a coordenada, les del puntu d'orixe de les del puntu de destín:
Evidentemente, el módulu del vector AB va ser la distancia dAB ente los puntos A y B antes calculada.
Espaciu euclideu
Si tenemos un sistema de referencia formáu por trés rectes perpendiculares ente sigo (X, Y, Z), que se corten nel orixe (0, 0, 0), cada puntu del espaciu puede nomase por aciu tres números: (x, y, z), denominaos coordenaes del puntu, que son les distancies ortogonales a los trés planos principales: los que contienen les pareyes d'exes YZ, XZ y YX, respeutivamente.

Los planos de referencia XY (z = 0); XZ (y = 0); y YZ (x = 0) estremen l'espaciu n'ocho cuadrantes nos que, como nel casu anterior, los signos de les coordenaes pueden ser positivos o negativos.
La xeneralización de les rellaciones anteriores al casu espacial ye inmediata considerando qu'agora ye necesaria una tercera coordenada (z) pa definir la posición del puntu.
Les coordenaes del puntu A van ser:
y el B:
La distancia ente los puntos A y B va ser:
- .
El segmentu AB va ser:
Cambéu del sistema de coordenaes
Tantu nel casu planu como nel casu espacial pueden considerase tres transformación elementales: traslación del orixe, rotación alredor d'una exa y esguiláu.
Traslación del orixe

Suponiendo un sistema de coordenaes inicial S1 con orixe en O y exes x y y
y les coordenaes d'un puntu A dadu, sían nel sistema S1:
dau un segundu sistema de referencia S2
Siendo los centros de coordenaes de los sistemes 0 y 0´, puntos distintos, y les exes x, x´; y y, y´ paralelos dos a dos, y les coordenaes de O´, al respective de S1:
Dizse traslación del orixe, a calcular les coordenaes de A en S2, según los datos anteriores, que vamos llamar:
Daos los puntos O, O´ y A, tenemos la suma de vectores:
estenando :
Lo que ye lo mesmo que:
Dixebrando los vectores por coordenaes:
y ampliándolo a tres dimensiones:
Rotación alredor del orixe

Dau un sistema de coordenaes nel planu S1 con orixe en O y exes x y y:
y una base ortonormal d'esti sistema:
Un puntu A del planu va representar nesti sistema según les sos coordenaes:
Pa un segundu sistema S2 de referencia xiráu un ángulu , respectu al primeru:
y con una base ortonormal:
Al cálculu de les coordenaes del puntu A, al respective de esti segundu sistema de referencia, xiráu respectu al primeru, llámase rotación alredor del orixe, siendo la so representación:
Hai que tener en cuenta que'l puntu y son el mesmu puntu, ; emplégase una denominación o otra pa indicar el sistema de referencia emplegáu. El valor de les coordenaes al respective de unu o otru sistema, sí son distintos, y ye lo que pretende calculase.
La representación de B1 en B2 ye:
Puesto que el puntu A en B1 ye:
col tresformamientu anterior tenemos:
Y, desfaciendo los paréntesis:
reordenando:
Como:
- ;
Tenemos que:
Como sabíamos:
Por identificación de términos:
Que son les coordenaes de A en B2, en función de les coordenaes de A en B1 y de .
Esguiláu
Sía un puntu con coordenaes (x,y) nel planu. Si camuda la escala de dambes exes nun factor λ, les coordenaes de dichu puntu nel nuevu sistema de coordenaes van pasar a ser:
El factor d'escala λ non necesariamente tien de ser el mesmu pa dambes exes.
Cálculu matricial
Siendo [T] la matriz de tresformamientu y que les sos files son igualmente les componentes de los vectores unitarios i ' y j ' respectu de los orixinales i y j, o si prefierse, que les sos columnes son les componentes de los vectores unitarios orixinales nel sistema de referencia rotado.
.png.webp)
Nota: Les magnitúes vectoriales tán en negrina.
Ver tamién
- Cuadrante (xeometría)
- Anamorfosis
- Base
- Base canónica
- Base ortogonal
- Base ortonormal
- Coordenaes polares
- Combinación llinial
- Espaciu vectorial
- Xeodésica
- Independencia llinial
- Productu angular
- Productu mistu
- Productu tensorial
- Productu vectorial
- Sistema xenerador
- Topoloxía
Referencies
- «Cartesian Coordinate System» (inglés). Cut the knot.
- Weisstein, Eric W. «Sistema de coordenaes» (inglés). MathWorld. Wolfram Research.
- Weisstein, Eric W. «Coordenaes cartesianes» (inglés). MathWorld. Wolfram Research.
Referencies
Enllaces esternos
- Coordenaes cartesianes, esplicación interactiva (riqui java)
- Proyeutu didácticu pa introducción al planu cartesianu en llinguaxe de programación Logo.