Bisectriz
Bisección (es) Traducir
llugar xeométricu y Semirreuta
Cambiar los datos en Wikidata

La bisectriz d'un ángulu ye la reuta que dixebra l'ángulu en dos partes iguales.

Propiedá

Tolos puntos allugaos na bisectriz son equidistantes a los dos llaos (reutes) del ángulu.

Recíprocamente, dos reutes, al cruciase, determinen cuatro ángulos cóncavos. Caún d'ellos define una bisectriz. Estes bisectrices resulten ser el llugar xeométricu de los puntos equidistantes de les dos reutes. Esti resultáu afítase cenciellamente, namái adicando que cada bisectriz, ye l'exe de simetría del so ángulu: la simetría axal respeutu d'una bisectriz dexa el ángulu invariable.

Na figura de la izquierda, la bisectriz interior al ángulu xOy (en mariellu) ye (zz'), y l'esterior ye (ww'). Córtense formando un ángulu reutu. N'efeutu, si nomamos a la midida de xOz, y b la de yOw, decatámonos que 2a + 2b ye la midida del ángulu xOx' , que ye planu. Dixebrando por 2: zOw mide a + b = 90º.

Aplicación

Les tres bisectrices de los ángulos internos d'un triángulu, córtense nún puntu únicu, qu'equidista de los llaos. Esti puntu nómase l'incentru del triángulu, y ye'l centru de la circunferencia inscrita al triángulu. Esta circunferencia, ye tanxente a caún de los llaos del triángulu.

Demostración

Dos bisectrices del triángulu nun pueden ser paraleles. Seya O la interseición de les bisectrices D y D' (ver figura). Como O pertenez a D, ye equidistante de les reutes (AB) y (AC). Como O pertenez a D' , entós tamién equidista de les reutes (AB) y (BC). Por transitividá de l'igualdad, ye equidistante de (AC) y (BC), y pertenez a la bisectriz (interior) del ángulu C, ye dicir a D" . Al ser equidistante a los tres llaos. Poro, la circunferencia que'l so radiu seya xustamente la distancia común del puntu O a los llaos del triángulu, ye tanxente a caún de los llaos.

Otres propiedaes

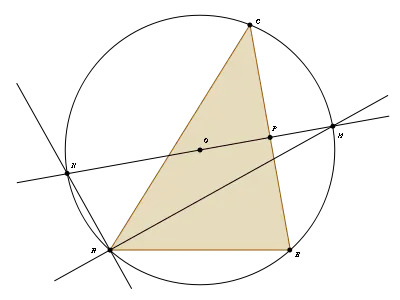
Seya'l triángulu ABC y la circunferencia circunscrita. La mediatriz MN, del llau BC, corta l'arcu BMC nel so puntu mediu. Como l'ángulu inscritu BAC subtiende talu arcu, los ángulos BAM y MAC son iguales y la reuta AM ye la bisectriz del ángulu BAC. Les reutes AN y AM son ortogonales, porque'l llau MN del triángulu AMN ye diámetru de la circunferencia, y el vértiz A afáyase so la circunferencia. La reuta AN y bisectriz del ángulu esterior al triángulu del vértiz A.

Esto quier dicir, que: «La mediatriz d'un llau d'un triángulu y les bisectrices del ángulu aviesu interséutense so la circunferecia circunscrita».


Referencies

    Enllaces esternos

    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.