نماذج جزيئية
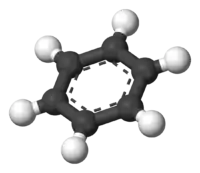
مقدمة
استند الكيميائيون على مبدأي البساطة والقوة التفسيرية لأشكال النماذج الجزيئية للمركبات الكيميائية في وقت مبكر من عام 800 , وبمرور الزمن كان من الطبيعي تطوير النظريات والرياضيات للمساعدة في فهم التركيب الجزيئي وفهم تغيرات الأشكال مع التفاعلات الكيميائية. فبهذا التطوير توسع مصطلح الأشكال الجزيئية - على مدى العقود الماضية - من أداة لتصور الأشكال ثلاثية الأبعاد وتحليل خصائص الجزيئات وسلوكها على المستوى الذري، إلى استخراج قاعدة بيانات وإجراء فحص الأدوية بالتمثيل ثلاثي الأبعاد للمركب.
وتُستَخدم كل الطرق، النظرية والحسابية، لنمذجة وتمثيل سلوك الجزيئات، ومن هذه الطرق تلك المستخدمة في مجالات الكيمياء الحسابية، وتصميم الدواء، وعلم الأحياء الحسابي وعلوم المواد، إذ توظف جميعها لدراسة الأنظمة الجزيئية الممتدة من أنظمة الكيمياء الصغيرة إلى كبيرة الجزيئات، وحتى إلى المركبات البيولوجية الكبيرة.
أبسط الحسابات يمكن أن تؤدى يدويا، لكن لابد من وجود أجهزة الكمبيوتر اللازمة لأداء النماذج الجزيئية لأي نظام معقول الحجم. السمة المشتركة لتمثيل اشكال النماذج الجزيئية هي وصف المستوى الذري للأنظمة الجزيئية.
يمكن أن يشمل ذلك معالجة الذرات كأصغر وحدة فردية (نهج الميكانيكيا الجزيئية), أو وضع نماذج إلكترونات صريحة ومستقلة لكل ذرة (نهج الكيمياء الكمية).
الآليات الجزيئية
الآليات الجزئية هي أحد جوانب النماذج الجزيئية، كما أنها تشير إلى استخدام الميكانيكا الكلاسيكية (الآلية النيوتنية) لوصف الأساس المادي وراء النماذج. وعادة ما تصف النماذج الجزيئية الذرات (النواة والإلكترونات بشكل جماعي كرسم نقطة مرتبطة بالكتلة. إذ يتم وصف التفاعل بين الذرات من خلال روابط كيميائية وتكون كالنابض. وتفاعلات كيميائية تنشأ نتيجة القوة الكهرومغناطيسية، ويتم حسابها بناء على قانون كولوم حيث ترتبط الإلكترونات (سالبة الشحنة) مع نواة الذرة (موجبة الشحنة)، فتنشأ الروابط بين الذرات. كما وتستخدم قاعدة لينارد جونز لوصف التفاعلات الكهربائية بين الذرات والجزيئات المتعادلة الشحنات. إذ يتم تعيين الإحداثيات لسرعة تفاعل الذرات في الفضاء الديكارتي أو في الإحداثيات الداخلية، وترتبط هذه السرعة بالمحاكاة الديناميكية والسرعة الجزيئية، وهي كمية ماكروسكوبية. ويطلق على التعبير الرياضي المعتمد في قياسها (الوظيفة الكامنة) ويرتبط بالطاقة الداخلية للنظام.
إن كمية الديناميكية الحرارية تساوي مجموع الطاقات الكامنة والحركية. وطرق تقليل الطاقة لتقليل الطاقة الكامنة (طاقة الوضع) متعددة، منها: طريقة الهبوط الأكثر انحدارا باستخدام طريقة لابلاس، وطريقة التدرج المتقارن التي تعتمد على نسبة الانحدار باستخدام اللوغاريتم، في حين أن الطرق التي تصور سلوك النظام مع امتداد الوقت يطلق عليها الديناميكيات الجزيئية.
وتحسب الوظيفة الكامنة من الطاقة الكامنة الجزيئية وهي مجموع الطاقات التي تصف الانحراف من أطوال وزوايا الروابط وزوايا الالتواء بعيدا عن قيم التوازن، بالإضافة للذرات غير المرتبطة ممثلة بروابط «بفان دير والز» والروابط الكهروستاتيكية، وكل هذه العوامل يطلق عليها مجال القوة.
مجموعة المتغيرات تحتوي على أطوال الروابط المتوازنة وزوايا الروابط وقيم الشحنة الجزئية وثوابت القوة ومتغيرات «فان دير فال» ز جميعها يطلق عليها مجال القوة.
وهناك تطبيقات مختلفة من الميكانيكا الجزيئية تستخدم تعبيرات رياضية مختلفة ومتغيرات مختلفة للوظيفة الكامنة.وقد تم تطوير حقول القوة المشتركة المستخدمة اليوم باستخدام حسابات الكم عالية المستوى و/ أو المناسبة للبيانات التجريبية. وتستخدم هذه الطريقة، التي يطلق عليها «تقليل الطاقة»، للعثور على مواضع الميل «ذات الصفر» لجميع الذرات، وبعبارة أخرى، الحد الأدنى للطاقة المحلية. وتعد الحالات منخفضة الطاقة الأكثر استقرارا، ويتم البحث فيها عادة بسبب دورها في العمليات الكيميائية والبيولوجية. ومن ناحية أخرى، يمكن القول بأن محاكاة الديناميكيات الجزيئية تحسب سلوك النظام بدالة للوقت. وهو ينطوي على حل قوانين نيوتن للحركة، وعلى رأسها القانون الثاني (F=ma) . وبدمج قوانين نيوتن للحركة، وذلك باستخدام خوارزميات التكامل المختلفة، فإن هذا يؤدي إلى مسارات ذرية في الفراغ والزمن.
وتعرف القوة نسبة إلى الذرة بأنها (الميل السلبي لوظيفة الطاقة المحتملة). وطريقة الحد من الطاقة مفيدة للحصول على صورة ثابتة للمقارنة بين حالات المادة من أنظمة مماثلة، في حين الديناميكيات الجزيئية توفر معلومات عن العمليات الديناميكية مع الإدراج الفعلي لآثار درجة الحرارة.
أنواع الرسم البياني للنماذج الجزيئية
نموذج ملء الفراغ (Space-filling model)
وهو نموذج ثلاثي الأبعاد يستخدم في الكيمياء، حيث تمثل كل كرة أحد ذرات المركب، بحيث تتناسب أقطار الكرات مع أقطار الذرات، وكذلك تتناسب المسافة بين مراكز الكرات مع المسافة بين أنوية الذرات بنفس مقياس الرسم، ويتم تمثيل العناصرالمختلفة بكرات ذات ألوان مختلفة. ويعد هذا النموذج مهما لرؤية الشكل والأبعاد النسبية للجزيء.
نموذج الكرة والعصا (Ball & stick)
و تتمثل فيه الجزيئات بشكل كرة وعصا، إذ تمثل الكرة الذرات وتمثل العصا الروابط بين تلك الذرات، ويمكن لهذا النموذج أن يظهر مجموعة واسعة من الخصائص، مثل الشكل، والحجم النسبي، والمرونة، وهناك العديد من الأشكال للنماذج الجزيئية ومنها – وهو الأكثر شهرة - نموذج «واتسون كريك» للحمض النووي (د ن إي).
نموذج الإطارالسلكي (wire frame model)
و تتمثل فيه الجزيئات بوساطة ربط القمم المكونة للجزيء باستخدام خطوط مستقيمة، وذلك باستخدام رسومات الحاسوب، وعرضه كجسم ثلاثي الأبعاد.
نموذج العصي (Sticks)
يكون برسم العصا لتمثيل الروابط التي تصل بين الذرات.
المتغيرات
يمكن نمذجة الجزيئات إما في فراغ، أو في وجود مذيب مثل الماء. ويشار إلى محاكاة النظم في الفراغ على أنها محاكاة طور الغاز، في حين أن تلك التي تتضمن وجود جزيئات المذيبات يشار إليها على أنها محاكاة المذيبات الصريحة. في نوع آخر من المحاكاة، ويقدّر تأثير المذيبات باستخدام تعبير رياضي تجريبي، وتسمى هذه بظاهرة الإذابة الضمنية.
تنسيق التمثيل
تعتمد معظم حقول القوة على المسافة، مما يجعل التعبيربالإحداثيات الديكارتية هي الأكثر ملائمة للاستخدام، ومع ذلك فإن الطبيعة الجامدة للروابط التي تحدث بين ذرات معينة تحدد ما هو جوهر تصاميم الجزيئات التي جعلت نظام الإحداثيات الداخلية الأكثر منطقية للتمثيل. في بعض المجالات التمثيل الذي يدعى IC (طول الرابطة، وزاوية تطور الرابطة) ويسمى تمثيل Z أو تمثيل التواء الزاوية.
ولسوء الحظ تتطلب الحركات المستمرة في الفراغ الديكارتي في كثير من الأحيان إلى فروع متقطعة للزاويا في الإحداثيات الداخلية مما يجعل العمل مع حقول القوة صعب نسبيا في التمثيل الإحداثي الداخلي وعلى العكس من ذلك فإن النزوح البسيط للذرة في الفراغ الديكارتي قد لا يكون على المسار المستقيم، وذلك بسبب المنع من الروابط المترابطة، وعليه، تستخدم برامج حسابية لتحديد الاستخدام الأمثل لقلب ورفع ما بين التمثيلات خلال تكرارهم.
و يمكن أن يسيطر على حساب الإمكانات نفسها وفي جزيئات السلسلة الطويلة مما يقود إلى أخطاء تراكمية عدديا. بينما كل التحويلات اللوغاريتمية تنتج حسابيا نتائج متطابقة، وبالتالي فالطريقتين تختلف من حيث السرعة والدقة العددية، ان أسرع وأدق التواء للتحويل الديكارتي حاليا هو طريقة الإطار المرجعي الإرشادي الطبيعي (NeRF)[1]
التطبيقات
تستخدم طريقة النمذجة الجزيئية حاليا بشكل روتيني لفحص التراكيب الكيميائية، ودراسة الديناميكية لها، ودراسة خصائص سطحها، ودراسة أنظمة البوليمر.كما أنها تستخدم لفحص أنواع الأنشطة البيولوجية التي تشمل: التفاف البروتين، والتغيرات التوافقية المرتبطة بوظيفة الجزيئية البيولوجية والتقدير الجزيئي للبروتينات، الحمض النووي، والأغشية المعقدة وكذلك تستخدم لتطوير الدواء.
مراجع
- Parsons, J., Holmes, J. B., Rojas, J. M., Tsai, J., Strauss, C. E., Practical conversion from torsion space to cartesian space for in silico protein synthesis. [1] J Comput Chem 26 (2005), 1063-1068.[2]
- بوابة الفيزياء
- بوابة الكيمياء