نسبة تبادلية

تُعمم النسبة التبادلية لتشمل الدائرة بتعريف المستوى العقدي بالصيغة الآتية: ${\displaystyle (z_{1},z_{2};z_{3},z_{4})={\frac {(z_{3}-z_{1})(z_{4}-z_{2})}{(z_{3}-z_{2})(z_{4}-z_{1})}}.}$. إذا كانت النقاط ${\displaystyle A,C,B}$ مُتسامتةً في المستوى العقدي كما الشكل، فإنَّ دائرة أبولونيوس لهذه الثلاث نقاط هي مجموعة النقاط ${\displaystyle P}$ التي تحقق أن معيار النسبة التبادلية مساوية لواحد.${\displaystyle |[A,B;C,P]|=1.\ }$. بمعنىً آخر: ${\displaystyle P}$ هي نقطة على دائرة أبولونيوس للنقاط ${\displaystyle A,C,B}$ إذا وفقط إذا كان معيار النسبة التبادلية ${\displaystyle [A,B;C,P]}$ مساوياً للواحد.[5][6][7]

تعريف أبولونيوس للدائرة.

تُعرّفُ النقطة ${\displaystyle D}$ على أنّها المرافق التوافقي للنقطة ${\displaystyle C}$ بالنسبة لـ${\displaystyle A}$ و${\displaystyle B}$. إذا كانت النسبة التوافقية للنقاط الأربع تساوي ${\displaystyle -1}$. وتُسمَّى حينئذٍ نسبةً توافقية. ونتيجةً لذلك، فإنَّ النسبة التبادلية بالإمكان اعتبارها على أنها مدى بُعدِ الأربع نقاط عن النسبة التوافقية.[4] النسبة التبادلية مُعرّفة منذ القِدَم، حيث يرجّح أن إقليدس هو أوّل من ذكرها، كما استعملها ببس الرومي الذي لاحظ خاصيّة ثباتها تحت التحويلات الخطية. فالنسبة التبادلية لأيِّ قطعةٍ مُستقيمةٍ تقطع 4 مستقيمات متلاقية هي ثابتة. بشكلٍ مُكافئ، يُعرّفُ ذلكَ في الهندسة الإسقاطية على أنَّ النسبة التبادلية ثابتةٌ تحت أي تحويلٍ خطيٍ كسريٍ.[4] في تعريفِ أبولونيوس للدائرة، تُسمَّى الخطوط ${\displaystyle {\overleftrightarrow {PA}},{\overleftrightarrow {PB}},{\overleftrightarrow {PC}},{\overleftrightarrow {PD}}}$ «حُزمة توافقية» وهي كل مجموعة خطوط متلاقية نسبتها توافقية (أي: نسبتها التبادلية تساوي ${\displaystyle -1}$). إنَّ تقاطعَ حُزمةٍ توافقيةٍ مع الدائرة يُنتجُ رباعياً توافقياً.[8]

• 
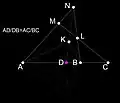  النسبة التناغمية في الهندسة الإسقاطية ، هي النسبة الموجودة بين أربع نقاط متسامتة (A,B,C,D)، التي علاقتها التبادلية تسمى رباعية تناغمية. يمكن إنشاء هذه الرباعية بدءًا من رباعي أضلاع M,N,L,K

• مبرهنة منصف الزاوية.
• دوائر أبولونية.
• دائرة.
• رباعي تناغمي.

• بوابة رياضيات
• بوابة هندسة رياضية