منحنى بيزيه
منحنى بيزيه أو منحنى بيزير هو منحنى وسيطي يستخدم بشكل شائع في الرسوميات الحاسوبية والحقول العلمية المتعلقة.[1][2][3] عند رفع درجة منحنى بيزير إلى الدرجات الأعلى ينتج ما يعرف باسم سطح بيزييه.
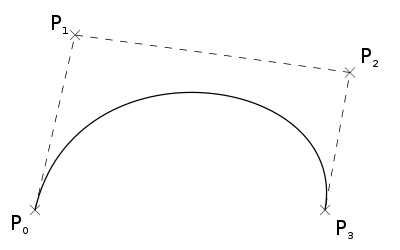
في الرسوميات الحاسوبية يتم استخدام منحنى بيزيه من أجل وصف الخطوط (مثل: بوست سكريبت وأوبن تايب), وكذلك من أجل عمل المنحنيات والسطوح في CAD, وكذلك في الرسوميات المتجهية(مثل: رسوميات متجهية متغيرة تصميم بمساعدة الحاسوب).
تم تطوير منحنيات بيزيه على يد المهندس الفرنسي بيير بيزييه عام 1962 والذي استخدمها لتصميم أجسام السيارات، وقد تم وصف المنحنيات لأول مرة عام 1959 على يد باول دوكاستلجو في أعماله المتعلقة بخوارزمية دوكاستلجو.
تطبيقات
الرسوم الحاسوبية
تستخدم منحنيات بيزيه بشكل واسع في الرسومات الحاسوبية من أجل رسم منحنيات ناعمة وسلسة. المنحنى يقع بشكل كلي داخل الإنغلاق المحدب للنقاط، لذلك يتم استخدام هذه النقاط بكل سهولة لتشكيل المنحنى المطلوب.
يمكن تطبيق التحويل التآلفي (مثل الدوران والإنزلاق) على المنحنى من خلال تطبيق هذا التحويل على نقاط التحكم لهذا المنحنى.
الرسوم المتحركة (تحريك)
في تطبيقات الرسوم المتحركة مثل ادوب فلاش أدوبي فلاش و Synfig [الإنجليزية] يتم استخدام منحنيات بيزيه في الرسم مثل رسم الصور المتحركة. حيث يقوم المستخدم برسم المسار باستخدام منحنى بيزيه, ويتولى التطبيق مهمة التحضير لحركة هذا العنصر على طول المسار المرسوم مسبقاً. وكذلك في الرسوم الثلاثية الأبعاد يتولى منحنى بيزيه رسم المسارات ثلاثية الأبعاد.
رسم الحروف
يستعمل منحنى بيزيه في رسم الحروف على جهاز الحاسوب، وكذلك أنظمة التصوير الحديثة مثل بوست سكريبت وSVG تستخدم منحنيات بيزيه من أجل رسم الأشكال المنحنية.
معادلة منحنى بيزيه
من الممكن وصف منحنى بيزيه من الدرجة n على الشكل التالي. من أجل مجموعة نقاط P0, P1,..., Pn، فإن منحنى بيزيه يعطى بالعلاقة :
حيث أن e هو المعامل الثنائي.
مثال
من أجل n = 5 يكون منحنى بيزيه بالشكل :
طريقة رسم منحنى بيزيه
منحنى خطي
![Animation of a linear Bézier curve, t in [0,1]](../I/B%C3%A9zier_1_big.gif) |
| رسم لتوضيح منحنى بيزيه من الدرجة الثانية, t تقع في الفترة [0,1] |
تستخدم t في اقتران المنحنى الخطي للتعبير عن بعد (B(t على الخط الواقع بين النقطتين P0 وP1.
فمثلاً عندما تكون t=0.25 فان (B(t تكون هي الربع الأول من المسافة الواصلة بين P0 و P1. في الرسمة الجانبية تتغير t بين القيمتين 0 و 1, بينما تصف (B(t الخط المستقيم الواقع بين P0 و P1.
منحنى من الدرجة الثانية
في منحنى بيزيه من الدرجة الثانية نستطيع ان ننشئ نقاط متوسطة مثل Q0 و Q1. وهذه النقاط تحمل قيمة تقع في الفترة [1,0]:
- النقطة الأولى (Q0(t تقع بين P0 و P1 وتصف منحنى بيزيه الخطي بين هاتين النقطتين.
- النقطة الثانية (Q1(t تقع بين P1 و P2 وتصف منحنى بيزيه الخطي على هاتين النقطتين.
- النقطة (B(t تقع على الخط الواصل بين النقطتين (Q0(t و (Q1(t وتصف منحنى بيزيه من الدرجة الثانية.
انظر للرسمة الجانبية التي توضح ذلك. لاحظ اننا رسمنا خط افتراضي بين (Q0(t و (Q1(t ووضعنا (B(t عليه، وبالتالي تكون النقطة B هي نتيجة الرسم ومن ثم نصل نقطة البداية مع B ثم مع نقطة النهاية فينتج لدينا المنحنى المطلوب.
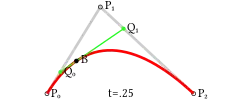 | ![Animation of a quadratic Bézier curve, t in [0,1]](../I/B%C3%A9zier_2_big.gif) | |
| إنشاء منحنى بيزيه من الدرجة الثانية | رسم متحرك لمنحنى بيزيه من الدرجة الثانية، حيث أن t تقع في الفترة [0,1] |
منحنى بيزيه من الدرجة الثالثة
في منحنى بيزيه كلما زادت الدرجة كلما زاد عدد النقاط المتوسطة التي نحتاجها. ففي المنحنى من الدرجة الثالثة نحتاج إلى ثلاث نقاط متوسطة Q0 و Q1 و Q2, والتي تصف منحنى بيزيه الخطي لهذا الشكل، وكذلك نحتاج إلى نقطتي R0 و R1 لتصف منحنى بيزيه من الدرجة الثانية لهذا الشكل وفي الاخير نضع (B(t على الخط الواصل بين R0 و R1.
 | ![Animation of a cubic Bézier curve, t in [0,1]](../I/B%C3%A9zier_3_big.gif) | |
| إنشاء منحنى بيزيه من الدرجة الثالثة | رسم لإنشاء منحنى بيزيه من الدرجة الثالثة، حيث أن t تقع في [0,1] |
منحنى بيزيه من الدرجة الرابعة
نحتاج إلى النقاط التالية:
- 4 نقاط لتصف المنحنى الخطي.
- 3 نقاط لتصف المنحنى من الدرجة الثانية.
- نقطتين لتصف المنحنى من الدرجة الثالثة.
- النقطة (B(t والتي تقع على S0 و S1 ومن ثم نرسم المنحنى.
 | ![Animation of a quartic Bézier curve, t in [0,1]](../I/B%C3%A9zier_4_big.gif) | |
| إنشاء منحنى بيزيه من الدرجة الرابعة | رسم منحنى بيزيه من الدرجة الرابعة، حيث أن t تقع في الفترة [0,1]. |
منحنى بيزيه من الدرجة الخامسة
يتم إنتاجه بطريقة مشابهة للمنحنيات السابقة.
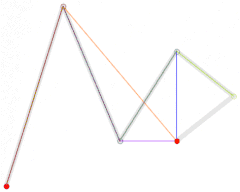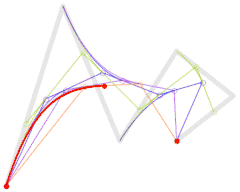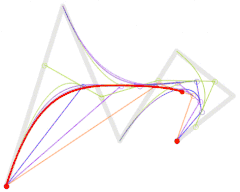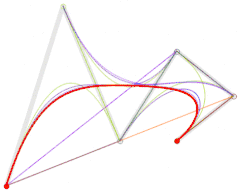 |
| رسم منحنى بيزيه من الدرجة الخامسة، حيث أن t تقع في الفترة [0,1]. |
لاحظ ان الفكرة في التوصل إلى رسم منحنى بيزيه، هي ان نقسم كل خط بوضع نقطة عليه ومن ثم نربط النقاط الجديدة مع بعضها البعض (لاحظ اننا نتخلص من نقطة في كل مرحلة), ونكرر العملية حتى يتبقى عندنا خط واحد فقط فنضع عليه (B(t ومن ثم نرسم المنحنى.
منحنيات بيزيه الحقيقية

يمكن اعتبار منحينات بيزيه الحقيقية مثل منحنيات بيزيه، الا ان الفرق بينهم هو وجود اوزان في منحنيات بيزيه الحقيقية، حيث يتم تزويد النقاط باوزان تؤثر على شكل المنحنى النهائي من اجل رسم الكثير من النماذج . و يمكن استخدامها في تمثيل اجزاء من قطع مخروطية بدقة، بما في ذلك اقواس دائرية(انظر الصورة الجانبية).
البسط هو نموذج بيرنشتاين لمنحنى بيزيه ويكون مصحوبا بالاوزان، اما المقام فهو المجموع المصحوب بالاوزان ل متعددة الحدود لبيرنشتاين, حيث يتم تمثيل المعادلة بالشكل التالي:
أو بطريقة أبسط:
على شكل متعددات الحدود
انظر إلى متعددة الحدود لبيرنشتاين.
انظر أيضا
مراجع
- "معلومات عن منحنى بيزيه على موقع vocab.getty.edu". vocab.getty.edu. مؤرشف من الأصل في 2020-01-26.
- "معلومات عن منحنى بيزيه على موقع britannica.com". britannica.com. مؤرشف من الأصل في 2015-09-10.
- "معلومات عن منحنى بيزيه على موقع rosettacode.org". rosettacode.org. مؤرشف من الأصل في 2019-04-02.
وصلات خارجية
- Cubic Bezier Curves: فيديو يبين كيف يقوم الحاسوب برسم منحنى بيزيه.
- بوابة تصميم
- بوابة رياضيات
- بوابة هندسة رياضية