معادلة تسالكوفسكي الصاروخية
معادلة تسالكوفسكي الصاروخية، أو معادلة الصاروخ المثالي (Tsiolkovsky rocket equation)، تصف حركة العربات التي تتبع المبدأ الأساسي للصاروخ: آلة قادرة على تزويد نفسها بالتسارع (كدفع) عبر نفث بعض كتلتها بسرعة عالية وتندفع بالتالي وفقا لمبدأ حفظ كمية الحركة. تربط المعادلة دلتا-في مع سرعة النفث الفعال والكتلة الابتدائية والنهائية للصاروخ (أو أي محرك رد فعلي).
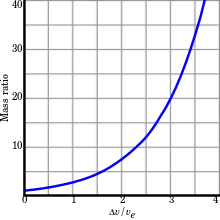
لأي قيادة من هذا النوع (أو رحلة تدخل فيها مراحل من هذه القيادة):
حيث:
- دلتا-في - التغير الأعظمي في السرعة للعربة (في غياب قوى خارجية مؤثرة).
- الكتلة الابتدائية متضمنة المادة الدافعة.
- الكتلة النهائية بدون المادة الدافعة، تعرف أيضا بالكتلة الجافة.
- سرعة النفث الفعالة.
- ترمز لدالة اللوغاريتم الطبيعي.
(يمكن أيضا كتابة المعادلة بدلالة الدفع النوعي بدلا من سرعة النفث بالصيغة حيث هو الدفع النوعي معبرا عنه بدلالة الزمن و الجاذبية القياسية ≈ 9.8 m/s2.)
الاشتقاق
باعتبار المنظومة:

في هذا الاشتقاق نشير بعبارة «الصاروخ» إلى «الصاروخ وكل مادته الدافعة غير المحترقة».
يربط قانون نيوتن للحركة بين القوى الخارجية () وبين التغير في الزخم الخطي للنظام ككل (بما في ذلك خرج أو نفث الصاروخ) كما يلي:
حيث هو كمية حركة الصاروخ عند زمن t=0:
و زخم الصاروخ والكتلة المنفوثة في زمن :
وحيث يكون بالنسبة للراصد:
سرعة الصاروخ في زمن t=0 سرعة الصاروخ في زمن سرعة الكتلة المضافة للنفث (وتفقد من قبل الصاروخ) خلال زمن كتلة الصاروخ في زمن t=0 كتلة الصاروخ في زمن
سرعة الخرج في إطار الراصد لها علاقة بسرعة الخرج في إطار الصاروخ بمقدار (حيث أن سرعة النفث في الاتجاه السالب)
ينتج الحل:
و باستعمال ، حيث أن إخراج كمية موجبة ينجم عنه نقصان في الكتلة،
في غياب القوى الخارجية تكون (حفظ كمية الحركة الخطية) و
بافتراض ثبات ، بالإمكان إجراء التكامل للحصول على:
أو بصورة مكافئة
- or or
حيث هي الكتلة الابتدائية الإجمالية متضمنة المادة الدافعة، الكتلة الإجمالية النهائية، و سرعة نفث الصاروخ نسبة إلى الصاروخ (الدفعة النوعي، أو إن قسناه زمنيا، يكون ذلك المضروب في تسارع الجاذبية).
القيمة تمثل إجمالي الكتلة المبددة وبالتالي:
حيث جزء كتلة المادة الدافعة (جزء من الكتلة الإجمالية الأولية التي أُنْفِقَت في صورة كتلة شغالة).
روابط خارجية
- بوابة الفضاء
- بوابة رحلات فضائية
- بوابة الفيزياء