مبرهنة كلفن-ستوكس

مبرهنة كلفن-ستوكس،[1][2] سميت نسبةً للرياضياتيين لورد كلفن وجورج ستوكس، معروفة أيضًا باسم مبرهنة ستوكس،[ملاحظة 1][3] أو المبرهنة الأساسية للدوران[ملاحظة 2] أو ببساطة مبرهنة الدوران،[ملاحظة 3][4] هي مبرهنة في حساب المتجهات على ${\displaystyle \mathbb {R} ^{3}}$. بالنظر إلى حقل متجهي، تربط المبرهنة تكامل دوران الحقل المتجهي على بعض السطح، بالتكامل الخطي للحقل المتجهي حول حدود السطح.

  ميّز عن مبرهنة ستوكس.

رسم توضيحي لمبرهنة كلفن-ستوكس، مع السطح Σ, وحدوده ∂Σ والمتجه الناظمي n.

جزء من سلسلة مقالات حول
التفاضل والتكامل
* المبرهنة الأساسية نهايات الدوال استمرارية مبرهنة القيمة المتوسطة مبرهنة رول تفاضل وتكامل كسري
حساب التفاضل اشتقاق حساب المتغيرات تفاضل ضمني مبرهنة تايلور معدلات مرتبطة متطابِقات قواعد قاعدة القوة قاعدة الضرب قاعدة ناتج القسمة قاعدة التسلسل قاعدة لايبنتز للتكامل
حساب التكامل تكامل قائمة التكاملات تكاملات معتلة تكامل ريمان تكامل متعدد التكامل بواسطة التجزئة الأقراص الطبقات الأسطوانية التعويض التعويضات المثلثية الكسور الجزئية تغيير الرتب
حساب المتسلسلات متسلسلة هندسية (حسابية هندسية) متسلسلة متناسقة متسلسلة متناوبة متسلسلة قوى متسلسلة ذو الحدين متسلسلة تايلور اختبارات التقارب اختبار الحد النوني اختبار النسبة اختبار الجذر اختبار التكامل للتقارب اختبار المقارنة اختبار مقارنة النهاية اختبار متسلسلة متناوبة اختبار التكثف لكوشي اختبار دركليه اختبار أبيل
حساب المتجهات تدرج تباعد دوران لابلاسي مبرهنة التدرج مبرهنة غرين مبرهنة ستوكس مبرهنة التباعد مبرهنة كلفن-ستوكس (مبرهنة الدوران)
حساب متعدد المتغيرات حسبان المصفوفات اشتقاق جزئي تكامل متعدد تكامل خطي تكامل سطحي تكامل حجمي جاكوبي
بوابة رياضيات

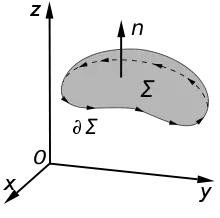
إذا كان الحقل المتجهي ${\displaystyle \mathbf {A} =(P(x,y,z),Q(x,y,z),R(x,y,z))}$ معرفة في منطقة ذات سطح أملس موجه ${\displaystyle \Sigma }$ وله مشتقات جزئية مستمرة من المرتبة الأولى، فإن:

${\displaystyle {\begin{aligned}\iint \limits _{\Sigma }(\nabla \times \mathbf {A} )\cdot d\mathbf {a} &=\iint \limits _{\Sigma }{\Bigg (}\left({\frac {\partial R}{\partial y}}-{\frac {\partial Q}{\partial z}}\right)\,dy\,dz+\left({\frac {\partial P}{\partial z}}-{\frac {\partial R}{\partial x}}\right)\,dz\,dx+\left({\frac {\partial Q}{\partial x}}-{\frac {\partial P}{\partial y}}\right)\,dx\,dy{\Bigg )}\\&=\oint \limits _{\partial \Sigma }{\Big (}P\,dx+Q\,dy+R\,dz{\Big )}=\oint \limits _{\partial \Sigma }\mathbf {A} \cdot d\mathbf {l} ,\end{aligned}}}$

حيث ${\displaystyle \partial \Sigma }$ هي حدود المنطقة ذات سطح أملس ${\displaystyle \Sigma }$.

يمكن ذكر مبرهنة كلفن-ستوكس الكلاسيكية المذكورة أعلاه في جملة واحدة: التكامل الخطي لحقل متجه على عُرْوة (Loop) يساوي تدفق دورانه عبر السطح المغلق.

مبرهنة كلفن-ستوكس هي حالة خاصة لمبرهنة ستوكس المعممة.[5][6] على وجه الخصوص، يمكن اعتبار حقل المتجه على ${\displaystyle \mathbb {R} ^{3}}$ أحادي الصورة وفي هذه الحالة يكون دورانه هو مشتقه الخارجي، ثنائي الصورة.