كارل فريدريش غاوس

يوهان كارل فريدريش غاوس (تلفظ بالألمانية: [kaʁl ˈfʁiːdʁɪç ˈɡaʊss]) [20] [21] (بالألمانية: Johann Carl Friedrich Gauß)، (باللاتينية: Carolus Fridericus Gauss) ولد في 30 أبريل/نيسان عام 1777 وتوفي في 23 فبراير/شباط عام 1855. كان رياضياتياً، وإحصائياً، وفيزيائياً، وعالماً ألمانياً. قدم مساهماتٍ هامّةً في العديد من المجالات في الرياضيات والعلوم.[22] يُشار إليه بلقب أمير علماء الرياضيات[23] (باللاتينية: Princeps mathematicorum)، أو أمير الرياضياتيين بفعل إنجازاته العلمية البارزة، وبـ«أعظم عالم رياضياتٍ منذ العصور القديمة»، وهو يرقى إلى سوية أكثر العقول تأثيراً في الرياضيات عبر التاريخ، بل اعتُبر واحداً من أهم ثلاثة علماءٍ في تاريخ الرياضيات.[هامش 1] ساهم بالكثير من الأعمال في نظرية الأعداد، والإحصاء، والتحليل الرياضي، والهندسة التفاضلية، والجيوديزيا، وعلم الاستاتيكا الكهربائية، وعلم الفلك، والبصريات، كما كان ذا تأثيرٍ استثنائيٍّ على العديد من المجالات الأخرى في الرياضيات والعلوم.[24] شمل نشاطه المجالات التطبيقية أيضاً، كمسح أراضي مملكة هانوفر، وكان أحد الرواد في اختراع التلغراف الكهرمغناطيسي مع ڤيلهلم إدوارد ڤيبر، كما طوّر مقاييس المغناطيسية وأسس شبكة عالمية من المحطات لدراسة المغناطيسية الأرضية.

كارل فريدريش غاوس
(بالألمانية: Carl Friedrich Gauß)‏ 
 
معلومات شخصية
اسم الولادة (بالألمانية: Johann Carl Friedrich Gauß)‏ 
الميلاد 30 أبريل 1777 [1][2][3][4][5][6][7] 
براونشفايغ[8][1][9] 
الوفاة 23 فبراير 1855 (77 سنة) [1][2][3][4][5][6][7] 
غوتينغن[8][1][10][11][12][9] 
مكان الدفن مقبرة ألباني ‏ 
الإقامة مملكة هانوفر
براونشفايغ 
مواطنة اتحاد الراين
مملكة هانوفر[13][14] 
عضو في الجمعية الملكية،  والأكاديمية الملكية السويدية للعلوم،  وأكاديمية العلوم في غوتينغن،  وأكاديمية سانت بطرسبرغ للعلوم ‏،  والأكاديمية المجرية للعلوم،  والأكاديمية الأمريكية للفنون والعلوم،  والأكاديمية البافارية للعلوم والإنسانيات،  والأكاديمية الروسية للعلوم،  والأكاديمية البروسية للعلوم،  والأكاديمية الملكية الهولندية للفنون والعلوم،  والأكاديمية الإيطالية للعلوم،  وأكاديمية تورين للعلوم[9] 
الأولاد
الحياة العملية
المدرسة الأم جامعة هلمشتيت
جامعة غوتينغن (1795–1798)
جامعة براونشفايغ التقنية 
شهادة جامعية دكتور في الفلسفة 
مشرف الدكتوراه يوهان فريدريش بفاف 
تعلم لدى يوهان كريستيان مارتن بارتلس 
طلاب الدكتوراه فريدريش بيسل،  وريتشارد ديدكايند،  وبرنارد ريمان،  وهاينريش كريستيان شوماخر،  وكريستيان لودفيج جيرلينج،  ويوهان بينيدكت ليستينغ،  وكارل جورج كريستيان فون شتاوت،  وصوفي جرمين،  وموريتز إبراهام شتيرن،  ويوهان إنكي 
التلامذة المشهورون فاركاس بولياي،  وأوغست فيرديناند موبيوس،  ويوهان بيتر غوستاف لوجون دركليه،  وغوستاف روبرت كيرشهوف،  وهاينريش كريستيان شوماخر 
المهنة رياضياتي[15]،  وعالم فيزياء الأرض،  وفلكي[16][17][18]،  وكاتب علم،  وفيزيائي[14]،  ومَسَّاح ‏،  وأستاذ جامعي،  وعالم إحصاء 
اللغات اللاتينية،  والألمانية،  والإنجليزية،  والفرنسية 
مجال العمل نظرية الأعداد،  والجبر،  وتحليل رياضي،  وهندسة تفاضلية،  وكهروستاتيكا،  وعلم البصريات،  ورياضيات،  وميكانيكا،  وعلم الفلك،  وعلم تقسيم الأرض،  وفيزياء،  وكهرومغناطيسية 
موظف في جامعة غوتينغن 
أعمال بارزة طريقة جاوس سيدل،  وقانون غاوس،  وقانون غاوس المغناطيسي،  وقانون غاوس للجاذبية ‏،  ووحدة غاوس،  وتوزيع احتمالي طبيعي 
الجوائز
التوقيع
 

سيرته الشخصية

السنوات المبكرة

ولد يوهان كارل فريدريش غاوس في الثلاثين من أبريل/نيسان من العام 1777 لأبوين فقيرين من الطبقة العاملة في منزلٍ يقع في 30 شارع ڤيلهلم بحي ڤندنغرابن Wendengraben في مدينة «برونزڤيك» (أو براونشڤايغ) في دوقية «برونزڤيك ولفنبوتل» (هي الآن جزء من ولاية «ساكسونيا السفلى» («صَاقِسُ السفلى») شمالي ألمانيا)،[25][26] حيث أنشئ لاحقاً متحف في الطابق الأرضي على شرفه إلا أنه لم بنجُ من دمار الحرب العالمية الثانية. زاول أبوه جِبهارد ديتريش غاوس (1744-1808) مهناً مختلفةً مثل بستانيٍّ وجزارٍ ومعاونٍ في متجرٍ وأمينِ صندوقٍ في شركة تأمينٍ صغيرةٍ، فيما كانت زوجته الثانية دوروثي بنتزي (1743-1839) خادمةً قبل الزواج وابنة حجّارٍ توفي مبكراً، لكنه وُصف بالذكاء وصفاء الذهن والشخصية الحازمة. بقيت علاقة غاوس بأمه وثيقةً على الدوام، وعاشت معه في منزله حتى توفيت في سن السادسة والتسعين. لم تسجلِ الوالدة الأميةً قطُّ تاريخَ ميلاده، بل تذكرت فقط أنه ولد يوم أربعاءٍ قبل ثمانية أيامٍ من «عيد الصعود» (والذي يحلُّ بعد تسعةٍ وثلاثين (39) يوماً من «عيد الفصح»). حلَّ غاوس هذا اللغز حول تاريخ ميلاده لاحقاً في سياق البحث عن تاريخ عيد الفصح، واشتقاق طرقٍ لحساب التواريخ للسنين الماضية واللاحقة.[27] جرى تعميده وتأكيده في كنيسةٍ بالقرب من المدرسة التي التحق بها فيما بعد حينما غدا في سن التعليم.[28]

تمثال غاوس في مسقط رأسه في برونزڤيك.
إنشاء مسدس منتظم بواسطة فرجار ومسطرة.

كان غاوس طفلاً نابغةً، وقد قال مازحاً عن نفسه فيما بعد إنه تعلم الحساب قبل أن يتكلم. كتب «ڤولفغانغ سارتوريوس فون ڤالترزهاوزن» في ذكرى غاوس أنه عندما كان بالكاد يبلغ من العمر ثلاث سنواتٍ قام عقلياً بتصحيح خطأٍ رياضيٍّ ارتكبه والده على الورق أثناء حساب موارده المالية، وأنه في سن التاسعةِ في مدرسة كاترينين العامة -بعد سنتين فقط من التحاقه بالمدرسة الابتدائية- حل مسألة متسلسلةٍ[هامش 2] حسابيةٍ أسرع بكثيرٍ من أي أحدٍ آخرَ في صفه البالغ مئة تلميذٍ.[29] ثمة روايات عديدة لهذه القصة مع تفاصيلَ مختلفةٍ حول طبيعة المتسلسلة، وأكثرها شيوعاً هي الإجابة عن السؤال التقليدي المتمثل بجمع الأعداد الصحيحة من الواحد إلى المئة.[30][31] [32] [هامش 3] هنالك العديد من الحكايات الأخرى حول نبوغه المبكر مذ كان يافعاً، ولقد قام بأول اكتشافاتٍ رياضياتيّةٍ رائدةٍ له وهو بعد في مرحلة المراهقة، وأكمل عمله العظيم «الاكتشافات الحسابية» (باللاتينية: Arithmeticae Disquisitiones) أو «التحقفات الحسابية» في العام 1798 في عمرٍ يناهز الحادية والعشرين (21)، والذي نُشر في العام 1801.[33] كان لهذا العمل دور أساسيٌّ في إرساء نظرية الأعداد كنظامٍ وتخصّصٍ في حد ذاته، وشكّلَ المجالَ حتى اليوم، ولا يزال تأثيره ملحوظاً إلى يوم الناس هذا.

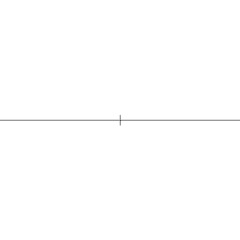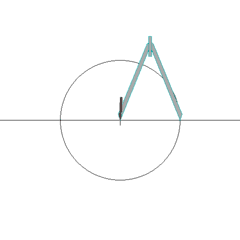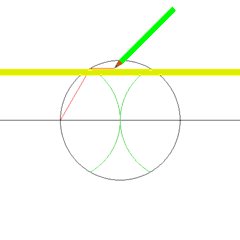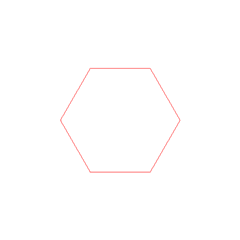
لفتت قدراتُ غاوسِ العقليةُ انتباه دوق برونزڤيك[30][24] الذي أرسله إلى «كلية كارل» (باللاتينية: Collegium Carolinum) (حالياً جامعة براونشفايغ للتقانة)، والتي التحق بها في الفترة (92-1795م)،[33] ومنها انتقل إلى جامعة غوتنغن ما بين العامين 1795 و1798.[33] وأثناء دراسته في الجامعة أعاد غاوس اكتشاف العديد من النظريات الهامة اكتشافاً مستقلاً. حدث اختراقه [أولى اكتشافاته] في العام 1796 عندما بيّنَ أن المضلع المنتظم يمكن إنشاؤه بفرجارٍ ومسطرةٍ (أداة يُختبَر بها استقامة الخط أو استواء المستوي) إذا كان عدد أضلاعه ناتجاً عن تربيع أعداد فيرما الأولية المختلفة (الرفع إلى الأس 2).[34][هامش 4] قرر غاوس من دون تقديم إثباتٍ أن هذا الشرط ضروري، لكنه لم ينشر برهانه مطلقاً.[هامش 5] كان هذا اكتشافاً كبيراً في حقلٍ هامٍّ من حقول الرياضيات؛ فقد شغلت مشاكل البناء علماء الرياضيات منذ أيام الإغريق القدماء، وأدى هذا الكشف في خاتمة المطاف إلى اختيار غاوس للرياضيات بدلاً من فقه اللغة كمهنةٍ، ولقد بلغ منه السرور بهذه النتيجة مبلغاً أنه طلب نقش شكل سُباعيِّ عشر الاضلاع على شاهدة قبره، لكن الحجّار رفض مشيراً إلى أن هذا البناء المعقد سيبدو أساساً كالدائرة.[35]

كان العام 1796 -وهو لما يزل في التاسعة عشرة- مثمراً لكلٍّ من غاوس ونظرية الأعداد. اكتشف إنشاء سُباعي عشر الأضلاع في الثلاثين من مارس/آذار،[33][36] كما قام بتطوير الحساب النمطي (بالإنجليزية: Modular arithmetic)‏، مما سهّل التعامل في نظرية الأعداد بشكلٍ كبيرٍ. في الثامن من أبريل/نيسان أضحى الرائدَ الذي أثبت قانون «التعاكس التربيعي» (بالإنجليزية: law of quadratic reciprocity)‏. يسمح هذا القانون -المعَمَّم بشكلٍ ملحوظٍ- للرياضياتيين بتحديد قابلية الحل لأي معادلةٍ من الدرجة الثانية في الحساب النمطي، كما تعطي نظرية الأعداد الأولية -التي أنهى صياغتها في الحادي والثلاثين (31) من مايو/أيار- فهماً جيداً لكيفية توزع الأعداد الأولية بين [مجموعة] الأعداد الصحيحة.

من يوميات غاوس حول مجموع الأعداد المثلثية (1796م).

اكتشف غاوس أيضاً أن بالإمكان تمثيل أي عددٍ صحيحٍ موجبٍ كمجموعٍ من ثلاثة أعدادٍ مثلثةٍ على الأكثر، وذلك في العاشر من يوليو/تموز، ثم دوّن في مذكراته الملاحظة التالية:
"ΕΥΡΗΚΑ! num = Δ + Δ + Δ"

وفي الأول من أكتوبر/تشرين الأول نشر نتيجةً عن عدد حلول كثيرات الحدود (بالإنجليزية: polynomials)‏ ذوات المعاملات (بالإنجليزية: coefficients)‏ التي تنتمي إلى الحقول المنتهية،[هامش 6] والتي أفضت بعد مئةٍ وخمسين عاماً إلى نظريات «ڤايل» (بالألمانية: Weil).

السنوات اللاحقة والوفاة

بقي غاوس نشطاً فكرياً إلى سن الشيخوخة حتى إبّانَ معاناته من التعاسة العامة ومرض النقرس،[37] وعلى سبيل المثال ففي عمر الثانية والستين (62) علّم نفسه بنفسه اللغة الروسية.[37] واحتفظ بموهبة إجراء أكثر الحسابات تعقيداً في ذهنه حتى بعدما طَعن في السن.

أصبح في العام 1807 مديراً لمرصد غوتنغن، وصاغ طريقة المربعات الصغرى، وفي العام 1840 نشر كتابه المؤثر «بحوث الانكسار» (باللاتينية: Dioptrische Untersuchungen)،[38] والذي قدم فيه أول تحليلٍ منهجيٍّ لتشكيل الصور في ظل التقريب شبه المحوري (البصريات الغاوسية).[39] أظهر غاوس من ضمن نتائجه أنه في ظل التقريب شبه المحوري يمكن تمييز النظام البصري بنقاطه الأساسية،[40] واشتق صيغة العدسة الغاوسية.[41]

في العام 1821 أضحى غاوس عضواً أجنبياً في «الأكاديمية الملكية السويدية للعلوم»، كما جرى انتخابه كذلك عضواً فخرياً أجنبياً في «الأكاديمية الأمريكية للفنون والعلوم» في العام 1822.[42] وفي العام 1845 أضحى عضواً منتسباً في «المعهد الملكي الهولندي»، وعندما تحول المعهد إلى «الأكاديمية الملكية الهولندية للفنون والعلوم» في العام 1851 انضم إليه كعضوٍ أجنبيٍّ.[43]

غاوس على فراش الموت (23 /2/ 1855).

ثم انتخب عضواً في «الجمعية الفلسفية الأمريكية» في العام 1853،[44] وفي العام 1854 اختار غاوس موضوع المحاضرة الافتتاحية لبرنارد ريمان (26-1866) «حول الفرضيات التي تقوم عليها الهندسة» (بالألمانية: Über die Hypothesen، welche der Geometrie zu Grunde liegen).[45] ذكر ڤيبر (بالألمانية: Weber) أن غاوس في طريق العودة إلى المنزل من محاضرة ريمان كان مليئاً بالثناء والإثارة.[46][هامش 7]

أمضى غاوس قُرابة الخمسين عاماً الأخيرة من حياته في مدينة غوتنغن التي كانت تابعةً لمملكة هانوفر وقتذاك، والتابعة لولاية "ساكسونيا السفلى" حالياً، وفي الثالث والعشرين (23) من فبراير/شباط من العام 1855 وعلى إثر نوبةٍ قلبيةٍ أسلم الروحَ،[25][47] وفي مقبرة سانت ألباني في غوتنغن رقد جسده رقدته الأخيرة. أبّنه في جنازته شخصان؛ خَتَنُه (زوج ابنته) "هاينريش إيڤالد"، و"ولفغانغ سارتوريوس فون ڤالترزهاوزن" صديق غاوس المُقرّب ومُدّونُ سيرته الذاتية. جرى الحفاظ على دماغ غاوس، ثم دراسته من قبل "رودولف ڤاجنر"، الذي وجد أن كتلته أكبر بقليلٍ من المتوسط؛ ألفٌ وأربعمئةٍ واثنان وتسعون (1492) غراماً (ما يعادل 52.6 أونصة)، ومساحة لحاء الدماغ تساوي 219.588 ملم مربع (ما يعادل 340.362 بوصة مربعة)، لكن تلافيف الدماغ كانت عالية التطور أيضاً، وقد افتُرض أن ذلك تفسيرٌ لعبقريته في أوائل القرن العشرين.[48]

آراؤه الدينية
جزء من سلسلة مقالات حول
الهندسة الرياضية
الفروع
  • المبادئ
  • الخواص
صفري الأبعاد
وحيد البعد
المُسطَّحات
المثلثات
متوازيات الأضلاع
رباعيات الأضلاع
المنحنيات
المُجسَّمات
ما فوق البعد الثالث
علماء الهندسة
وفق الاسم
وفق الحقبة
قبل الميلاد
1–1400م
1400–1700م
1700–1900م
معاصرون
 بوابة هندسة رياضية

كان غاوس عضواً اسمياً في كنيسة القديس ألباني الإنجيلية اللوثرية في غوتنغن.[49] وقد وصف جي. والدو دَنينغتون -أحدُ كتاب سيرته الذاتية- آراءَه الدينية على النحو التالي:[50]

«كان العلم بالنسبة إليه وسيلةً لكشف النواة الخالدة للروح البشرية. في أيام قوته الكاملة قدّم [العلم] له الترفيهَ، ومن خلال الآفاق التي فتحها له قدم العزاء، وقرب نهاية حياته جلب له الثقة. لم يكُ إله غاوس نسجاً بارداً وبعيداً عن الميتافيزيقيا، ولم يكن صورةً هزليةً [كاريكاتوريةً] مشوهةً للاهوت المرارة. لا يُؤمن للإنسان أن ملء المعرفة الذي من شأنه أن يبرر إصراره بغطرسةٍ على أن رؤيته غير الواضحة هي النور الكامل، وأنه لا يمكن أن يكون هناك أي شخصٍ آخر في مُكنته أن ينقل الحقيقة مثلما يفعل هو. بالنسبة إلى غاوس لا يقبل من يتغاضى عن عقيدته بل من يحياها. كان يعتقد أن الحياة التي تُعاش هنا على الأرض هي الأفضل، والوحيدة للاستعداد للسماء. الدين ليس مسألة أدبٍ، بل مسألة حياة. إن وحي الله مستمر، ولا يرد في ألواحٍ من الحجر أو من المخطوطات المقدسة. كتاب مستوحىً عندما يكون مصدر إلهامٍ. وإن الفكرة الراسخة المتمثلة في الاستمرارية الشخصية بعد الموت، والإيمان الراسخ بمنظمٍ أخيرٍ للأشياء، في إلهٍ أبديٍّ، عادلٍ، كليِّ العلمِ، كليِّ القدرةِ شكلت أساس حياته الدينية التي تنسجم تماماً مع بحثه العلمي.»

وإذا ما أغضينا الطرف عن مراسلاته، فليس ثمة تفاصيلُ كثيرةٌ معروفةٌ حول معتقدات غاوس الشخصية، ويختلف العديد من كتّاب سيرته حول رؤاه الدينية، فقد اعتبره بوهلر وآخرون ربّانياً مع وجهاتِ نظرٍ غيرِ تقليديةٍ (أو غير قويمةٍ) للغاية،[51] «أخبر غاوس صديقه "رودولف ڤاغنر" -أستاذ علم الأحياء بجامعة غوتنغن- أنه لا يؤمن تماماً بالكتاب المقدس، ولكنه كثيراً ما تأمّلَ في مستقبل الروح البشرية، وتكهّنَ بإمكانية تجسد الروح مرةً أخرى في كوكبٍ آخر. من الواضح أن غاوس كان ربانياً، وأن لديه قدراً كبيراً من الريبة فيما يتعلق بالدين، إلا أنه كان ينضوي على قدرٍ كبيرٍ من الاهتمام الفلسفي بالأسئلة الكبيرة، أي خلود الروح، والآخرة، ومعنى وجود الإنسان...» [52]

«كانت معتقدات غاوس الدينية مرتبطة وثيقاً بآرائه السياسية والاجتماعية. وعلى الرغم من معتقداته الدينية، ومن جذوره القوية في عصر التنوير فإته لم يكُ ملحداً، بل ربانياً مع قناعاتٍ غير تقليديةٍ للغاية؛ غير تقليديةٍ حتى مع مقارنتها بالمعتقدات الليبرالية جداً للكنيسة البروتستانتية المعاصرة.»[53] [54] بينما يشير دَنينغتون إلى أن غاوس كان على الأقل لوثرياً اسمياً معترفاً بأنه لم يك يؤمن حرفياً بجميع العقائد المسيحية، وأنه كذلك غير معروفٍ ما يعتقده في معظم الأسئلة العقائدية والطائفية:[55]

«لم يك معروفاً بالضبط ما يعتقده غاوس في معظم الأسئلة العقائدية والطائفية، فهو لم يكُ يؤمن حرفياً بجميع العقائد المسيحية. رسمياً كان عضواً في كنيسة سانت ألبانز (الإنجيلية اللوثرية) في غوتنغن. جميع طقوس التعميد، والدفن، وحفلات الزفاف كما أنه من غير المعروف ما إذا كان يحضر الكنيسة بانتظامٍ أو يساهم مالياً. دعاه جميع زملائه في الكلية مؤمناً (بالإنجليزية: deist)‏، ولكن ثمة سبب وجيه للاعتقاد بأن هذه التسمية لم تك ملائمةً بالشكل المناسب. امتلك غاوس تسامحاً دينياً قوياً إزاء كل معتَقَدٍ ناشئٍ في أعماق قلب الإنسان، إلا أنه لا ينبغي الخلط بين هذا التسامح واللامبالاة الدينية. لقد اهتم اهتماماً خاصّاً بالتطور الديني للجنس البشري، ولا سيّما في قرنه. وبالإشارة إلى الطوائف التي لم تتفق في كثيرٍ من الأحيان مع آرائهِ شدّد دائماً على أنه ليس ثمة ما يُسوّغ للمرء تعكير صفو إيمان الآخرين الذين يجدون فيه العزاء من المعاناة الدنيوية وملاذاً آمناً في أيام المحنة.»
مدفن غاوس في مقبرة القديس ألباني في غوتنغن - ألمانيا.

ثمة سجل لمحادثةٍ بين رودولف ڤاغنر وغاوس حول هذا ناقشا فيها كتاب «ويليام ڤيويل» عن تعدد العوالم. في هذا العمل تجاهل ڤيويل إمكانية وجود حياةٍ على كواكبَ أخرَ على أساس الحجج اللاهوتية، لكن ڤاغنر وغاوس كانا يختلفان مع هذا الموقف. أوضح ڤاغنر لاحقاً أن غاوس لم يكن يؤمن تماماً بالكتاب المقدس رغم اعترافه بأنه «يغبط» أولئك الذين يستطيعون الإيمان بسهولةٍ.[51] [55] عن هذا النقاش يورد دَنينغتون كلام غاوس لڤاغنر:

«أعتقد أنك تؤمن بالكتاب المقدس أكثرَ مني، أنا لست كذلك"، وأضاف: "مع التعبير عن المشاعر الداخلية الكبيرة فأنت أكثر سعادةً مني. يجب أن أقول بأنه كثيراً جداً في الأوقات السابقة عندما كنت أرى أناساً من الطبقات الدنيا، عمالٌ يدويون بسطاء ممن يمكنهم أن يؤمنوا بتوافقٍ حقٍّ مع قلوبهم، كنت أغبطهم دائماً"، ثم تابع بصوتٍ ناعمٍ، وبتلك الطريقة الطفولية الساذجة الخاصة به فيما دمعةٌ تترقرق في عينه: الآن قل لي كيف يشرع المرء في [مثل] ذلك؟..."}} أدى هذا فيما بعد إلى مناقشة موضوع الإيمان، وفي بعض الملاحظات الدينية الأخرى، قال غاوس إنه تأثر بعلماء اللاهوت مثل الوزير اللوثري «بول إرهارد» أكثر من تأثره [بالنبي] موسى. وشملتِ التأثرات الدينية الأخرى «ڤيلهلم براوباخ» (بالألمانية: Braubach)، و«يوهان بيتر زوسميلش»، والعهد الجديد. وثمة عملان دينيان قرأهما غاوس بشكلٍ متكررٍ هما «تعليم الأرواح» (بالألمانية: Seelenlehre) ل«براوباخ» (غيسن، 1843)، و«حفظ النظام الإلهي» ل«زوسميلش» (1756)، كما كرس وقتاً طويلاً للعهد الجديد باللغة اليونانية الأصلية.»[56]

ويشرح دَنينغتون مزيداً من التفاصيل حول آراء غاوس الدينية في هذا المقطع:[49]

«استند وعي غاوس الديني إلى التعطش النهم للحقيقة، والشعور العميق بالعدالة التي تمتد إلى السلع الفكرية والمادية على حدٍّ سواءٍ. لقد تصوّرَ الحياة الروحية في الكونِ كلِّه كنظامٍ قانونيٍّ عظيمٍ يخترقه الحق الأبدي، ومن هذا المصدر اكتسب ثقةً راسخةً بأن الموتَ لا يُنهي كلَّ شيءٍ.»

كان غاوس يؤمن بمصدرٍ للخلق كليِّ العلم، لكنه قال إن وجودَ [هذا] الاعتقادِ أو عدمِه لم يؤثرْ على رياضياته.[57] وعلى الرغم من أنه لم يكُ مرتاداً للكنيسة،[58] ولقد أيّدَ بشدةٍ التسامحَ الديني معتقداً بأنه «لا مُسوّغ للمرء لتعكير صفو المعتقدِ الديني للآخر، حيث يجدُ العزاءَ للأحزان الدنيوية في وقتِ الضيق».[24] وعندما أعلن ابنه إيوجين عن رغبته في أن يغدوَ مبشراً مسيحياً وافق على ذلك قائلاً: "إنه بغض النظر عن المشاكل داخل المنظمات الدينية، فإن العمل التبشيري كان مهمةً «مُشرِّفةً للغاية»".[24]

عائلته

أبوه «غِبهارد ديتريش غاوس» المولود عام 1744 والمتوفى في 14 أبريل/نيسان من العام 1808، وأمه «دوروثي بنتزي» ولدت في العام 1743، وتوفيت في 18 أبريل/نيسان من العام 1838، وكان له أخ أكبر غير شقيقٍ من زواجٍ سابقٍ لأبيه.

في التاسع من أكتوبر/تشرين الأول من العام 1805 تزوج غاوس من جوان أوستهوف (1780-1809)،[59] وأنجب منها ولدين وبنتاً. توفيت جوان في الحادي عشر من أكتوبر/تشرين الأول من العام 1809،[59][60][61] بعد نحو خمسة أشهرٍ من إنحابها، وتوفي ابنهما الأصغر لويس في العام التالي ولما يتجاوز عامه الأول،[59] وغرق غاوس في انهيارٍ عصبيٍّ لم يتعافَ منه نهائياً. ثم تزوج من «مينا ڤالدِك» (1788-1831)[59][60] في الرابع من أغسطس/آب من العام 1810،[59] التي أنجبت له ثلاثة أطفالٍ آخرين.[60] لم يعد غاوس مثلما كان من بعد وفاة زوجته الأولى، ومثل والده تماماً كبر كي يُهيمنَ على أطفاله. توفيت مينا ڤالدِك في الثاني عشر من سبتمبر/أيلول من العام 1831.[59][60]

خلّف غاوس ستةَ أطفالٍ؛ من جوان (1780-1809) كان لديه جوزيف (06-1873)، وڤلهيلمينا (08-1846)، ولويس (09-1810). ومن «مينا ڤالدِك» كان لديه ثلاثة أيضاً: إيوجين (11-1896)، وڤلهلم (13-1879)، وتريز (16-1864). وُهبَ إيوجين مستوىً جيداً من موهبة أبيه كارل في اللغات والحساب.[62] تولت تيريز -بعد وفاة زوجته الثانية في العام 1831- إدارة المنزل، واهتمت بأبيها لبقية حياته، ولم تتزوج إلا بعد وفاته. عاشت والدة غاوس معه في منزله من العام 1817 وحتى وفاتها في العام 1839.[24]

واجه غاوس في النهاية صراعاتٍ مع أبنائه. لم يكن يريد لأحدٍ منهم الانخراط في سلك دراسة الرياضيات أو العلوم «خوفاً من تراجع اسم العائلة»، فقد رأى أن أيّاً منهم لن يتفوقَ على إنجازاته.[62] أراد غاوس من إيوجين أن يصبح محامياً، لكن إيوجين أراد دراسة اللغات، وقد خاضا جدالاً حول حفلةٍ أقامها إيوجين، ورفض غاوس دفع تكاليفها. وغادر الابن المنزلَ مُغضَباً، وهاجر حوالي العام 1832 إلى الولايات المتحدة. وأثناء عمله في شركة American Fur Company في الغرب الأوسط تعلم لغة «السو» (بالإنجليزية: Sioux)‏، وفي وقتٍ لاحقٍ انتقل إلى ولاية ميسوري وأضحى رجلَ أعمالٍ ناجحاً. انتقل ڤلهلم أيضاً إلى أمريكا في العام 1837، واستقر في ميسوري كذلك حيث بدأ كمزارعٍ، ثم أصاب لاحقاً ثروةً من تجارة الأحذية في سانت لويس. استغرق نجاح إيوجين سنواتٍ عديدةً كي يبطل سمعته [التي لحقته] بين أصدقاء كارل غاوس وزملائه. (انظر أيضاً رسالة روبرت غاوس إلى فيليكس كلاين في الثالث من سبتمبر/أيلول 1912).

ثيريز ابنة غاوس (18–1864).

زوجتاه:

  • «اليزابيث جوانا روزينا أوستوف»، ولدت في 8 مايو/أيار عام 1780، وتوفيت في 11 أكتوبر/تشرين الأول عام 1809، تزوج من جوانا في 9 أكتوبر/تشرين الأول عام 1805، وتوفيت بعد خمسة أشهرٍ من ولادة ابنهما الثالث لويس، وأصيب غاوس إثر وفاتها بانهيارٍ عصبيٍّ لم يشفَ منه تماماً.
  • «فريدريكا فليلمنين ڤالدِك»؛ ولدت في 15 أبريل/نيسان عام 1788، وتوفيت في 12 سبتمبر/أيلول عام 1831 بعد صراعٍ طويلٍ مع المرض، عُرفت باسم «مينا»، وكانت أفضلَ صديقةٍ لزوجته الأولى. تزوجها في 4 أغسطس/آب عام 1810.

أطفاله: لغاوس ستة أطفال:

  • من جوانا:
  • جوزيف: ولد 21 أغسطس/أب عام 1806، وتوفي 4 يوليو/تموز 1873.
  • ڤلهيلمينا: ولدت 29 فبراير 1808، توفيت في 12 أغسطس/آب عام 1840، تزوجت في العام 1830 من «هاينريش أيڤالد». كانت -من بين جميع أطفال غاوس- موهوبةً، لكنها توفيت شابة.
  • لويس: ولد في 10 سبتمبر/أيلول عام 1809، وتوفي في 1 مارس/أذار عام 1810.
  • من مينا:
  • إيوجين: ولد في 29 يوليو/تموز عام 1811، وتوفي في 4 يوليو/تموز عام 1896.
  • ڤلهلم: ولد في 23 أكتوبر/تشرين الأول عام 1813، وتوفي في 23 أغسطس/أب عام 1879.
  • تريز: ولدت في 9 يونيو/حزيران عام 1816، وتوفيت في 11 فبراير/شباط عام 1864.

شخصيته وآراؤه
كارل فريدريش جاوس بريشة «كريستيان ألبريشت جنسن» (1840)، مرصد بولكُڤو.
ثمة اقتباس من اختيار غاوس تحت اللوحة من مسرحية «الملك لير» لشكسبير: «أنت، الطبيعة، فن العراقة؛ لقوانينك مكرسةٌ خدماتي»:
«Thou, nature, art my goddess; to thy laws my services are bound»

كان غاوس من المتحمسين للكمال والعمل الشاق. لم يك مطلقاً كاتباً غزير الإنتاج، فقد رفض نشر عملٍ ما لم يره كاملاً وفوق النقد، وكان هذا تماشياً مع شعاره الشخصي: «قليل، لكن ناضج» (باللاتينية: pauca sed matura). تشير مذكراته الشخصية إلى إنجازه العديدَ من الاكتشافات الرياضياتية المهمة قبل سنواتٍ أو عقودٍ من نشرها من قبل معاصريه. قال عالم الرياضيات والكاتب الإسكتلندي الأمريكي «إريك تمبل بيل»: «لو أن غاوس نشر جميع اكتشافاته في الوقت المناسب، لكان تقدمَ بالرياضياتِ خمسين عاماً».[63]

وعلى الرغم من أنه قبل عدداً قليلاً من الطلبة [في حياته]، إلا أته كان معروفاً بكرهه للتدريس، ويُقال إنه حضر مؤتمراً علمياً واحداً فقط، وذلك في برلين في العام 1828. وقد غدا العديد من طلبته رياضياتيين بارزين ومؤثرين، ومن بينهم «ريتشارد ديديكيند»، و«برنارد ريمان»، و«فريدريش بيسل».

وبناءً على توصيةٍ من غاوس مُنح «فريدريش بيسل» (بالألمانية: Bessel) درجة الدكتوراة الفخرية من جامعة غوتنغن في مارس/آذار من العام 1811،[هامش 8] وفي ذلك الوقت تقريباً انخرط الرجلان في المراسلات،[64] ومع ذلك فعندما التقيا شخصياً في العام 1825 تشاجرا، لكن تفاصيلَ ذلك غيرُ معروفةٍ.[65] وأوصى غاوس لصوفي جيرمان قبل وفاتها بدرجةٍ فخريةٍ لكنها لم تتلقها قط.[66]

يرفض غاوس -عادةً- تقديم الحدس الكامن وراء براهينه الأنيقة جداً في كثيرٍ من الأحيان، لقد فضّل اتبثاقَها «من فراغٍ»، ومحوَ كافة آثار كيفية اكتشافه لها. كان هذا مُسوَّغاً من قبل غاوس -وإن يكُ غيرَ مُرضٍ- فقد ذكر في كتابه «الاكتشافات الحسابية» (باللاتينية: Disquisitiones Arithmeticae) أن جميع التحليلات (أي المسارات) -التي يسافر المرء عبرها للوصول إلى حل مشكلةٍ ما- يجب قمعُها من أجل الإيجاز.

دعم غاوس النظام الملكي وعارض نابليون (1769-1821م) الذي اعتبره ثمرةً للثورة [الفرنسية] وامتداداً لها.[هامش 9]

لخص غاوس رُؤاه حول السعي في سبيل المعرفة في رسالةٍ إلى «فاركاس بولياي» بتاريخ الثاني من سبتمبر/أيلول من العام 1808 على النحو التالي:[67]

«إنها ليستِ المعرفة ولكن فعل التعلم، وليس التملك بل عملية الوصول إلى هناك هي ما تمنح أكبر قدْرٍ من المتعة. عندما أكون أوضحت واستنفدت موضوعاً ما، فإني أبتعد عنه لأذهب إلى الظلمة مرةً أخرى. الرجل الذي لا يرضى مطلقاً غريبٌ جداً. إذا كان قد أكمل بناءً، فلن يكون من أجل السكنى فيه بسلامٍ، ولكن من أجل البدء بآخرَ. أتخيل أن فاتح العالم يجب أن يشعر بذلك، إن المرء -بعدما ينتهي من غزو مملكةٍ ما- نادراً ما يفتح ذراعيه للآخرين.»

لقد نوّه إلى الرياضيات على أنها «ملكة العلوم»[68] ويُفترَض أنه اعتقد ذات مرةٍ اعتقاداً بضرورة الفهم الفوري لـ«هوية أويلر» كمعيارٍ بناءً على أنه أضحى عالم رياضياتٍ من الدرجة الأولى.[69]

حياته المهنية وإنجازاته

الجبر
صفحة العنوان لعمل غاوس الكبير "التحققات الحسابية"، أو "الاكتشافات الحسابية".

في رسالة الدكتوراة في العام 1799 -وفي غياب برهانٍ جديدٍ على النظرية القائلة بأن كل دالّةٍ جبريّةٍ جذريّةٍ كاملةٍ لمتغيرٍ واحدٍ يمكن حلها إلى عواملَ حقيقيّةٍ من الدرجة الأولى أو الثانية- أثبت غاوس النظريةَ الأساسيةَ للجبر والتي تنص على أن كل دالةٍ (تابعٍ) غير ثابتةٍ كثيرة الحدود لمتحولٍ واحدٍ وذاتِ معاملاتٍ عُقَدِيّةٍ لها جذرٌ عُقَدِيٌّ واحدٌ على الأقل. كان علماء الرياضيات بمن فيهم «جان لو روند دالمبرت» قد قدموا أدلةً خاطئةً من قبل، وقد احتوت أطروحة غاوس على نقدٍ لعمل «دالمبرت». ومن المفارقات -وفقاً لمعايير اليوم- أن محاولةَ غاوس الخاصةَ غيرُ مقبولةٍ بسبب الاستخدام الضمني لنظرية منحني «جوردان»، ومع ذلك فقد قدم -فيما بعد- ثلاثة أدلةٍ أخرى كان آخرها -في عام 1849- بليغاً بشكلٍ عامٍّ. أوضحت محاولاته مفهوم الأعداد المركبة بشكلٍ كبيرٍ على طول الخط.

قدم غاوس أيضاً مساهماتٍ مهمةً في «نظرية الأعداد» من خلال كتابه «التحققات الحسابية» (باللاتينية: Arithmeticae Disquisitiones) في العام 1801، قدم الكتاب -من بين قضايا أخرى- رمز الشريط الثلاثي (≡) للتطابق، واستخدمه في عرضٍ واضحٍ للحساب النمطي، كما احتوى على أول إثباتين لقانون «التعاكس التربيعي» (بالإنجليزية: law of quadratic reciprocity)‏، وطور نظريات الأشكال التربيعية الثنائية والثلاثية، وذكر مشكلة عدد الصنف بالنسبة لها، وبيّن كذلك أنه يمكن بناء مضلعٍ سُباعَ-عشريٍّ منتظمٍ (مضلعٌ ذو سبعة عشر (17) جانباً) باستخدام المسطرة والفرجار. ويبدو أن غاوس كان يعرف بالفعل صيغة عدد الصنف في العام 1801.[70]

بالإضافة إلى ذلك فقد أثبت النظريات التخمينية التالية:

  • نظرية عدد فيرما للمضلع لـ n = 3.
  • نظرية فيرما الأخيرة لـ n = 5.
  • قاعدة ديكارت للإشارات.
  • نظرية كبلر للترتيبات المنتظمة.

وأيضاً:

  • شرح الخماسي (انظر موقع جامعة بيليفيلد).
  • طور خوارزمية لتحديد تاريخ عيد الفصح.
  • اخترع خوارزمية Cooley-Tukey FFT لحساب تحولات فورييه المنفصلة قبل مئةٍ وستين (160) عاماً من كولي وتوكي.

الفلك
طالع أيضًا: مربعات دنيا ومبرهنة غاوس-ماركوف
صورة شخصية لغاوس نُشرت في مجلة الأخبار الفلكية في العام 1828.

في الأول من يناير/كانون الثاني من العام 1801 اكتشف عالم الفلك الإيطالي «جوزيبي بيازي» الكوكب القزم «سيريس»، وتمكن من تقصّي مساره إلى حدٍّ ما لما يزيد عن شهرٍ، وتتبعه حتى زاوية ثلاث درجاتٍ [عبر مداره] في سماء الليل قبل أن يختفيَ مؤقتاً خلف وهج الشمس، وبعد عدة أشهرٍ وحيثما كان من المفترض ظهوره مجدداً لم يتمكن بيازي من تحديد موقعه. لم تكنِ الأدوات الرياضية ذلك الوقت بقادرةٍ على استقراء موضعٍ بمثل هذه الكمية الضئيلة من البيانات (تمثل ثلاث درجاتٍ أقل من 1 ٪ من مدار الكوكب).[هامش 10] سمع غاوس بالمشكلة وعمل على معالجتها، وعقِبَ ثلاثةِ أشهرٍ من العمل المكثف توقع موقع «سيريس» في ديسمبر/كانون الأول من العام 1801 بعد نحو عامٍ من رؤيته لأول مرةٍ، واتضح أن هذا كان دقيقاً بدقة نصف درجةٍ وذلك عندما أعاد «فرانز اكزافير فون زاخ» اكتشافه في 31 ديسمبر/كانون الأول في «غوتا» (بالألمانية: Gotha)، وبعد ذلك بيومٍ واحدٍ من قبل «هاينريش أولبرز» في بريمن.[33] أدى هذا التأكيد في الختام إلى تصنيف «سيريس» على أنه كوكبٌ صغيرٌ. كان «سيريس 1» أول كُويْكبٍ جرى اكتشافه على الإطلاق (حالياً يسمى كوكب قزم [كُويْكِب]).[71][72]

تضمنت طريقة غاوس تحديدَ مقطعٍ مخروطيٍّ في الفضاء مع إعطاء تركيزٍ [لمركزٍ] واحدٍ (الشمس) وتقاطع المخروط مع ثلاثةِ خطوطٍ معينةٍ وفي الوقت المحدد (خطوط الرؤية من الأرض إلى الكويكب والتي [أخذاً بالاعتبار] تتحرك هي نفسها على شكلٍ بيضاويٍّ). يأخذ الكويكب باجتياز الأقواس التي تحددها هذه الخطوط (يمكن حساب أطوال الأقواس التي تحددها هذه الخطوط بواسطة قانون كبلر الثاني). تُفضي هذه المشكلة إلى معادلةٍ من الدرجة الثامنة يُعرف حلٌّ واحدٌ منها وهو مدار الأرض، ثم يجري فصل الحل المطلوب عن الحلول الستة [المجهولة] المتبقية بناءً على الظروف المادية. استخدم غاوس -في هذا العمل- طرق التقريب الشاملة التي ابتكرها لهذا الغرض.[73] وكانت إحدى هذه الطرق هي ما يُعرف اليوم بتحويل فورييه السريع.

وفي حين تُنسب هذه الطريقة إلى ورقةٍ من العام 1965 كتبها جيمس كولي وجون توكي،[74] فإن غاوس كان قد طورها كطريقة استيفاءٍ مثلثيٍّ. نُشرت ورقته البحثية هذه «طريقة جديدة لنظرية الاستيفاء»[75] بعد وفاته فقط [ت. 1855] في المجلد الثالث من أعماله التي جرى جمعها. تسبق هذه الورقة أول عرضٍ قدمه جوزيف فورييه حول هذا الموضوع في العام 1807.[76]

نتيجة الإسقاط الشكلي لمجموعة نقاطٍ (الحمراء) على دالّةٍ (تابعٍ) من الدرجة الثانية، حيث "خط الانحدار" (الأزرق) هو الخط الذي يحقق أصغر مجموعٍ لمربعات الفروق بين القيم الحقيقية (أو المرصودة /المشاهََدة /المَقيسة) والقيم المحسوبة رياضياتياً والممثَّلة بخط الانحدار. وإذا كان هذا هو شرط خط الانحدار الذي يُنشأ غلى أساسه (وهو المجموع الأصغري لمربعات الفروق)، فإن خط الانحدار لا يُشترط فيه أن يمرَّ بجميع النقاط الحقيقية أو ببعضِها، كما يمكن ألا يمر بأيٍّ منها.

ومع أن غاوس كان -حتى تلك اللحظة- مدعوماً مالياً براتبه من الدوق، إلا أنه كان متشككاً في أمان هذا الترتيب، ولم يك أيضاً يعتقد أن الرياضياتِ البحتةَ مهمة بما يكفي لاستحقاق الدعم، وهكذا سعى للحصول على منصبٍ في علم الفلك، وفي العام 1807 عُيّن أستاذاً لعلم الفلك ومديراً للمرصد الفلكي في غوتنغن، وهو المنصب الذي شغله طيلة الفترة المتبقية من حياته.

نوّه «زاخ» إلى أنه «لولا العمل الذكي وحسابات الدكتور غاوس لما وجدنا سيريس مرة أخرى»، وقد قاد اكتشاف «سيريس» إلى عمل غاوس على نظرية حركة الكواكب التي تؤثر (تُشوّش) عليها الكواكب الكبيرة، والتي نُشرت في النهاية في العام 1809 كنظريةٍ لحركة الأجرام السماوية في المقاطع المخروطية المحيطة بالشمس (نظرية حركة الأجرام السماوية تتحرك في مقاطعَ مخروطيةٍ حول الشمس). في هذه العملية قام بتبسيط الرياضيات المرهقة في القرن الثامن عشر للتنبؤ المداري [لحركة الكواكب] لدرجة أن عمله لا يزال يشكل حجر الزاوية في الحساب الفلكي.[77] وقدّم ثابت الجاذبية الغاوسي الذي احتوى على معالجةٍ مؤثرةٍ لطريقة المربعات الصغرى، وهو الإجراء المستخدم في جميع العلوم حتى يومنا هذا لتقليل تأثير خطأ القياس.[هامش 11]

أثبت غاوس هذه الطريقة استناداً إلى الافتراض بأن الأخطاءَ موزعةٌ بشكلٍ طبيعيٍّ (انظر نظرية "غاوس-ماركوڤ"؛ وانظر أيضاً الغاوسية). وُصفت هذه الطريقة مسبقاً من قبل «أدريان-ماري ليغندر» (1752-1833) (بالفرنسية: Adrien-Marie Legendre)‏ في العام 1805، لكن غاوس زعم أنه كان يستخدمها منذ العام 1794 أو 1795.[78] وفي تاريخ الإحصاء يُطلق على هذا الخلاف تسمية «نزاع الأولوية حول اكتشاف طريقة المربعات الصغرى».[79]

المسح الجيوديزي
حجر علامة مساحي في غارلستي (حالياً غارلشتاد).

في العام 1818 وضع غاوس مهاراتِه الحسابيّةَ موضعَ الاستخدامِ العملي، وأجرى مسحاً جيوديزياً لمملكة هانوفر (مسح الأراضي الغاوسي [الألماني])، بالربط مع المسوحات الدنماركية السابقة. اخترع -للمساعدة في المسح- جهاز هليوتروب غاوس (بالإنجليزية: Gauss heliotrope)‏، وهي أداة تستخدم مرآةً لعكس ضوء الشمس على مسافاتٍ كبيرةٍ لقياس المواضع.

ظهر ورقة عشر ماركات ألمانية (1993) تظهر الهليوتروب (بالإنجليزية: heliotrope)‏ وقسماً من شبكة المسح المثلثاتية التي نفذها غاوس واستخدم فيها ذلك الجهاز.

في العام 1828 وعند دراسة الاختلافات في خط العرض حدد غاوس -لأول مرةٍ- تقريباً مادياً لشكل الأرض حيث إن سطح الأرض في كل مكانٍ متعامد مع اتجاه الجاذبية (التي يشكل متوسط مستوى سطح البحر جزءاً منها)، والتي دعيت فيما بعد بالحيود.[80]

الهندسات غير الإقليدية

ادعى غاوس أيضاً أنه اكتشف إمكانية وجود هندسات غير إقليديةٍ لكنه لم ينشرها مطلقاً. كان هذا الاكتشاف نقلةً نوعيةً كبيرةً في الرياضيات، لأنه حرر علماء الرياضيات من الاعتقاد الخاطئ بأن بدهيّات إقليدس كانتِ الطريقة الوحيدة لجعل الهندسة متسقةً وغير متناقضةٍ.

فيما بعد قاد البحث في هذه الهندسات -من بين أمورٍ أخرى- إلى نظرية أينشتاين في النسبية العامة التي تصف الكون بأنه غير إقليدي. حاول صديقه «فاركاس وولفغانغ بولياي» (بالإنجليزية: Bolyai)‏ -الذي أقسم غاوس معه على «الأخوة وراية الحقيقة» عندما كانا طالبين- عبثاً لسنواتٍ عديدةٍ إثبات بدهية التوازي من بدهيات الهندسة الأخرى لإقليدس.

اكتشف «يانوس بولياي» -ابن فاركاس بولياي- الهندسة غير الإقليدية في العام 1829؛ ونُشر عمله في العام 1832. وبعد اطلاعه عليه كتب غاوس إلى «فاركاس بولياي»: «إن الثناء عليه يرقى إلى مدح نفسي. بالنسبة إلى محتوى العمل بأكمله ... [فهو] يتطابق تماماً -تقريباً- مع تأملاتي الخاصة التي شغلت ذهني خلال الثلاثين أو الخمس والثلاثين سنةً الفائتة». هذا التصريح غير المؤكد أوجد ضغطاً على علاقته مع بولياي الذي اعتقد أن غاوس كان «يسرق» فكرته.[81]

تكشف رسائل غاوس قبل العام 1829 أنه يناقش بشكلٍ غامضٍ مشكلة الخطوط المتوازية، ويجادل والدو دَنينغتون -كاتب سيرة غاوس- في [كتابه] «غاوس، تيتان العلم» (بالإنجليزية: Gauss، Titan of Science)‏ (1955) أن غاوس كان -في الواقع- يمتلك الهندسة اللاإقليدية قبل وقتٍ طويلٍ من نشرها بواسطة بولياي، لكنه رفض نشر أيٍّ منها بسبب خشيته من الجدل.[82][83]

نظرية ممتازة

تطلب المسح الجيوديزي لمملكة هانوفر من غاوس قضاء الصيف في التنقل على ظهور الجياد لمدة عقدٍ من الزمن[84] وغذّى اهتمامه بالهندسة التفاضلية والطوبولوجيا، ومجالات الرياضيات التي تتعامل مع المنحنيات والأسطح. جاء غاوس -من بين أمورٍ أخرى- بمفهوم «الانحناء الغاوسي»، وأدى ذلك في العام 1828 إلى نظريةٍ مهمةٍ (باللاتينية: Theorema Egregium) (نظرية رائعة)، والتي أسست خاصية مهمة لمفهوم الانحناء حيث تقرر -بشكلٍ غير رسميٍّ- إنه يمكن تحديد انحناء السطح بالكامل عن طريق قياس الزوايا والمسافات على السطح، ما يعني أن الانحناء لا يعتمد على كيفية دمج السطح في فضاءٍ ثلاثي الأبعاد أو فضاءٍ ثنائي الأبعاد.

المغناطيسية

في العام 1831 طور غاوس تعاوناً مثمراً مع أستاذ الفيزياء «ڤيلهلم ڤيبر» مما أدى إلى معارفَ جديدةٍ في المغناطيسية (بما في ذلك العثور على تمثيل لوحدة المغناطيسية من حيث الكتلة والشحنة والزمن)، واكتشاف قوانين دارات كيرشهوف في الكهرباء.[47] أثناء ذلك الوقت قام بصياغة قانونٍ يحمل الاسم نفسه. قام العالمان ببناء أول تلغرافٍ كهروميكانيكيٍّ في العام 1833،[85] والذي ربط المرصد بمعهد الفيزياء في غوتنغن. أمر غاوس ببناء مرصدٍ مغناطيسيٍّ في حديقة المرصد، وأسس مع ڤيبر «الجمعية المغناطيسية» (بالألمانية: Magnetischer Verein)، والتي دعمت قياسات المجال المغناطيسي للأرض في العديد من مناطق العالم. طور طريقةً لقياس الشدة الأفقية للمجال المغناطيسي، والتي كانت قيد الاستخدام بشكلٍ جيدٍ حتى النصف الثاني من القرن العشرين، ووضع النظرية الرياضياتية لفصل مصادر (الغلاف المغناطيسي) الداخلية والخارجية للمجال المغناطيسي للأرض.

كما استنبط حلاً للمعادلات ذات الحدين وأثبت قانون التبادل التربيعي، مثلما أسس النظرية الرياضية للكهرباء، ثم أطلق اسمه على الوحدة الكهرومغناطيسية المستخدمة لقياس الحث (الحفز) المغناطيسي غاوس وتساوي 1 ماكسويل على السنتيمتر المربع.[86]

الاحتمالات والتوزيع الاحتمالي الطبيعي
المقالة الرئيسة: توزيع احتمالي طبيعي
التوزيع الطبيعي المعياري: توزيع طبيعي نفترض فيه ترتيب المتوسط يساوي الصفر على المحور الأفقي. في هذا التوزيع تتساوى قيم "المتوسط الحسابي" و"الوسيط" و"المنوال". إحدى خصائص هذا التوزيع أن القيمَ الأصغرَ من انحرافٍ معياريٍّ واحدٍ عن المتوسط الحسابي (بالإنجليزية: Mean)‏ (والذي يساوي مجموع القيم مقسوماً على عددها) تمثل نسبةَ 68.27٪ من مجموع قيم الظاهرة (المجال ما بين القيمتين - ، + على المحور الأفقي، وتمثل هذه النسبة المساحة المحصورة ما بين المنحني والمحور الأفقي)؛ بينما يمثل ضعفا الانحراف المعياري عن الوسط نسبة 95.45٪؛ وثلاثة انحرافاتٍ معياريّةٍ عن الوسط تمثل نسبة 99.73٪ من مجموع القيم.
حيث: M = المتوسط الحسابي، = الانحراف المعياري.

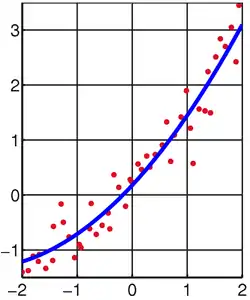
في العام 1733 وضع أبراهام دي مواڤر (1667-1754) (بالفرنسية: De Moivre)‏ نطريته الأولى حول التوزيع الطبيعي والتي عُرفت بالمنحني الأسي ذي شكل الجرس (بالإنجليزية: Exponential bell-shaped Curve)‏ بناءً على التقريب التقديري الذي توصل إليه من نظرية احتمال رمي القطع المعدنية عدة مراتٍ وتوزيعها. في العام 1809 وبعد دراساته حول طريقة المربعات الصغرى قام غاوس بإطلاق نظريته الهامة عن التوزع الاحتمالي الطبيعي، والتي دعاها «التوزيع الطبيعي» (بالإنجليزية: Normal distribuition)‏ حيث استفاد منها في حساب توقع مواقع الأجرام الفلكية. ومذ ذاك الحين أخذ هذا التوزيع أهميته وانتشاره، وعُرف أيضاً باسم «التوزيع الغاوسي»، كما اشتُهر المنحني البياني الذي يمثل هذا التوزيع باسم «منحني الجرس» (بالإنجليزية: Bell Curve)‏.[هامش 12]

تقييم
أربعة توزيعاتٍ طبيعيةٍ.

أورد عالم الرياضيات البريطاني «هنري جون ستيفن سميث» (26-1883) التقييم التالي عن كارل غاوس:[87]

«إذا ما استثنينا الاسم العظيم لنيوتن، فلربما من المحتمل ألا يتفوق أي عالم رياضياتٍ من أي عصرٍ أو بلدٍ على غاوس في الجمع بين خصوبةٍ وفيرةٍ للابتكار مع صرامةٍ مطلقةٍ في البرهان، وهو ما قد يغبطه عليه الإغريق أنفسهم. قد يبدو الأمر متناقضاً، ولكن ربما يكون صحيحاً -مع ذلك- أن الجهودَ التي بُذلت بعد الكمال المنطقي للشكل هي التي جعلت كتابات غاوسَ مفتوحةً لتهمة الغموض والصعوبة غير الضرورية. يردد غاوس أكثر من مرةٍ أنه بهدف الإيجاز يقدم فقط التوليف، ويمنع تحليل مقترحاته.[هامش 13] من ناحيةٍ أخرى إذا ما عدنا إلى مذكرات أويلر (07-1783م) فثمة نوع من الرشاقة الحرة والفاخرة حول الأداء بأكمله، والتي تُخبر عن المتعة الهادئة التي على أويلر أن ينالها في كل خطوةٍ من عمله. ليست أقل ادعاءاتِ غاوس بنيل إعجاب علماء الرياضيات أنه على الرغم من اختراقه بالكامل بالإحساس باتساع العلم، فقد فرض أقصى درجات الصرامة في كل جزءٍ منه، ولم يتجاوز قط صعوبةً كما لو أنها غير موجودةٍ، ولم يقبلِ البتة نظريةً ما على أنها صحيحةٌ بما يتجاوزِ الحدودَ التي يمكن من خلالها البرهنة عليها بالفعل.»

تكريمه وإحياء ذكراه
المقالة الرئيسة: قائمة المواضيع المنسوبة إلى كارل فريدريش غاوس
ورقة مالية ألمانية من فئة عشرة ماركاتٍ ألمانيةٍ (تاريخ 1 سبتمبر/أيلول عام 1999) تُظهر صورة غاوس، وبعض مباني غوتنغن، ومنحني التوزيع الطبيعي على خلفيتها.

من العام 1989 وإلى العام 2001 ظهرت صورة غاوس، ومنحني التوزيع الطبيعي، وبعض مباني غوتنغن البارزة على الأوراق النقدية الألمانية من فئة عشرة ماركات. أصدرت دائرة البريد الألمانية الغربية أيضاً ثلاثة طوابعَ بريديةٍ تكريماً لغاوس. أحدها (رقم 725) في العام 1955 في الذكرى المئوية الأولى لوفاته، والاثنان الآخران (رقم 1246، و1811) في العام 1977 تخليداً للذكرى المئوية الثانية لمولده.

في العام 2007 جرى نصب تمثالٍ نصفيٍّ لغاوس في معبد والْهالا. (بالإنجليزية: Walhalla)‏.[88]

كما قامت جامعة غوتينغن بالتنسيق والتعاون مع مدينة غوتينغن و«جمعية غاوس» بالاحتفال بعام غاوس في العام 2005، وشمل الاحتفال معارضَ وسلسلةً من المحاضرات والجولات ومهرجان النجوم.

غاوس في الأدب والفن

انظر أيضًا

هوامش
  1. بالإضافة إلى أرخميدس ونيوتن.
  2. المتسلسلة أو السلسلة الرياضية (بالإنجليزية: Series)‏ هي عددٌ متتالٍ من الحدود ينتج أحدها عن الحد الذي قبله بقانونٍ معين، ومجموعها هو مجموع هذه الحدود. ربما تكون هذه الحدود أعداداً أو دالاتٍ، وربما يكون عددها منتهياً (محدوداً) أو لا منتهٍ. يدعى (an) الحد العام أو الحد النوني.
  3. أرجح الروايات حول الحادثة أن أستاذه بوتنر اعتاد تكليف تلامذته بمسائلَ للحل أثناء الدرس، وربما كي يشغلهم عن الشغب، وذات مرةٍ طلب منهم أن يجمعوا الأعداد من الواحد إلى المئة. لم يتوانَ غاوسُ ذو الأعوام التسعةِ سوى ثوانٍ عن إعطاء الإجابة الصحيحة ما أدهش الأستاذ ومساعده مارتن بارتلز. لقد رتب في ذهنه الأرقامَ على شكل مجاميعَ متساويةٍ لثنائياتٍ متتاليةٍ قائمةٍ على الجمع الحسابي كما يلي:
    عددعمليةعددنتيجة
    1+100= 101
    2+99= 101
    3+98= 101
    ...+...= 101
    ...+...= 101
    49+52= 101
    50+51= 101
    ومنه استنتج أن المجموع المتكرر (101) مضروباً بخمسين (عدد الثنائيات) يعطي (50 * 101 = 5050) هو المجموع المطلوب. للقصة رواياتٌ مختلفةُ التفاصيلِ بحسب "وولفغانغ سارتوريوس فون ڤالترزهاوزن" حتى إن أحد المؤلفين المُحْدثين "جوزيف روتمان" في كتابه "دورة أولى في الجبر المجرد" (2000م) شكّك في حدوثها أصلاً، لكنها متداولة. يطلق اليوم على طريقة الحساب هذه "معادلة تجميع غاوس".
  4. القوة في المصطلح الرياضياتي تتألف من عددين؛ أساسٍ وأسٍّ؛ مثال: 32 نقول عن 3 الأساس، وعن 2 الأس. إن التعبيرَ الشائعَ الرفع إلى قوةٍ خطأ لأن القوة هي مجمل العددين مرتبين وفق الشكل الأسي المبين، والصواب القول الرفع إلى أس.
  5. فيما بعد قدّم بيير ڤانتزل برهاناً كاملاً على هذا الشرط.
  6. نقول عن عدة حدودٍ في تركيبٍ جبريٍّ إنها تؤلف كثيرَ حدودٍ (أو متعدد حدودٍ) إذا كان الذي يربط فيما بينها هو الجمع الجبري (بمعنى الجمع والطرح)، أما المعاملات فتترابط فيما بينها بعملية الضرب. مثلاً في متعدد الحدود التالي:

    نقول عن 3 و5- و4 عوامل، وعن (X1 * 5) حد.
  7. تقوم الهندسة الإقليدية على مُسَلّماتِ إقليدسَ الخمسِِ ومنها المُسَلّمةِ الأشهرُ في عالم الرياضيات؛ «من نقطةٍ خارجَ مستقيمٍ يمكن إنشاءُ مستقيمٍ واحدٍ موازٍ لذلك المستقيمِ الأول، وهذا المستقيم وحيد».
    لكن ريمان -الذي كان أحد طلبة غاوس النجباء- استناداً إلى الافتراض بأنه «من نقطةٍ خارج مستقيمٍ يمكن إنشاءُ أكثرَ من مستقيمٍ واحدٍ موازٍ لذلك المستقيم الأول» أسس هندسةً خاصةً («هندصة ريمان») مختلفةً عن الهندسة الإقليدية. فيما بعد أثبتت «هندصة ريمان» جدواها غندما اعتمد أينشتاين بين 1911 و1916 عليها في تطوير نظريته من النسبية الخاصة إلى النسبية العامة والبرهان عليها.
  8. لم يتلقَّ فريدريش بيسل مطلقاً أي تعليمٍ جامعيٍّ في حياته.
  9. وكان هذا على النقيض تماماً من آراء معاصره لودڤيغ ڤان بيتهوفن (1770-1827) الذي كان معجباً جداً بنابليون، فلما أخبروه بإعلانه نفسه إمبراطوراً (عام 1804)، علق في خيبةِ أملٍ: "الآن أصبح رجلاً عادياً".
  10. قسمة ثلاثِ درجاتٍ على 360 درجةً تبلغ أقل من تسعةٍ بالألف: (360 / 3 < 9 بالألف) وتمثل أقل من واحدٍ بالمئة من إجمالي المدار.
  11. يُفترض في الخط الذي يمثل رياضيّاتباً مجموع المشاهدات (أو القياسات) أن يكون أقربَ ما يكون إلى هذه المشاهدات، وعليه تقوم "طريقة المربعات الصغرى" أو الدنيا (بالإنجليزية: Least squares)‏ في الإحصاء على التقليل من مجموع الفروق بين القيم الفعلية والقيم المحسوبة رياضياتباً إلى أقل حدٍّ ممكنٍ [تؤخذ مربعات الفروق لجعل القيم جميعاً موجبة، وإلغاء التقاصّ عند الجمع بين القيم السالبة (عندما تكون القيم الفعلية أكبر من القيم النظرية) والقيم الموجبة (حيث القيم الفعلية أصغر من القيم النظرية)].
    يُستفاد من "طريقة المربعات الصغرى" لتقدير "خط الانحدار" (أو الخط الممثل للبيانات) وهو الخط الذي يؤدي إلى تقليل مجموع الانحرافات (أو الأخطاء الاحتمالية) الرئيسة الواردة في النقاط التي جرت ملاحظتها وتسجيلها، بمعنى يجري تقليص مجموع مربعات الفروق بين كلٍّ من القيم الفعلية والقيم المحسوبة رياضياتياً إلى أدنى حد. يمكن القول أيضاً إنها طريقة تقريبٍ قياسيّةٍ تُستخدم لحل أنظمة المعادلات التي يكون فيها عدد المتغيرات أكبرُ من عدد المعادلات (من الناحية الرياضياتية بلزمنا عدد معادلاتٍ مساوٍ لعدد المتغيرات المجهولة (المتحولات) حتى يمكن إيجاد قيم جميع المتغيرات). تعني «المربعات الدنيا» بأن الحل الكلي (الذي يشمل جميع البيانات) يتجه نحو جعل قيمة مجموع مربعات الخطأ الناتج عن حل كل معادلةٍ أصغريّاً.
    أحد أهم تطبيقاتِ هذه الطريقة هو "الإسقاط الشكلي للبيانات" (بالإنجليزية: Data Fitting)‏ (المعنى الحرفي مواءمة البيانات). ويكون أفضلُ إسقاطٍ شكليٍّ لمجموعة بياناتٍ هو الذي ينحو باتجاه تصغير مجموع مربعات الأخطاء، حيث إن الخطأ هو "الفرق بين القيمةِ المقيسةِ [الفعليةِ] للبيانات والقيمةِ المُسقَطَةِ على الشكل الرياضياتي".
    يجدر التنويه إلى الخطأ في تسمية هذه الطريقة (بالإنجليزية: Least Squares)‏ فهي لا تعني "المربعات الصغرى"، بل بالأحرى -وبمعنىً أدقَّ- "المحموع الأصغر للمربعات". في جميع الأحوال إن طريقة توظيف غاوس لها مع الأدوات الرياضياتية الأخرى (كالتوزيع الطبيعي) في توقع مسار الكويكب "سيريس" لدليلٌ على مدى عبقريته.
  12. التوزيع الطبيعي (بالإنجليزية: Normal Distribuition)‏ هو توزيع احتمالي يستخدم لنمذجة ظواهر ذات سلوكٍ افتراضيٍّ معينٍ وانحرافاتٍ تراكميةٍ محتمَلةٍ عن هذا السلوك. فإذا كان من المتوقع -مثلاً- لرامٍ ماهرٍ أن تصيب سهامه حول الهدف، ومع ذلك -ونظراً لتراكم العيوب في أسلوب هذا الرامي- فإن معظم السهام ستخطئ عين الهدف ببعض المسافة. يُعرف "المتوسط الحسابي" (مجموع القيم مقسوماً على عددها) لهذه المسافة في الرماية بـ"الدقة" (بالإنجليزية: Accuracy)‏، بينما يُعرف مقدار التباين في المسافات بـ"الإحكام" أو "الضبط" (بالإنجليزية: Preciseness)‏. يُشار -في سياق "التوزيع الطبيعي"- إلى الدقة والإحكام بـ"المتوسط الحسابي" و"الانحراف المعياري" (بالإنجليزية: Standard Deviation)‏ على التوالي. وبذلك يمكن التعبير في مقياسٍ محدودٍ عن إتقان (كفاءة) رامي السهام بقيمتين؛ متوسطٍ وانحرافٍ معياريٍّ. تعني هاتان القيمتان -في التوزيع الطبيعي- أن ثمة احتمالاً بنسبة 68٪ تقريباً أن يهبط السهم ضمن انحرافٍ معياريٍّ واحدٍ لمتوسط دقة الرامي، واحتمالاً يصل إلى 95٪ تقريباً أن يهبط السهم في حدود انحرافين معياريين لمتوسط دقة الرامي، و99.7٪ تقريباً ضمن ثلاثة انحرافاتٍ معياريةٍ، وهكذا زيادةً ببطءٍ حتى 100٪.
  13. "التوليف" (بالإنجليزية: «Synderesis») أو (بالإنجليزية: «Synteresis»): في الفلسفة الأخلاقية هو القدرة الطبيعية أو تصرف العقل العملي بهدف فهم المبادئ العامة الأولى للفعل البشري بشكلٍ حدسيٍّ، والمقصود أنه يطرح استنتاجه الذي خلص إليه عن طريق الحدس دون تقديم البرهان.

مراجع
  1. verschiedene Autoren (1875), Historische Commission bei der königl. Akademie der Wissenschaften (ed.), Allgemeine Deutsche Biographie (بالألمانية), Leipzig: Duncker & Humblot, QID:Q590208
  2. تاريخ ماكتوتور لأرشيف الرياضيات، QID:Q547473
  3. RKDartists | Carl Friedrich Gauss (بالهولندية), QID:Q17299517
  4. Brockhaus Enzyklopädie | Carl Friedrich Gauß (بالألمانية), QID:Q237227
  5. Gran Enciclopèdia Catalana | Carl Friedrich Gauss (بالكتالونية), Grup Enciclopèdia, QID:Q2664168
  6. www.accademiadellescienze.it | Carl Friedrich Gauss (بالإيطالية), QID:Q107212659
  7. Proleksis enciklopedija | Carl Friedrich Gauss (بالكرواتية), QID:Q3407324
  8. А. М. Прохоров, ed. (1969), Большая советская энциклопедия: [в 30 т.] (بالروسية) (3rd ed.), Москва: Большая российская энциклопедия, Гаусс Карл Фридрих, OCLC:14476314, QID:Q17378135
  9. www.accademiadellescienze.it (بالإيطالية), QID:Q107212659
  10. http://www.tandfonline.com/doi/full/10.1080/00207160.2012.689826. {{استشهاد ويب}}: |url= بحاجة لعنوان (مساعدة) والوسيط |title= غير موجود أو فارغ (من ويكي بيانات) (مساعدة)
  11. http://www.tandfonline.com/doi/pdf/10.1080/00207160.2012.689826. {{استشهاد ويب}}: |url= بحاجة لعنوان (مساعدة) والوسيط |title= غير موجود أو فارغ (من ويكي بيانات) (مساعدة)
  12. http://onlinelibrary.wiley.com/doi/10.1002/2014JA019973/full. {{استشهاد ويب}}: |url= بحاجة لعنوان (مساعدة) والوسيط |title= غير موجود أو فارغ (من ويكي بيانات) (مساعدة)
  13. http://www.maa.org/publications/maa-reviews/50th-imo-50-years-of-international-mathematical-olympiads. {{استشهاد ويب}}: |url= بحاجة لعنوان (مساعدة) والوسيط |title= غير موجود أو فارغ (من ويكي بيانات) (مساعدة)
  14. (PDF) http://link.springer.com/content/pdf/10.1007%2F978-3-642-14565-0_3.pdf. {{استشهاد ويب}}: |url= بحاجة لعنوان (مساعدة) والوسيط |title= غير موجود أو فارغ (من ويكي بيانات) (مساعدة)
  15. http://www.nndb.com/lists/776/000105461/. {{استشهاد ويب}}: |url= بحاجة لعنوان (مساعدة) والوسيط |title= غير موجود أو فارغ (من ويكي بيانات) (مساعدة)
  16. http://onlinelibrary.wiley.com/doi/10.1002/wilm.10249/pdf. {{استشهاد ويب}}: |url= بحاجة لعنوان (مساعدة) والوسيط |title= غير موجود أو فارغ (من ويكي بيانات) (مساعدة)
  17. http://onlinelibrary.wiley.com/doi/10.1111/j.1600-0498.1998.tb00422.x/pdf. {{استشهاد ويب}}: |url= بحاجة لعنوان (مساعدة) والوسيط |title= غير موجود أو فارغ (من ويكي بيانات) (مساعدة)
  18. http://www.jstor.org/stable/2332332. {{استشهاد ويب}}: |url= بحاجة لعنوان (مساعدة) والوسيط |title= غير موجود أو فارغ (من ويكي بيانات) (مساعدة)
  19. "Award winners : Copley Medal" (بالإنجليزية). Royal Society. Retrieved 2018-12-30.
  20. Dudenredaktion; Kleiner, Stefan; Knöbl, Ralf (2015) [First published 1962]. Das Aussprachewörterbuch [The Pronunciation Dictionary] (بالألمانية) (السابعة ed.). برلين: Dudenverlag. pp. 246, 381, 391. Archived from the original on 2021-10-07. {{استشهاد بكتاب}}: الوسيط غير المعروف |الرفم المعياري= تم تجاهله (help)
  21. Krech, Eva-Maria; Stock, Eberhard; Hirschfeld, Ursula; Anders, Lutz Christian (2009). Deutsches Aussprachewörterbuch [German Pronunciation Dictionary] (بالألمانية). برلين: Walter de Gruyter. pp. 402, 520, 529. Archived from the original on 2021-11-29.
  22. "Gauss, Carl Friedrich". Encyclopedia.com. مؤرشف من الأصل في 2022-01-25. {{استشهاد ويب}}: الوسيط غير المعروف |تاريخ الدخول= تم تجاهله (مساعدة)
  23. Zeidler، Eberhard (2004). Oxford Users' Guide to Mathematics. Oxford، المملكة المتحدة: دار نشر جامعة أكسفورد. ص. 1188.
  24. Dunnington، Waldo (1927). "The Sesquicentennial of the Birth of Gauss". Scientific Monthly. ج. 24 رقم  5. ص. 402–414. Bibcode:1927SciMo..24..402D. JSTOR:7912. مؤرشف من الأصل في 2008-02-26.{{استشهاد بمجلة}}: صيانة الاستشهاد: BOT: original URL status unknown (link) متوفر أيضاً على "The Sesquicentennial of the Birth of Gauss". مؤرشف من الأصل في 2023-02-19. Retrieved 23 February 2014. Comprehensive biographical article.
  25. "Carl Friedrich Gauss". Wichita State University. مؤرشف من الأصل في 2021-10-09.
  26. Cayley 1911.
  27. "Mind Over Mathematics: How Gauss Determined The Date of His Birth". مؤرشف من الأصل في 2022-02-06. {{استشهاد ويب}}: الوسيط غير المعروف |موقع ويب= تم تجاهله (مساعدة)
  28. Susan Chamberless (11 مارس 2000). عنوان= Letter:WORTHINGTON,_Helen_to_Carl_F._Gauss_-_1911-07-26 "Letter:WORTHINGTON, Helen to Carl F. Gauss – 26 July 1911". Susan D. Chambless. اطلع عليه بتاريخ 2011-09-14. {{استشهاد ويب}}: تحقق من قيمة |مسار= (مساعدة)
  29. Waltershausen, Wolfgang Sartorius von (1856), Gauss zum Gedächtniss (بالألمانية), S. Hirzel, p. 12, Archived from the original on 2021-05-01
  30. Bruno 2003، صفحة 178.
  31. "Gauss, Carl Friedrich (1777–1855)." (2014). In The Hutchinson Dictionary of scientific biography. Abington, United Kingdom: Helicon.
  32. Hayes، Brian (2006). "Gauss's Day of Reckoning". American Scientist. ج. 94 رقم  3. ص. 200. DOI:10.1511/2006.59.200. مؤرشف من الأصل في 2012-01-12. اطلع عليه بتاريخ 2012-10-30.
  33. Bruno 2003، صفحة 179.
  34. "نسخة مؤرشفة". مؤرشف من الأصل في 2021-12-14. اطلع عليه بتاريخ 2022-02-28.{{استشهاد ويب}}: صيانة الاستشهاد: BOT: original URL status unknown (link)
  35. Pappas, Theoni ‏, Mathematical Snippets, 2008, p. 42. "نسخة مؤرشفة". مؤرشف من الأصل في 2021-12-14. اطلع عليه بتاريخ 2022-02-28.{{استشهاد ويب}}: صيانة الاستشهاد: BOT: original URL status unknown (link)
  36. Carl Friedrich Gauss §§365–366 in استفسارات حسابية. Leipzig, Germany, 1801. New Haven, CT: مطبعة جامعة ييل, 1965.
  37. Bruno 2003، صفحة 181.
  38. Bühler 1981، صفحات 144-145.
  39. Hecht، Eugene (1987). Optics. Addison Wesley. ص. 134. مؤرشف من الأصل في 2022-03-08.
  40. Bass، Michael؛ DeCusatis، Casimer؛ Enoch، Jay (2009). Handbook of Optics. McGraw Hill Professional. ص. 17.7. {{استشهاد بكتاب}}: الوسيط |الأول4= يفتقد |الأخير4= (مساعدة) والوسيط |مؤلف4-الأول= و|الأول4= تكرر أكثر من مرة (مساعدة)
  41. Ostdiek، Vern J.؛ Bord، Donald J. (2007). Inquiry into Physics. Cengage Learning. ص. 381. مؤرشف من الأصل في 2022-04-10.
  42. "Book of Members, 1780–2010: Chapter G" (PDF). American Academy of Arts and Sciences. مؤرشف من الأصل (PDF) في 2016-10-14. اطلع عليه بتاريخ 2016-09-08.
  43. "C.F. Gauss (1797–1855)". Royal Netherlands Academy of Arts and Sciences. مؤرشف من authorDetail&aId= PE00000342 الأصل في 2023-02-19. اطلع عليه بتاريخ 2015-07-19. {{استشهاد ويب}}: تحقق من قيمة |مسار= (مساعدة)
  44. "APS Member History". search.amphilsoc.org. مؤرشف من الأصل في 2021-04-17. اطلع عليه بتاريخ 2021-04-16.
  45. Monastyrsky، Michael (1987). Riemann, Topology, and Physics. Birkhäuser. ص. 21–22.
  46. Bühler 1981، صفحة 154.
  47. Bruno 2003، صفحة 181.
  48. Bardi، Jason (2008). The Fifth Postulate: How Unraveling A Two Thousand Year Old Mystery Unraveled the Universe. John Wiley & Sons, Inc. ص. 189.
  49. Dunnington 2004، صفحة 300.
  50. harvnb & Dunnington 2004، صفحات 298–301.
  51. Bühler 1981، صفحة 153.
  52. Gerhard Falk (1995). American Judaism in Transition: The Secularization of a Religious Community. University Press of America. ص. 121. مؤرشف من الأصل في 2020-08-01. أخبر غاوس صديقه "رودولف ڤاغنر" -أستاذ علم الأحياء بجامعة غوتنغن- أنه لا يؤمن تماماً بالكتاب المقدس، ولكنه كثيراً ما تأمّلَ في مستقبل الروح البشرية، وتكهّنَ بإمكانية تجسد الروح مرةً أخرى في كوكبٍ آخر. من الواضح أن غاوس كان ربانياً، وأن لديه قدراً كبيراً من الريبة فيما يتعلق بالدين، إلا أنه كان ينضوي على قدرٍ كبيرٍ من الاهتمام الفلسفي بالأسئلة الكبيرة، أي خلود الروح، والآخرة، ومعنى وجود الإنسان...
  53. بمعنى أن معتقداتِ غاوسَ الدينيةَ كانت غيرَ تقليديةٍ ليس فحسب بالنسبة إلى عصرها (عصر التنوير) الميال إلى العقل على حساب الدين، وإنما كذلك بالمقارنة مع المواقف الليبرالية جداً للكنيسة البروتستانتية.
  54. Bühler 1981، صفحة 152: كانت معتقدات غاوس الدينية مرتبطة ارتباطاً وثيقاً بآرائه السياسية والاجتماعية. وعلى الرغم من معتقداته الدينية، ومن جذوره القوية في عصر التنوير إلا أته لم يكُ ملحداً، بل ربانياً مع قناعاتٍ غير تقليديةٍ للغاية؛ غير تقليديةٍ حتى مع مقارنتها بالمعتقدات الليبرالية للغاية للكنيسة البروتستانتية المعاصرة.
  55. harvnb & Dunnington 2004، صفحة 305.
  56. Dunnington 2004، صفحة 305.
  57. موريس كلين (1982). Mathematics: The Loss of Certainty. مطبعة جامعة أكسفورد. ص. 73. مؤرشف من الأصل في 2021-09-01.
  58. "Gauss, Carl Friedrich". Complete Dictionary of Scientific Biography. 2008. مؤرشف من الأصل في 2016-09-29. اطلع عليه بتاريخ 2012-07-29. في تناقضٍ ظاهريٍّ اتجهت آراؤه الدينية والفلسفية إلى آراء خصومه السياسيين. لقد كان مؤمناً -بلا هوادةٍ- في أولوية "التجريبية" في العلم. لم يلتزم بآراء كانط وهيجل وغيرهما من الفلاسفة المثاليين في ذلك الوقت، ولم يكن رجلَ كنيسةٍ واحتفظ بآرائه الدينية لنفسه. كانتِ الاستقامة الأخلاقية وتقدم المعرفة العلمية من مبادئه المعلنة.
  59. "Person:GAUSS, Carl Friedrich (1777–1855) – Gauss's Children". gausschildren.org (بالإنجليزية). Archived from the original on 2021-05-25. Retrieved 2017-12-10.
  60. Bruno 2003، صفحة 180.
  61. "Johanna Elizabeth Osthoff 1780–1809 – Ancestry". www.ancestry.com (بالإنجليزية الأمريكية). Archived from the original on 2020-12-02. Retrieved 2017-12-10.
  62. "Letter: Charles Henry Gauss to Florian Cajori – 21 December 1898". Susan D. Chambless. 11 مارس 2000. مؤرشف من الأصل في 2022-02-09. اطلع عليه بتاريخ 2011-09-14.
  63. Bell، E.T. (2009). "Ch. 14: The Prince of Mathematicians: Gauss". Men of Mathematics: The Lives and Achievements of the Great Mathematicians from Zeno to Poincaré [رجال الرياضيات: حيوات كبار الرياضياتيين وإنجازاتهم من زينون إلى بوانكاريه]. New York: Simon and Schuster. ص. 218–269.
  64. Helmut Koch, Introduction to Classical Mathematics I: From the Quadratic Reciprocity Law to the Uniformization Theorem, Springer, p. 90.
  65. Oscar Sheynin, History of Statistics, Berlin: NG Verlag Berlin, 2012, p. 88. نسخة محفوظة 8 مارس 2021 على موقع واي باك مشين.
  66. Mackinnon, Nick (1990). "Sophie Germain, or, Was Gauss a feminist?". The Mathematical Gazette 74 (470): 346–351, esp. p. 347.
  67. Dunnington 2004، صفحة 416.
  68. Quoted in Waltershausen, Wolfgang Sartorius von (1856, repr. 1965). Gauss zum Gedächtniss. Sändig Reprint Verlag H. R. Wohlwend. (ردمك 3-253-01702-8)
  69. Derbyshire، John (2003). Prime obsession : Bernhard Riemann and the greatest unsolved problem in mathematics. Washington, DC: Joseph Henry Press. ص. 202. مؤرشف من الأصل في 2020-08-01. اطلع عليه بتاريخ 2022-07-05. first-class mathematician.
  70. "Did Gauss know Dirichlet's class number formula in 1801?". MathOverflow. 10 أكتوبر 2012. مؤرشف من الأصل في 2022-01-16.
  71. Resnick, Brian (30 Apr 2018). "Johann Carl Friedrich Gauß was called "the prince of mathematics." Here's why". Vox (بالإنجليزية). Archived from the original on 2021-06-28. Retrieved 2020-09-01.
  72. Marsden، Brian G. (1 أغسطس 1977). "Carl Friedrich Gauss, Astronomer". Journal of the Royal Astronomical Society of Canada. ع. 71. ص. 309. Bibcode:1977JRASC..71..309M. ISSN:0035-872X. مؤرشف من الأصل في 2022-03-08.
  73. Klein، Felix؛ Hermann، Robert (1979). Development of mathematics in the 19th century. Math Sci Press.
  74. Cooley، James W.؛ Tukey، John W. (1965). "An algorithm for the machine calculation of complex Fourier series". Mathematics of Computation (Math. Comput.). ج. 19 رقم  90. ص. 297–301. DOI:10.2307/2003354. JSTOR:2003354.
  75. Gauss, C.F. (1876) [n.d.]. Theoria Interpolationis Methodo Nova Tractata (بلاتينية). Göttingen: Göttingen] K. Gesellschaft der Wissenschaften zu Göttingen. pp. 265–327. Archived from the original on 2020-08-01. {{استشهاد بكتاب}}: |عمل= تُجوهل (help)صيانة الاستشهاد: لغة غير مدعومة (link)
  76. Heideman، M.؛ Johnson, D.؛ Burrus, C. (1984). "Gauss and the history of the fast fourier transform" (PDF). IEEE ASSP Magazine. ج. 1 رقم  4. ص. 14–21. DOI:10.1109/MASSP.1984.1162257. S2CID:10032502. مؤرشف من الأصل (PDF) في 2022-03-07.
  77. Felix Klein, Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert. Berlin: Julius Springer Verlag, 1926.
  78. Oscar Sheynin, History of Statistics, Berlin: NG Verlag Berlin, 2012, p. 81. نسخة محفوظة 8 مارس 2021 على موقع واي باك مشين.
  79. Stephen M. Stigler, "Gauss and the Invention of Least Squares," Ann. Statist., 9(3), 1981, pp. 465–474.
  80. Gauß, C.F. (1828). Bestimmung des Breitenunterschiedes zwischen den Sternwarten von Göttingen und Altona durch Beobachtungen am Ramsdenschen Zenithsector (بالألمانية). Vandenhoeck und Ruprecht. p. 73. Archived from the original on 2021-11-23. Retrieved 2021-07-06.
  81. Steven G. Krantz (1 أبريل 2010). An Episodic History of Mathematics: Mathematical Culture through Problem Solving. MAA. ص. 171–. مؤرشف من الأصل في 2022-03-07. اطلع عليه بتاريخ 2013-02-09.
  82. Halsted، G.B. (1912). "Duncan M.Y. Sommerville". American Mathematical Monthly. ج. 19 رقم  1. ص. 1–4. DOI:10.2307/2973871. JSTOR:2973871.
  83. Sondow، J. (2014). "From the Monthly Over 100 Years Ago…". American Mathematical Monthly. ج. 121 رقم  10. ص. 963. arXiv:1405.4198. DOI:10.4169/amer.math.monthly.121.10.963. S2CID:119144776.jstor.org arXiv "Gauss and the eccentric Halsted".
  84. The Prince of Mathematics نسخة محفوظة 2020-09-18 على موقع واي باك مشين.. The Door to Science by keplersdiscovery.com.
  85. Bruno 2003، صفحة 181.
  86. Juha Pyrhönen؛ Tapani Jokinen؛ Valéria Hrabovcová (2009). Design of Rotating Electrical Machines. John Wiley and Sons. ص. 232. ISBN:0-470-69516-1. مؤرشف من الأصل في 2017-03-13.
  87. H.J.S Smith,Presidential Address, Proceedings of the London Math. Soc. VIII, 18.
  88. "Bayerisches Staatsministerium für Wissenschaft, Forschung und Kunst: Startseite" (PDF). Stmwfk.bayern.de. مؤرشف من الأصل (PDF) في 2009-03-25. اطلع عليه بتاريخ 2009-07-19.
  89. baharuka (25 أكتوبر 2012). "Die Vermessung der Welt". Internet Movie Database. مؤرشف من الأصل في 2022-03-08. اطلع عليه بتاريخ 2022-07-05.
  90. مسح العالم. ترجمة: كاميران حوج. أبو ظبي: هيئة أبو ظبي للثقافة والتراث. 2009. ISBN:9789948014058.

وصلات خارجية
  • أيقونة بوابةبوابة أعلام
  • أيقونة بوابةبوابة ألمانيا
  • أيقونة بوابةبوابة الإمبراطورية الرومانية المقدسة
  • أيقونة بوابةبوابة الفضاء
  • أيقونة بوابةبوابة الفيزياء
  • أيقونة بوابةبوابة تاريخ العلوم
  • أيقونة بوابةبوابة رحلات فضائية
  • أيقونة بوابةبوابة رياضيات
  • أيقونة بوابةبوابة علم الفلك
  • أيقونة بوابةبوابة علوم
  • أيقونة بوابةبوابة نجوم
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.