فيزياء الكرة النطاطة
تتعلق فيزياء الكرة النطاطة بالسلوك الجسدي للكرات النطاطة بشكل عام حيث تهتم بدراسة حركة الجسم قبل السقوط وأثناءه وبعد اصطدامه بالأرض لذلك فهي تعتبر مادة دراسية جيدة لشرح مقدمة عن علم الميكانيكا في المرحلتي الثانوية والجامعية لكن يحتاج من يتعمق فيها تطبيق مبادئ الهندسة والميكانيكا على الألعاب الرياضية.

توصف حركة الكرة بشكل كبير حركة القذيفة حيث بتأثر كلاهما بكل من الجاذبية، مقاومة الموائع، تأثير ماغنوس وقانون الطفو لكنها تتميز بتأثرها بمعامل الاستعادة (الذي يمكن أن يتأثر بطبيعة الكرة، طبيعة السطح المؤثر، سرعة التصادم، الدوران، والظروف المحلية مثل درجة الحرارة والضغط). لذلك تضع هيئة إدارة الرياضة الكرة النطاطة (الصورة المحدثة للعبة كرة أمريكا الوسطى) العديد من القيود على تلك المؤثرات لمنع العبث بخصائص الكرات لضمان اللعب النظيف.[1]
القوة المؤثرة أثناء الرحلة وتأثيرها على الحركة

تتشابه حركة الكرة المرتدة مع حركة القذيفة فهي تتعرض للعديد من القوى مثل:[2][3]
- قوى الجاذبية (FG) تؤثر من مركز الجسم إلى أسفل.
- مقاومة المائع (FD) الناتجة من مقاومة الهواء.
- قوة ماغنوس (FM) الناتجة عن دوران الكرة،
- قوة الطفو (FB)
لتحليل حركة الكرة يتم استخدام قانون نيوتن الثاني:
حيث:
الجاذبية

تؤثر قوة الجاذبية على مركز الكرة إلى أسفل طبقا للمعادلة التالية:[4]
حيث
- m: كتلة الكرة
- g: عجلة الجاذبية والتي تتراوح ما بين 9.764 متر/ ثانية تربيع و 9.834 متر/ ثانية تربيع.[5]
يتم اهمال باقي تأثيرات القوى كالسحب وقوى ماغنوس لصغر قيمتهم وبذلك تصبح الكرة معرضه لقوى الجاذبية فقط وهي ما تعرف بالحالة المثالية وتكون معادلة الحركة بالشكل التالي:
حيث
وبشكل أكثر تحديدا، إذا ارتدت الكرة بزاوية θ مع الأرض، فإن الحركة في المحورين x و y والتي تمثل الحركة الأفقية والعمودية على التوالي توصف بالمعادلة التالية:[6]
|
|
|
عند الأخذ في الاعتبار، كلا من:
- H: أقصى ارتفاع
- R: المدى
- T: زمن الرحلة
تكون المعادلة بالشكل التالي:[2][6]
عند التعمق في حركة الكرة يتم الأخذ في الاعتبار قيمة مقاومة الهواء (والتأثيرات ذات الصلة مثل قوى مقاومة الموائع وقوى الرياح) وتأثير ماغنوس وقوى الطفو.
مقاومة الموائع
يمكن أن يكون تدفق الهواء حول الكرة إما صفائحيًا أو مضطربًا استنادًا على عدد رينولدز (Re)، المعرّف على النحو التالي:
حيث:
- ρ: كثافة الهواء
- μ: اللزوجة الديناميكية للهواء
- D: قطر الكرة
- v: سرعة الكرة
كل هذه القيم عند 20 درجة مئوية، ρ = 1.2 kg/m3، ولزوجة 1.8×10−5 باسكال ثانية.[7]
إذا كان رقم رينولدز منخفضًا جدًا أقل من 1، يتم وصف قوى السحب المؤثرة على الكرة من قانون ستوكس:[8]
حيث:
- r: نصف قطر الكرة
- اتجاه الكرة هي اتجاه القوى،
تتراوح قيمه عدد رينولدز لمعظم الكرات الرياضية ما بين 104 و 105 وبذلك لا يتم تطبيق قانون ستوكس وإنما يتم تطبيق المعادلة التالية:[9][10]
حيث:
- Cd: معامل السحب
- A: مساحة المقطع العرضي للكرة
تتسبب قوى السحب في فقدان الكرة للطاقة الميكانيكية أثناء رحلتها والتي تؤدي إلى تقليل نطاق وارتفاع الكرة، في حين تعمل الرياح المتعامدة عن تحولها من مسارها الأصلي. يأخذ لاعبي الألعاب الرياضية مثل الجولف تأثير كلا القوتين.
تأثير ماغنوس

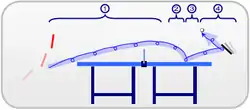
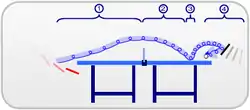
يؤثر دوران الكرة على مسارها من خلال تأثير ماغنوس، وفقا لنظرية كوتا - جوكويسكي التي تصف مجال الغزل مع تدفق الهواء غير المرئي فإن قوة ماغنوس تساوي:[11]
حيث:
- r: نصف قطر الكرة.
- ω: السرعة الزاوية (معدل دوران الكرة).
- ρ: كثافة الهواء.
- v: سرعة الكرة بالنسبة إلى الهواء.
يتم توجيه هذه القوة بشكل عمودي على الحركة وعمودي على محور الدوران. يتم توجيه القوة لأعلى أو لأسفل عن طريق تحديد مركز الدوران. في الواقع لا يتم إهمال قيمة التدفق لتكون المعادلة بالشكل التالي:
حيث:
- ρ: كثافة الهواء.
- CL: معامل الرفع.
- A: مساحة المقطع العرضي للكرة.
- v: سرعة الكرة بالنسبة للهواء.
يعتبر معامل الرفع عامل معقدا يعتمد على العديد من البيانات مثل نسبه rω/v، وعدد رينولدز، وخشونة السطح.[12] في بعض الحالات، يمكن أن يكون معامل الرفع سالبا مما يعني تغير اتجاه قوة ماغنوس أي أن التأثير في الاتجاه المعاكس لما تم افتراضه قبل إجراء الحسابات.[4][13]
في الألعاب الرياضية مثل التنس أو الكرة الطائرة، يمكن للاعب استخدام تأثير ماغنوس للتحكم في مسار الكرة أثناء الرحلة. في لعبة الجولف أيضا، يمكن أن يكون التأثير مسؤولاً عن التقطيع والتركيب التي عادة ما تكون ضارة بالجولف، ولكنها تساعد أيضًا في زيادة مدى القيادة.[14][15] أما في لعبة البيسبول، يستخدم الرماة التأثير لرمي كرات منحنية.[16]
غالبًا ما يكون التلاعب بالكرة غير قانوني، وغالبًا ما يتسبب في حدوث خلافات خصوصا في لعبة الكريكيت مثل الخلاف بين إنجلترا وباكستان في أغسطس 2006.[17] في لعبة البيسبول، يشير المصطلح «تفل الكرة» إلى الطلاء غير القانوني للكرة باستخدام البصق أو مواد أخرى لتغيير الديناميكا الهوائية للكرة.[18]
قوى الطفو
أي جسم مغمور في مائع سواء كان هذا المائع سائل أو غاز يتعرض لقوى الطفو،[19] وفقا لمبدأ أرخميدس، فإن هذه القوة تساوي وزن السائل النازح بواسطة الجسم. في حالة الكرة، تكون قوة الطفو تساوي:
عادة ما تكون قوة الطفو صغيرة مقارنة بقوتي السحب وتأثير ماغنوس، لذلك يتم إهمال قيمتها في أغلب الأحيان. لكن في حالة كرة السلة والحالات المماثلة لها، يمكن أن تصل قوى الطفو إلى حوالي 1.5% من وزن الكرة- نظرا لأنه تأثير الطفو إلى أعلى- مما يؤدي إلى زيادة مدى الكرة وارتفاعها.[19]
الإصطدام
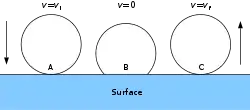
عند اصطدام الكرة بسطح ما يتكون حرارة وصوت، الناتجة من فقدان الكرة جزءا من طاقتها الحركية كما تتحول جزءا من تلك الطاقة إلى طاقة حركة دورانية. أما الجزء المفقود من تلك الطاقة فتعتمد على قيمة الرد ويتم التعبير عنه وفقا للمعادلة التالية:[22][note 1]
حيث:
- vf: السرعة النهائية للكرة
- vi: السرعة الابتدائية للكرة
- uf: السرعة النهائية المؤثرة على السطح
- ui: السرعة الابتدائية المؤثرة على السطح
إذا وقعت كرة على سطح متحرك، يتم تعريف معامل الرد وفقا للمعادلة التالية:[23]
حيث:
- r: نصف القطر
- ω: السرعة الزاوية
- R: نصف قطر الجسم المؤثر (مثل مضرب البيسبول)
- Ω: السرعة الزاوية للجسم المؤثر
- rω: السرعة العرضية لسطح الكرة
- RΩ: السرعة العرضية للسطح المؤثر
تكون تلك المعادلات ذات أهمية عندما تؤثر الكرة على السطح بزاوية مائلة أو عندما يتعلق الأمر بالدوران.
أما في حالة السقوط المستقيم على الأرض بدون دوران، مع تأثير قوة الجاذبية فقط على الكرة، تكون المعادلة بالشكل التالي:[21][24]
حيث:
- K: الطاقة الحركية
- U: طاقة الوضع
- H: أقصى ارتفاع للكرة
- T: زمن رحلة الكرة
يشير الحرفان i و f إلى الحالة الأولية (قبل التصادم) والنهائي (بعد الإرتطام) للكرة. وبالمثل، يمكن ربط فقدان الطاقة بالمعامل الرد بواسطة المعادلة التالية:
يمكن أن يتأثر معامل الرد الخاص بالكرة بعدة أشياء، حيث يتأثر بشكل أساسي:
- طبيعة السطح المؤثر (مثل العشب والخرسانة والشبكات السلكية).[24][25]
- مادة الكرة (مثل الجلود والمطاط والبلاستيك).[21]
- الضغط داخل الكرة (إذا جوفاء).[21]
- مقدار الدوران الناجم عن الكرة عند الاصطدام.[26]
- سرعة التأثير.[20][21][25][27]
يمكن للظروف الخارجية مثل درجة الحرارة تغيير خصائص السطح المؤثر أو الكرة، مما يجعلها إما أكثر مرونة أو أكثر صلابة. وهذا بدوره سيؤثر على معامل الرد.[21] بشكل عام، سوف تتشوه الكرة بشكل أكبر عند السرعات العالية التأثير وبالتالي ستفقد المزيد من طاقتها مما يقلل من معامل الرد.[21][27]
الدوران وزاوية التأثير

عند اصطدام جسم الكرة بالأرض، يتحول جزء من الطاقة الحركية للجسم إلى طاقة حركة دورانية تحدد قيمتها واتجاه دورانها وفقا لزاوية سقوط الكرة وسرعتها الزاوية. في حالة تحرك الكرة أفقيا عند الإصطدام، فسوف تتعرض لقوى احتكاك تؤثر في الاتجاه المعاكس لحركة الكرة. في الشكل المقابل، تتحرك الكرة في اتجاه اليمين وبالتالي يكون اتجاه تأثير قوى الاحتكاك في اليسار. أما في حالة دوران الكرة عند الاصطدام، فسيكون للاحتكاك رد فعل دوراني في الاتجاه المعاكس لدوران الكرة. يظهر في الشكل المقابل، دوران الكرة في اتجاه عقارب الساعة وتتحرك النقطة التي اصطدمت بالأرض نحو اليسار بينما تؤثى القوى الدورانية المعاكسة في اتجاه اليمين. على عكس القوة العمودية وقوة الجاذبية، تؤثر القوى الاحتكاكية على عزم دوران على الكرة وتغيير سرعتها الزاوية (ω).[28][29][30][31] عند سقوط الكرة يمكن أن تنشأ ثلاث حالات وهم:[31][32][33]
- إذا دفعت الكرة للأمام مع دوران سفلي، فإن الاحتكاك السطحي والدوراني يعمل في نفس الاتجاهات. تقل السرعة الزاوية للكرة بعد الاصطدام وكذلك سرعتها الأفقية ويتم دفع الكرة لأعلى وربما تتجاوز ارتفاعها الأصلي بل من الممكن أيضا أن تبدأ الكرة في الدوران في الاتجاه المعاكس أو ترتد حتى إلى الخلف.
- إذا دفعت الكرة للأمام مع دوران علوي، فإن كلا من قوى الاحتكاك السطحي وقوى الدوران سيعملان في اتجاهين متعاكسين. يعتمد ما سيحدث على أين من القوتين ستهيمن.
- إذا كانت الكرة تدور بسرعة أكبر بكثير مما كانت تتحرك، فإن قوى الدوران ستهيمن. تهبط قيمة السرعة الزاوية للكرة بعد الاصطدام، لكن تزداد قيمة السرعة الأفقية. سيتم دفع الكرة للأمام ولكنها لن تتجاوز ارتفاعها الأصلي، وستظل تدور في نفس الاتجاه.
- إذا كانت الكرة تتحرك بسرعة أكبر بكثير مما كانت تدور به، فإن قوى الاحتكاك ستهيمن. يتم زيادة السرعة الزاوية للكرة بعد التصادم، لكن تنخفض سرعتها الأفقية. لن تتجاوز الكرة ارتفاعها الأصلي وستظل تدور في نفس الاتجاه.[31]
إذا كان السطح يميل بمقدار معين θ، فسيتم تدوير المخطط بأكمله بقيمة θ، لكن مع بقاء تأثير قوة الجاذبية إلى أسفل (تشكل زاوية θ مع السطح). عندها يكون للجاذبية عنصر موازٍ للسطح، مما يساهم في الاحتكاك، وبالتالي يساهم في الدوران. في رياضات المضرب مثل تنس الطاولة أو كرة المضرب، يستخدم اللاعبون الماهرون الدوران (بما في ذلك الدوران الجانبي) في تغيير اتجاه الكرة فجأة عند اصطدامها بسطح ما سواء كان ذلك السطح أرض أو مضرب الخصم.
كرات غير كروية

لا يمكن أن يتم التنبؤ بارتداد الكرة ذات الشكل البيضاوي (مثل تلك المستخدمة في كرة القدم الأمريكية أو كرة الرجبي) بنفس القابلية التي يمكن أن نتنبأ بها من ارتداد الكرة الكروية. اعتمادا على محاذاة الكرة عند الاصطدام، يمكن للقوة العمودية أن تتحرك للأمام أو خلف مركز كتلة الكرة، بينما تعتمد قوى الاحتكاك على محاذاة الكرة وكذلك دورانها وسرعة الاصطدام.[34]
كرات مكدسة متعددة
توجد بعض النظريات الشعبية التي تذكر الكرات متعددة التكديس. على سبيل المثال، إذا تم وضع كرة تنس أعلى كرة سلة وتم اسقاطهم في نفس الوقت، فإن كرة التنس سترتد أعلى بكثير إذا كانت وقعت بمفردها.[35][36] كانت النتيجة مفاجئة للبعض لرؤيتهم أنها تخترق قانون حفظ الطاقة.[37] لكن بعد الفحص الدقيق نرى أن كرة السلة لا ترتد عالية بنفس الارتفاع عند وضع كرة التنس فوقها وبذلك نرى أن بعض من طاقتها قد انتقلت إلى كرة التنس.[35]
يتضمن التفسير المعتاد دراسة تأثيرين منفصلين: كرة السلة عند اصطدامها بالأرض ثم كرة السلة واصطدامها مع كرة التنس.[35][36] عند افتراض حدوث تصادم مرن تماما، فإن كرة السلة التي تصطدم بالأرض بسرعة 1 م/ ثانية سترتد بسرعة 1 م/ ثانية. بينما تصطدم كرة التنس بسرعة 1 م/ ثانية وترتد بسرعة 2 م/ ثانية بالنسبة لكرة السلة أو 3 م/ ثانية بالنسبة للأرض. هذا يعني أن الكرة سترتد تقريبا إلى 9 أضعاف ارتفاعها الأصلي.[note 2] في الحياة الواقعية، في التصادمات غير المرنة، ستزيد كرة التنس من سرعتها وتردد بمعامل ارتداد أصغر لكنها ترتد بشكل اسرع وأعلى مما كانت عليه بمفردها.[36]
في حين أن افتراضات التأثيرات المنفصلة غير صالحة في الواقع (تظل الكرات على اتصال وثيق مع بعضها البعض خلال معظم التأثير) إلا أنه غالبا ما يستخدم لفهم الظواهر الأكثر تعقيدًا مثل الانهيار الجوهري للنجوم الفائقة،[36] أو مناورات مقلاع الجاذبية.[35][38]
اللوائح الرياضية
تنظم العديد من هيئات إدارة الألعاب الرياضية قواعد استخدام فيزياء الكرة النطاطة بطرق مختلفة، بعضها مباشر وبعضها غير مباشر. من بين تلك الهيئات:[39][40]
- دوري كرة القدم الأسترالية: والتي تنص على ضغط كرة القدم يجب أن يتراوح ما بين 62 كيلو باسكال و 76 كيلو باسكال.[41]
- الاتحاد الدولي لكرة السلة: والتي تنص على أن يكون الضغط كافي لأن ترتد كرة السلة مسافة ما بين 1200 و 1400 مم (من قمة الكرة) إذا سقطت من مسافة 1800 مم (من قاع الكرة). وبذلك تتراوح قيمة الضغط ما بين 0.727 إلى 0.806.[note 3][42]
- الاتحاد الدولي لكرة القدم: والتي تنص على أن تتراوح قيمة الضغط ما بين 0.6 إلى 1.1 درجة غلاف جوي على مستوى سطح البحر (أي ما بين 61- 111 كيلو باسكال).[43]
- الاتحاد الدولي للكرة الطائرة: والتي تنص على أن تتراوح قيمة ضغط الكرة الطائرة ما بين 0.3- 0.325 كيلو غرام ثقلي/ سم2 (29.4 إلى 31.9 كيلو باسكال) للكرة الطائرة في الصالات وما بين 0.175 كيلو غرام ثقلي/ سم 2 إلى 0.225 كيلو غرام ثقلي/ سم 2 (17.2 إلى 22.1 كيلو باسكال) للكرة الطائرة الشاطئية.[44][45]
- الاتحاد الدولي لكرة المضرب: والتي تنظم ارتفاع كرة التنس عندما تسقط على مختلف أنواع الأسطح سواء كانت ناعمة مستوية أو صلبة ذات كتلة عالية. تسمح المنظمة باستخدام العديد من الكرات لمختلف الأسطح. يسمح بأنواع مختلفة من الكرة لأنواع مختلفة من الأسطح. عندما يتم الإسقاط من ارتفاع 100 بوصة (254 سم)، يجب أن يكون الارتداد من 54 إلى 60 بوصة (137–152 سم) للكرات من النوع 1، من 53 إلى 58 في (135–147 سم) للكرات من النوع 2 والنوع 3، و 48–53 بوصة (122–135 سم) لكرات صاحبة الارتداد الأعلى.[46] يتوافق هذا تقريبًا مع قيمة معامل الرد من 0.735-0.775 (كرة من النوع 1)، من 0.728 إلى 0.762 (من النوع 2 و 3 كرات)، ومن 0.693 إلى 0.728 (من كرات الارتفاع العالي) عندما يتم إسقاطها على سطح الاختبار.[note 3]
- الاتحاد الدولي لتنس الطاولة: تنظم سطح الطاولة بحيث ترتد الطرة حوالي 23 سم عند سقوطها من ارتفاع 30 سم.[47] وهذا يتوافق تقريبا مع قيمة معامل الرد والتي تصل إلى حوالي 0.876 ضد سطح اللعب.[note 3]
- الرابطة الوطنية لكرة السلة (إن بي أي): ينظم ضغط قياس كرة السلة ليكون بين 7.5 و 8.5 رطل (51.7 إلى 58.6 كيلو باسكال).[48]
- الدوري الوطني لكرة القدم الأمريكية: ينظم قياس ضغط كرة القدم الأمريكية بين 12.5 و 13.5 رطل لكل بوصة مربعة (86 إلى 93 كيلو باسكال).[49][50][51]
- أر أند إيه: والذي ينص على أن لا يتجاوز ضغط كرة الغولف 0.83.[52]
انظر أيضا
ملاحظات
المصادر
- Whittington، E. M.، المحرر (2001). The Sport of Life and Death: The Mesoamerican Ballgame. Thames & Hudson. ISBN:0-500-05108-9. مؤرشف من الأصل في 2019-12-17.
- Brancazio، P. J. (1985). "Trajectory of a fly ball". The Physics Teacher. ج. 23 ع. 1: 20. Bibcode:1985PhTea..23...20B. DOI:10.1119/1.2341702.
-
Walker، J. (2014). Fundamentals of Physics (ط. 10th Extended). جون وايلي وأولاده [الفرنسية]. Figure 4-8, p. 70. ISBN:978-1-118-23072-5.
{{استشهاد بكتاب}}: صيانة الاستشهاد: علامات ترقيم زائدة (link) - Bush، J. W. M. (2013). "The aerodynamics of the beautiful game" (PDF). في Clanet، C. (المحرر). Sports Physics. Les Éditions de l'École Polytechnique. ص. 171. hdl:1721.1/87576. ISBN:978-2-7302-1615-9.
- Hirt، C.؛ Claessens، S.؛ Fecher، T.؛ Kuhn، M.؛ Pail، R.؛ Rexer، M. (2013). "New ultrahigh-resolution picture of Earth's gravity field". Geophysical Research Letters. ج. 40 ع. 16: 4279–4283. Bibcode:2013GeoRL..40.4279H. DOI:10.1002/grl.50838.
- Nave، R. "Trajectories". HyperPhysics. مؤرشف من الأصل في 2019-07-18. اطلع عليه بتاريخ 2017-01-27.
- "Dry air properties". The Engineering Toolbox. مؤرشف من الأصل في 2019-04-09. اطلع عليه بتاريخ 2017-02-11.
- Southard، J. (Fall 2006). "Chapter 3: Flow past a sphere II: Stoke's law, the Bernoulli equation, turbulence, boundary layers, flow separation" (PDF). Special Topics: An Introduction to Fluid Motions, Sediment Transport, and Current-generated Sedimentary Structures. معهد ماساتشوستس للتكنولوجيا. ص. 35–82. مؤرشف من الأصل (PDF) في 2017-02-05.
- "Drag of a sphere". ناسا. مؤرشف من الأصل في 2019-05-28.
-
Metha، R. D. (2008). "Sports ball aerodynamics". في Nørstrud، H. (المحرر). Sport Aerodynamics. Springer (publisher). DOI:10.1007/978-3-211-89297-8_12. ISBN:978-3-211-89296-1.
{{استشهاد بكتاب}}: النص "Springer" تم تجاهله (مساعدة) - "Ideal lift of a spinning ball". ناسا. مؤرشف من الأصل في 2018-09-04. اطلع عليه بتاريخ 2017-02-02.
- Nathan، A. M. (2008). "The effect of spin on the flight of a baseball" (PDF). American Journal of Physics. ج. 76 ع. 2: 119. arXiv:physics/0605041. Bibcode:2008AmJPh..76..119N. DOI:10.1119/1.2805242. مؤرشف من الأصل (PDF) في 2019-05-26.
- Kim، J.؛ Park، H.؛ Choi، H.؛ Yoo، J. Y. (2011). "Inverse Magnus effect on a rotating sphere" (PDF). 64th Annual Meeting of the APS Division of Fluid Dynamics. American Physical Society. Bibcode:2011APS..DFD.A7008K.
- "Magnus effect". HumanKinetics.com. مؤرشف من الأصل في 2018-12-28. اطلع عليه بتاريخ 2017-01-27.
- DeForest، C. (1997). "Why are golf balls dimpled?". The Original Usenet Physics FAQ. مؤرشف من الأصل في 2018-10-24. اطلع عليه بتاريخ 2017-01-27.
- Clanet، C. (2015). "Sports ballistics" (PDF). Annual Review of Fluid Mechanics. ج. 47: 455. Bibcode:2015AnRFM..47..455C. DOI:10.1146/annurev-fluid-010313-141255. مؤرشف من الأصل (PDF) في 2017-03-29.
- "Inzamam charged by ICC". الغارديان. 21 أغسطس 2006. مؤرشف من الأصل في 2018-11-18. اطلع عليه بتاريخ 2017-01-28.
- Okrent، D.؛ Wulf، S. (1989). Baseball anecdotes. Oxford University Press. ص. 89. ISBN:978-0-19-504396-9. مؤرشف من الأصل في 2020-01-08.
- Post، S. (2010). Applied and computational fluid mechanics. Jones and Bartlett Publishers. ص. 280–282. ISBN:978-1-934015-47-6. مؤرشف من الأصل في 2019-12-17.
- Cross، R. (1999). "The bounce of a ball" (PDF). American Journal of Physics. ج. 67 ع. 3: 222. Bibcode:1999AmJPh..67..222C. DOI:10.1119/1.19229. مؤرشف من الأصل (PDF) في 2018-12-23.
- Georgallas، A.؛ Landry، G. (2016). "The coefficient of restitution of pressurized balls: A mechanistic model". Canadian Journal of Physics. ج. 94 ع. 1: 42. Bibcode:2016CaJPh..94...42G. DOI:10.1139/cjp-2015-0378. مؤرشف من الأصل في 2017-02-05.
- "Coefficient of restitution". RacquetResearch.com. مؤرشف من الأصل في 2016-11-23. اطلع عليه بتاريخ 2017-01-27.
- Cross، R.؛ Nathan، A. M. (2006). "Scattering of a baseball by a bat". American Journal of Physics. ج. 74 ع. 10: 896–904. arXiv:physics/0605040. Bibcode:2006AmJPh..74..896C. DOI:10.1119/1.2209246.
- Haron، A.؛ Ismail، K. A. (2012). "Coefficient of restitution of sports balls: A normal drop test". IOP Conference Series: Materials Science and Engineering. ج. 36 ع. 1: 012038. Bibcode:2012MS&E...36a2038H. DOI:10.1088/1757-899X/36/1/012038.
- Cross، R. (2000). "The coefficient of restitution for collisions of happy balls, unhappy balls, and tennis balls" (PDF). American Journal of Physics. ج. 68 ع. 11: 1025. Bibcode:2000AmJPh..68.1025C. DOI:10.1119/1.1285945. مؤرشف من الأصل (PDF) في 2018-12-22.
- Cross، R. (2002). "Grip-slip behavior of a bouncing ball" (PDF). American Journal of Physics. ج. 70 ع. 11: 1093. Bibcode:2002AmJPh..70.1093C. DOI:10.1119/1.1507792. مؤرشف من الأصل (PDF) في 2018-12-22.
- Zhang، X.؛ Vu-Quoc، L. (2002). "Modeling the dependence of the coefficient of restitution on the impact velocity in elasto-plastic collisions". International Journal of Impact Engineering. ج. 27 ع. 3: 317–341. DOI:10.1016/S0734-743X(01)00052-5.
- Hesser-Knoll، M. (2014). "Ball spin during bounce". The Physics of Tennis. University of Alaska Fairbanks. مؤرشف من الأصل في 2019-01-02. اطلع عليه بتاريخ 2017-02-01.
- Lindsey، C. (أبريل 2004). "Follow the bouncing ball". Tennis Industry. مؤرشف من الأصل في 2018-11-20. اطلع عليه بتاريخ 2017-02-01.
- Allen، T.؛ Haake، S.؛ Goodwill، S. (2010). "Effect of friction on tennis ball impacts". Proceedings of the Institution of Mechanical Engineers, Part P. ج. 224 ع. 3: 229–236. DOI:10.1243/17543371JSET66.
- Cross، R. (2005). "Bounce of a spinning ball near normal incidence" (PDF). American Journal of Physics. ج. 73 ع. 10: 914–920. Bibcode:2005AmJPh..73..914C. DOI:10.1119/1.2008299. مؤرشف من الأصل (PDF) في 2018-09-21.
- Allen، T. (2012). "The ball's in your court" (PDF). ANSYS Advantage ع. Web exclusive. مؤرشف من الأصل (PDF) في 2017-02-05.
- Jafri، S. M. M. (2004). Modeling of impact dynamics of a tennis ball with a flat surface (PDF) (Thesis). Texas A&M University. hdl:1969.1/2441. مؤرشف من الأصل (PDF) في 2017-09-22.
- Cross، R. (2011). "Bounce of an oval shaped football" (PDF). Sports Technology. ج. 3 ع. 3: 168. DOI:10.1080/19346182.2011.564283. مؤرشف من الأصل (PDF) في 2019-03-24.
- Huebner، J. S.؛ Smith، T. L. (1992). "Multi-ball collisions" (PDF). The Physics Teacher. ج. 30 ع. 1: 46. Bibcode:1992PhTea..30...46H. DOI:10.1119/1.2343467. مؤرشف من الأصل في 2020-01-26.
- Cross، R. (2007). "Vertical bounce of two vertically aligned balls" (PDF). American Journal of Physics. ج. 75 ع. 11: 1009. Bibcode:2007AmJPh..75.1009C. DOI:10.1119/1.2772286. مؤرشف من الأصل (PDF) في 2019-03-22.
- Harter، W. G. (1971). "Velocity amplification in collision experiments involving superballs" (PDF). American Journal of Physics. ج. 39 ع. 6: 656. Bibcode:1971AmJPh..39..656H. DOI:10.1119/1.1986253. مؤرشف من الأصل (PDF) في 2016-11-10.
- Nave، R. "Double ball drop". هايبرفيزيكس. مؤرشف من الأصل في 2019-06-05. اطلع عليه بتاريخ 2017-01-28.
- . Baseball Digest: 67. يوليو 1963.
-
Sowell، T. (2011). "Dead ball vs lively ball". The Thomas Sowell Reader. بيزيك بوكس .
{{استشهاد بكتاب}}: صيانة الاستشهاد: علامات ترقيم زائدة (link) - Laws of Australian Football 2017 (PDF). AFL. 2017. ص. 15. مؤرشف من الأصل (PDF) في 2019-03-05. اطلع عليه بتاريخ 2018-01-19.
- Official Basketball Rules 2014 Basketball Equipment (PDF). الاتحاد الدولي لكرة السلة. 2014. ص. 12. مؤرشف من الأصل (PDF) في 2017-02-15.
-
Laws of the Game: 2014–15 (PDF). الاتحاد الدولي لكرة القدم. 2014. ص. 15. مؤرشف من الأصل (PDF) في 15 فبراير 2017. اطلع عليه بتاريخ أكتوبر 2020.
{{استشهاد بكتاب}}: تحقق من التاريخ في:|تاريخ الوصول=(مساعدة) - Official Volleyball Rules: 2017–2020 (PDF). الاتحاد الدولي للكرة الطائرة. 2016. ص. 16. مؤرشف من الأصل (PDF) في 2019-04-12.
- Official Beach Volleyball Rules: 2017–2020 (PDF). الاتحاد الدولي للكرة الطائرة. 2017. ص. 15. مؤرشف من الأصل (PDF) في 2018-08-27.
-
ITF Approved Tennis Balls, Classified Surfaces & Recognized Courts (PDF). ITF. 2016. ص. 4–5. مؤرشف من الأصل (PDF) في 26 فبراير 2017. اطلع عليه بتاريخ أكتوبر 2020.
{{استشهاد بكتاب}}: تحقق من التاريخ في:|تاريخ الوصول=(مساعدة) - The International Table Tennis Federation Handbook (PDF). ITTF. 2017. ص. 24. مؤرشف من الأصل (PDF) في 2018-04-24.
-
Official Rules of the National Basketball Association: 2013–2014 (PDF). إن بي أي. 2013. ص. 10. مؤرشف من الأصل (PDF) في 20 مارس 2019. اطلع عليه بتاريخ أكتوبر 2020.
{{استشهاد بكتاب}}: تحقق من التاريخ في:|تاريخ الوصول=(مساعدة) - Botelho، G.؛ Castillo، M. (11 مايو 2015). "'Deflategate:' 4-game suspension for Tom Brady". سي إن إن. مؤرشف من الأصل في 2017-05-19. اطلع عليه بتاريخ 2017-01-27.
- Well, Jr.، T. V.؛ Karp، B. S.؛ Reisner، L. L. (2015). Investigative Report Concerning Footballs Used During the AFC Championship Game on January 18, 2015 (PDF). Paul, Weiss, Rifkind, Wharton & Garrison LLP. مؤرشف من الأصل (PDF) في 2019-11-07.
- Official Playing Rules of the National Football League (PDF). الدوري الوطني لكرة القدم الأمريكية. 2016. ص. 3. مؤرشف من الأصل (PDF) في 2017-09-18.
- Rubenstein، L. (11 مايو 2002). "Getting to COR of game, finally". ذا جلوب اند ميل [الإنجليزية]. مؤرشف من الأصل في 2019-12-17. اطلع عليه بتاريخ 2017-01-27.
لمزيد من القراءة
- بريغز عام 1945، «طرق قياس معامل الاسترجاع وتدوير الكرة»- مجلة أبحاث المعهد الوطني للمعايير والتكنولوجيا.
- كروس أر عام 2011، فيزياء البيسبول والكرة اللينة. ردمك: 978-1-4419-8112-7.
- كروس أر يونيو 2014، «فيزياء الارتداد»- جامعة سيدني.
- كروس أر عام 2015، سلوك الكرة النطاطة- تعليم الفيزياء.
- سترونج عام 2004، تأثير الميكانيكا على الألعاب الرياضية- مطبعة جامعة كامبريدج.
وصلات خارجية
- فيزياء الكرة النطاطة- مشاكل في العالم الحقيقي للفيزياء.
- فيزياء الكرات المرنة ومفهوم المرونة.
- دراسة حركة كرتين نطاطتين.
- فيزياء الكرة النطاطة- على اليوتيوب.
- بوابة الفيزياء
- بوابة رياضة
- بوابة طيران
- بوابة علم المواد
- بوابة فنون