فن الفراكتال
الكسيريات أو الفراكتال عرفت باتسامها شكل من أشكال الفن الخوارزمي، وتم إنشاؤها بحساب الجزيئات الكسورية، وتمثل النتائج المحسوبة كصور ثابته و رسوم متحركة ووسائط، وقد تطور الفن الكسوري منذ منتصف الثمانينات واستمر في تطوره، إنه نمط من فنون الحاسوب و الفن الرقمي الذي يشكل جزء من الوسائل الحديثة، فتجمع لإنتاج نوع من الفن التجريدي.[1]


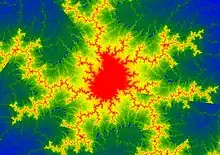
نبذة

بما انها حالة شحيحة لرسم الفن الكسوري (وخاصة في الجزء الغربي من خارطة العالم) عن طريق الرسم على نحو يدوي، وغالبا يكون بإنشاء هذه العملية على نحو غير مباشر ببرمجيات معينة تساعد على ابتكار الكسوريات، ويتم تكرارها وإنتاجها على ثلاث مراحل: إعداد برامترات للبرمجيات، ونظم الدوال المطولة، وتقييم المنتج، وبعض الحالات، يتم استخدام برامج رسم بيانية أخرى لاستمرارية تعديل الصور المنتجة، ويسمى مرحلة مابعد المعالجة، كما يمكن دمج الصور الغير كسورية في الأعمال الفنية، ويمكن اعتبار مجموعة (جوليا) و (ماندلبرو) كبصمة من الفن الكسوري.[2]
افتراضاً إلى أن الفن الكسوري لايمكن بأن يتطور دون أجهزة كمبيوتر؛ بسبب الكم الهائل من العمليات الحسابية التي يوفرها هذا الفن، وتنشأ الكسور بتطبيق دوال متتابعة لحل المعادلات غير الخطية أو المعادلات الحدودية، (والكُسوريات): هي أي من المنحنيات أو أشكال ذات أختلاف متعرج بشكل مهول يكون فيها أجزاء يتم انتقائها على نحو أمثل، مماثلا في تشكيله إلى جزء أكبر أو أصغر، باتضخم أو التقلص إلى نفس الحجم الطبيعي.[3]
أنواعها



كما هناك العديد من الأنماط المختلفة متضمنة الصور الكسيرية، ويمكن تقسيمها على عدة مجموعات:
- أولا: تستمد الكسور من الهندسة القياسية باستخدام تحولات متكررة، تحتوي على رقم مشترك مبدئي تماما كخط ذو استقامة مثل كانتور وندفة فون كوخ)، أو (مثلث سيربنسكى)، أو (the إسفنج مينغر). وأًول أرقام كسرية اخترعت في نهاية نهاية القرن 19 حتى أوائل القرن 20 لتصل إلى هذه الفئة.
- ثانيا: IFS – (دوال المهام المتكررة).
- ثالثا: الجذب
- رابعا: الفليمز الكسورية أو (Fractal Flames).
- خامسا: نظام إل للكُسيريات.
- سادسا: الكُسيريات التي نشأت نتيجة لتكرار تعدد الحدود المعقدة، لعل لكونها من أشهر الكسور.
- سابعا: كسور نيوتن، بما في ذلك كسور نوڤا.
- ثامنا: الكاترنيونية الكسورية ذو فائقة ضغطية.
- تاسعا: الفراكتال يتولد من العمليات الكسرية العشوائية.
- عاشرا: ماندلبرو: نوع من خاصية البعد الكسيري.
التعبير الكسيري: مصطلح يتم استخدامه لتمييز الفن البصري عن الفن الشعبي الذي يحتوي على عناصر كُسيرية كالتشابه الذاتي، علاوة على ذلك فإن أفضل مثال على التعبير عن الكسيريات موجود في أنماط (جاكسون بولوك) المرسومة بواسطة تنقيط ورش الأصباغ، وتم تحليلها وأوضح بأنها تحتوي على البعد الكسوري المنسوب إلى تكنيكه.[4]
تقنياتها

واستخدمت الكسور بجميع الأنماط بشكل أساس للفن الرقمي والرسوم المتحركة، كما أصبحت الرسوم البيانية ذات ألوان عالية الدقة، متوفر في جميع مختبرات البحوث العلمية في منتصف الثمانينات، وأُستحدثت الأشكال العلمية للفن، كما أنها أنطوت على الفن الكسوري، ووضعت بشكل منفصل عن الاتجاه السائد للثقافة، اعتبارا من التفاصيل ثنائية الأبعاد الكسيرية مثل مجموعة ماندلبرو، ووجد الكسيريات تطبيقات فنية متنوعة، مثل: إنشاء الأنسجة وومحاكاة نمو النباتات وإنشاء المناظر الطبيعية.
بين حين وآخر يتم دمج الكسور مع الخوارزميات التطورية، إما من قبل انتقاء عينات جيدة الشكل في مجموعة من التغيرات العشوائية المرتبطة في العمل الفني الكسوري كتصميم Electric Sheep، وعندما يستخدم الأشخاص الفراكتال فليمز (Fractal Flames)، التي تم إصدارها عن طريق الحوسبة الموزعة، ومعدل الفليمز الذي يشاهدونه يؤثر على السيرفر، بتقليل الميزات الغير مهمة، ممايزيد من الرغبة في إنتاج تحفة فنية من صنع شرائح المجتمع. والكثير من الصور الكسورية باهرة بسبب انسجامها الأدراك الحسي، ويتم تحقيقها من خلال الأنماط التي تنشأ من توازن النظام ونظرية الفوضى، وتم وصفها بشكل مماثل في الرسم الصيني والأشجار الصغيرة والصخور.[5]
مشاهد طبيعية
 منظر طبيعي ثلاثي الأبعاد تم إنشاؤه باستخدام Terragen ، باستخدام مجموعة Mandelbrot
منظر طبيعي ثلاثي الأبعاد تم إنشاؤه باستخدام Terragen ، باستخدام مجموعة Mandelbrot جزيرة سارك الحقيقية
جزيرة سارك الحقيقية
وأول صورة كسورية تصبوا بأن تصبح عمل فني يذاع صيعة على غلاف مجلة ساينتفك أمريكان العلمية، بتاريخ أغسطس 1985، حيث أظهرت مشهد طبيعي يتكون من الدوال المحتملة في النطاق الخارجي لمجموعة ماندلبرو، وبأن الدوال المحتملة تزداد في لمحة بصرية بنطاق مجموعة ماندلبرو، فكان من الواجب بأن يترك المنشئ رسم المناظر الطبيعية تجمّ نزولا، لذا استوحت لنا كما لو أن مجموعة ماندلبرو كانت في أعلى هضبة من الجبل بجوانب حادة الانحدار، وتم استخدام نفس التقنية بعد سنة واحدة ببعض الصور في (جمال الكسوريات) من قبل هاينز أوتو بيتغن ومايكل ريختر، ووفروا صيغة لتقدير المسافة من نقطة تقع خارج مجموعة ماندلبرو بصياغة مماثلة لمجموعة جوليا، ومثالا على ذلك، فمن الممكن تكوين المناظر الطبيعية من دالة المسافة بنفس الوحدة التكرارية .
الفنانون
ومن الفنانين المخضرمين في مجال الفنون الكسيرية: ديزموند بول هنري، وحامد ناديري ياقنيه، والموسيقي برونو ديغازيو، واستخدم الفنان البريطاني ويليام لاثام في أعمالة الكسور العكسية وبعض الرسوم البيانية في الحاسوب، واستعمل غريغ سامز تصاميم الكسور في الطوابع البريدية والقمصان والأقمشة، وابتكر الأمريكي فيكي براجو متشيل الفن الكسوري الذي ظهر في المعارض وعلى غلاف المجلات، أما سكوت درايفس قام بإبتكار الفراكتال فليمز، واستقصى كارلوس جينزبيرغ الفن الكسوري وأحالة إلى مفهوم يدعى (Homo Fractals): الذي أسّس فرضية بأن الجسد البشري بحد ذاتة يندرج تحت (Ultimate Fractal)، ميرين باركرز من أصل نيوزيلندي دهت واحتكرت مجال فن الفراكتال، كما دوّن كيري ميتشل بيان عن الفن الفراكتالي مصرحا بأن: الفن الكسوري نوع فرعي من الفن البصري ثنائي الأبعاد ومشابه من نواحٍ عديدة من التصوير الفوتوغرافي، كما أن نوع آخرمن هذا الفن دارت حولة الشكوك بعدم الإفصاح عنها، بحيث تعرض الصور الفراكتالية بتجليها كمبطوعات، مما أدى إلى فنانين الفراكتال بعمل شراكة مع الرسامين، لأن المصورين وفنانين الطباعة، تنشأ بينهم صور فراكتالية على شكل صور إلكترونية، وهذا الشكل التقليدي يتقبلة الفنانون البصريون بشكل أسرع، مماجعلهم يدخلون في عالم الفراكتال للفن الرقمي، وإنتاج الكسوريات من الممكن أن يكون ذو مجهود فني أو mathematical pursuit أو soothing diversion، علاوة على ذلك، فإن الكسيريات تتميز بتصميم أوضح من الأنشطة الرقمية الأخرى بما هي عليه أم لا. وتبعا إلى ماتشيل فإن الفن الفراكتالي لايعتبر فن محوسب، وإنما لايوجد فية أي قاعدة، ولايمكن التنبؤ بها، كما من غير الممكن لأي شخص اتقن جهاز الحاسوب بأن يتقن هذا الفن، وعوضا عن ذلك فإن الفن الكسيري ببساطة هو الذي اخترعة فنانوا الفراكتال.[6]
ومؤخراً تم توظيف الفنان الأمريكي هال تيني لتصميم البيئة في فلم حراس المجرة 2.
المعارض

وتم عرض الفن الفراكتالي بالمعارض الفنية الدولية الكبرى، وكان من أول المعارض للفن الفراكتالي، (Map Art): وأنه معرض متنقل لأعمال الباحثون في جامعة بريمن، كما أن عالما الرياضيات هينز أوتو بيتقن ومايكل م. ريختر رأو بأنهم لايريدوا من العامة بأن يجدوا هذه الصور جميلة فقط، بل أيضاً أن يفهموا الخلفية العلمية للصور.
وفي 1989، أمست الكسوريات جزءاً من موضوع لمعرض فني تحت مسمى (Strange Attractors)، كما(Sign of Chaos) التي في المتحف الحديث للفنون المعاصرة، وكان العرض يتكون من صور فوتوغرافية ومنشآت ومنحوتات صُممت لتوفير خطاب علمي أكثر للاختصاص الذي سُلب اهتمام الشعب من خلال صور حاسوبية ملونة بشكل معقد.[7]
مراجع
- Trivedi, K. (1989). "Hindu Temples: Models of a Fractal Universe". The Visual Computer. 5 (4): 243–258. doi:10.1007/BF02153753. S2CID 29185088.
- Bovill, Carl (1996). Fractal geometry in architecture and design. Boston: Birkhauser. p. 153. ISBN 0-8176-3795-8. Retrieved 28 October 2011.
- Elysia Conner (February 25, 2009). "Meet Reginald Atkins, mathematical artist". CasperJournal.com. Archived from the original on April 20, 2012. Retrieved October 28, 2011.
- Burger, Edward B.; Michael P. Starbird (2005). The heart of mathematics: an invitation to effective thinking. Springer. p. 475. ISBN 1-931914-41-9. Retrieved 30 October 2011.
- Steven R., Holtzman (1995). Digital Mantras: The languages of abstract and virtual worlds. MIT Press. p. 241. ISBN 0-262-58143-4. Retrieved 28 October 2011.
- Penny, Simon (1995). Critical issues in electronic media. State University of New York Press. pp. 81–82. ISBN 0-7914-2317-4. Retrieved 29 October 2011.
- Wang, Hongyu (2005). "Chinese aesthetics, Fractals and the Tao of Curriculum". In Doll, Jr, William E.; Fleener, Jayne; Trueit, Donna; et al. (eds.). Chaos, complexity, curriculum and culture. New York: Peter Lang Publishing. p. 301. ISBN 978-0-8204-6780-1. Retrieved 28 October 2011.
روابط خارجية
- بوابة تقانة المعلومات
- بوابة رياضيات
- بوابة علم الحاسوب
- بوابة فنون
- بوابة فنون مرئية
- بوابة هندسة رياضية
.jpg.webp)