دلالة موضعية
الدلالة الموضعية أو تدوين قيمة المكان أو الترميز الموضعي (بالإنجليزية: Positional notation) هو طريقة لتمثيل أو ترميز الأرقام. يتميز الترميز الموضعي عن الرموز الأخرى (مثل الأرقام الرومانية) باستخدامه نفس الرمز لمرات مختلفة القيمة (على سبيل المثال، «مكان الآحاد»، «مكان العشرات»، «مكان المئات».... وهكذا). وبهذا أصبح الحساب بسيطا إلى حد كبير، مما أدى إلى الانتشار السريع لهذه الطريقة في جميع أنحاء العالم.
مع استخدام النقطة العشرية في النظام العشري، يمكن توسيع هذه الطريقة لتشمل الكسور والأعداد الحقيقية.
نظام الأرقام البابلي، الذي كان أساسه 60، هو أول نظام يستخدم قيمة المكان، وما زال تأثيره موجودا حتى اليوم بالطريقة التي يتم فيها حساب الوقت والزوايا، مثل 60 دقيقة في الساعة، 360 درجة في الدائرة. نظام الأرقام الهندية العربية يستخدم القاعدة 10، وهو النظام الأكثر استخدامًا في العالم اليوم لمعظم العمليات الحسابية. نظام الأرقام الثنائية، يستخدم القاعدة 2، يتم تنفيذه بشكل مباشر في الدوائر الإلكترونية الرقمية ويستخدم من قبل جميع أنظمة الكمبيوتر والإلكترونيات لإجراء الحسابات والتمثيلات.
تاريخيا

يستخدم نظام القاعدة 10 (العشري) حاليا في كل مكان. وقد استخدمت قواعد أخرى في الماضي، وبعضها لا يزال يستخدم حتى اليوم. على سبيل المثال، كان نظام الأرقام البابلية، المعتمد كأول نظام يستخدم دلالة الموضع، يستخدم الأساس 60 ، ولكنه افتقر إلى قيمة حقيقية للعدد 0. تمت الإشارة إلى الصفر بواسطة مسافة بين الأرقام. بحلول سنة 300 قبل الميلاد، تم ترميز رمز الترقيم (اثنين من الأسافين المائلة) لحفظ المكان في نفس النظام. وفي أحد الاكتشافات في كيش (التي يرجع تاريخها إلى حوالي 700 قبل الميلاد) كتب الكاتب Bêl-bân-aplu أصفاره بثلاثة خطافات، بدلاً من الأسافين المائلة.[1] لم يكن العنصر النائب البابلي صفراً حقيقياً لأنه لم يتم استخدامه وحده. كما أنه لم يستخدم في نهاية الرقم. وهكذا بدت الأرقام مثل 2 و 120 (2 × 60)، 3 و 180 (3 × 60)، 4 و 240 (4 × 60) متشابهة، لأن الأعداد الكبيرة كانت تفتقر إلى عنصر نائب في نهايتها. وكان يمكن تمييزها فقط من السياق.
اخترع أرخميدس (ca. 287-212 قبل الميلاد) نظامًا موضعيًا عشريًا في كتابه " Recogner Sand" الذي استند إلى 10 8 [2] وقاد لاحقًا عالم الرياضيات الألماني كارل فريدريك غاوس للتعبير عن ارتياح ما كان يمكن أن يصل إليه العلم في أيامه إذا كان أرخميدس قد أدرك تماما إمكانات اكتشافه البارع.[3]
قبل أن يصبح الترميز الموضعي قياسيًا، تم استخدام أنظمة مضافة بسيطة (تدوين علامة القيمة) مثل الأرقام الرومانية، واستخدم المحاسبون في روما القديمة وأثناء العصور الوسطى المعدادات (أباكوس) أو العدادات الحجرية للقيام بالعمليات الحسابية.[4]
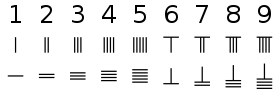
</br> شكل علوي عمودي
</br> شكل أفقي سفلي
تم استخدام قضبان العد ومعظم العدادات (أباكوس) لتمثيل الأعداد في نظام الأرقام الموضعية. مع وجود قضبان العد أو المعداد للقيام بعمليات حسابية، يمكن بسهولة كتابة قيم البدء والقيمة المتوسطة والنهائية للحساب من خلال نظام إضافة بسيط في كل موضع أو عمود. لم يتطلب هذا النهج أي حفظ للجداول (كما هو الحال في التدوين الموضعي) ويمكن أن يعطي نتائج عملية بسرعة. على مدى أربعة قرون (من القرن الثالث عشر إلى السادس عشر) كان هناك خلاف قوي بين أولئك الذين كانوا يؤمنون بتبني النظام الموضعي في كتابة الأرقام وأولئك الذين أرادوا البقاء مع نظام المضاف-مع-المعداد. على الرغم من أن الآلات الحاسبة الإلكترونية قد حلت بشكل كبير محل المعداد، إلا أن الأخير لا يزال يستخدم في اليابان ودول آسيوية أخرى لتعليم الأطفال.
بعد الثورة الفرنسية (1789-1799)، روجت الحكومة الفرنسية الجديدة لتمديد النظام العشري.[5] بعض هذه الجهود المؤيدة للنظام العشري - مثل الوقت العشري والتقويم العشري - لم تنجح.ابينما جهود تحويل العملات decimalisation والنظام المتري من الأوزان والمقاييس فقد انتشرت على نطاق واسع من فرنسا إلى العالم كله تقريبا.
تاريخ الكسور الموضعية
يلاحظ لينارت بيرغرين (J. Lennart Berggren) أن الكسور العشرية الموضعية استخدمت لأول مرة من قبل عالم الرياضيات العربي أبو الحسن الإقليدسي في القرن العاشر.[6] استخدم عالم الرياضيات اليهودي إيمانويل بونفيس الكسور العشرية في حوالي عام 1350، لكنه لم يطور أي تدوين لتمثيلهم.[7] ادعى عالم الرياضيات الفارسي جمشيد الكاشي أنه اكتشف الكسور العشرية بنفسه في القرن الخامس عشر.[6] قدم الخوارزمي الكسور إلى البلدان الإسلامية في أوائل القرن التاسع.[8] هذا الشكل من الكسر بصورة البسط في الأعلى والمقام في الأسفل بدون خط أفقي كان يستخدمه أبو الحسن الإقليدسي أيضا في القرن العاشر من القرن الماضي، وواستخدمه جمشيد الكاشي في القرن الخامس عشر في مؤلفه «مفتاح الحساب».[8][9]

يُعدُ سيمون ستيفين في القرن السادس عشر رائد العلامة العشرية الأوروبية الحديثة.[10]
مسائل متعلقة بذلك
كانت الحجة الرئيسية ضد النظام الموضعي هي قابليته للتزوير بسهولة عن طريق وضع رقم في بداية أو نهاية العدد، وبالتالي تغيير (على سبيل المثال) 100 إلى 5100 بإضافة القم 5 إلى اليسار، أو 100 إلى 1000 بإضافة الرقم 0 إلى اليمين. ولمنع التزوير تتطلب الشيكات الحديثة كتابة العدد بالحروف، بالإضافة إلى العدد العشري نفسه. وللسبب نفسه، يستخدم الصينيون أيضًا الأرقام باللغات الطبيعية، على سبيل المثال 100 مكتوبة على أنها 壹佰 ، والتي لا يمكن أبدًا تزويرها بـ 壹仟 (1000) أو 伍仟 壹佰 (5100).
الرياضيات
قاعدة نظام الأرقام
في نظم العد الرياضية، يكون الأساس هو عادة عدد الأرقام الفريدة بما في ذلك الصفر، التي يستخدمها نظام الأرقام الموضعية لتمثيل الأعداد. على سبيل المثال، النظام العشري يكون أساسه هو 10، لأنه يستخدم 10 أرقام 10 من 0 إلى 9. فبعد الرقم "9" لن يكون الرقم التالي رمزًا مختلفًا، بل هو "1" متبوعًا بـ "0" أي "10" ويليه "11" وهكذا. وفي النظام الثنائي، يكون الأساس هو 2، لأنه بعد الرقم "1" نستخدم الرقم "10" ثم "11" ويليه "100" وهكذا.
عادة ما يكون أعلى رمز لنظام الأرقام الموضعية هو القيمة الأقل من قيمة أساس هذا النظام الرقمي. تختلف أنظمة الأرقام الموضعية القياسية عن بعضها البعض فقط في «الأساس» الذي تستخدمه.
«الأساس» هو عدد صحيح أكبر من 1 (أو أقل من -1). ونادرا ما يستخدم "أساس سالب لأنه في النظام ذو أساس سالب، يمكن تمثيل الأرقام بالعديد من التمثيلات المختلفة.
(في بعض أنظمة الأرقام الموضعية غير القياسية، فإن تعريف الأساس أو الأرقام المسموح بها يختلف عن ما سبق.))
في الترميز الموضعي للأساس 10 (النظام العشري)، هناك 10 أرقام عشرية والرقم
- .
في نظام الأساس 16 (النظام السداسي عشري)، هناك 16 رقمًا سداسيًا عشريًا (0–9 و A – F) والرقم
(حيث B هي رمز يمثل الرقم 11)
بشكل عام، في نظام الأساس b ، يكون هناك b من الأرقام والعدد
- (لاحظ أن تمثل أرقام)
الرموز
عند وصف «الأساس» في الترقيم الرياضي، يتم استخدام الحرف b عمومًا كرمز (اختصارا لكلمة base)، لذلك، بالنسبة للنظام الثنائي، يكون الأساس b=2. هناك طريقة أخرى شائعة للتعبير عن الأساس وذلك بكتابته على هيئة علامة عشرية (سفلية) بعد الرقم الذي يتم تمثيله (يتم استخدام هذا الترميز في هذه المقالة). فمثلا 1111011 2 يعني أن الرقم 1111011 هو رقم أساس 2، وهو يساوي 123 10 (وفق النظام العشري)، وكذلك يساوي 173 8 (بنظام العد الثماني).
يمكن أيضًا الإشارة إلى الأساس b بعبارة «أساس-b». إذن الأرقام الثنائية هي «أساس-2»؛ الأرقام الثمانية هي «أساس-8»؛ الأرقام العشرية هي «أساس-10» وهكذا.
عند استخدام أساس b نستخدم مجموعة من الأرقام {0، 1... b-2، b-1} وتسمى مجموعة الأرقام القياسية. وبالتالي تحتوي الأرقام الثنائية على أرقام {0، 1} ؛ في حين تحتوي الأرقام العشرية على أرقام {0, 1, 2, ..., 8, 9}; وهكذا. ولذلك فالأرقام التالية بها أخطاء: لأنها تستخدم أرقاما أكبر من الأساس 52 2 ، 2 2 ، 1A 9 .
الأس
تعمل أنظمة الأرقام الموضعية باستخدام الأس لرقم الأساس. فقيمة الرقم هي الرقم المضروب في قيمة مكانه. وقيمة المكان هي رقم الأساس الذي يتم رفعه إلى الأس n ، حيث n هو عدد الأرقام الأخرى بين رقم معين ونقطة الجذر. إذا كان رقم معين على الجانب الأيسر من نقطة الجذر (أي أن قيمته عبارة عن عدد صحيح)، تكون n موجبة أو صفرية؛ إذا كان الرقم على الجانب الأيمن من نقطة الجذر (أي أن قيمته عبارة عن كسور)، يكون n سالبا.
وكمثال على الاستخدام، فإن الرقم 465 يتم تمثيله في الأساس b (والتي يجب أن تكون على الأقل في الأساس 7 لأن الرقم الأعلى فيها هو 6) يساوي:
إذا كان الرقم 465 في الأساس 10، فسوف يساوي:
(46510 = 46510)
إذا كان الرقم موجودًا في الأساس 7، فسوف يساوي:
(4657 = 24310)
الرقم 10b دائما يساوي b لأي أساس b، وذلك لأن 10b = 1×b1 + 0×b0. على سبيل المثال:, 102 = 2; 103 = 3; 1016 = 1610. بينما إذا كان الرقم من خانة واحدة فقيمته هي نفسها لا تتغير.
يمكن إثبات هذا المفهوم باستخدام رسم بياني. كائن واحد يمثل وحدة واحدة. عندما يكون عدد الكائنات مساويًا أو أكبر من الأساس b ، يتم إنشاء مجموعة من الكائنات بعدد b من الكائنات. عندما يتجاوز عدد هذه المجموعات b، ثم يتم إنشاء مجموعة من هذه المجموعات من الكائنات مع b من المجموعات وb من الكائنات؛ وهكذا. وبالتالي فإن العدد نفسه في أنظمة ذات أساسات مختلفة سيكون له قيم مختلفة:
العدد 241 في نظام الأساس 5: به مجموعتين من 52 (25) و 4 مجموعات من 5 ومجموعة واحدة من 1 ooooo ooooo ooooo ooooo ooooo ooooo ooooo ooooo + + o ooooo ooooo ooooo ooooo ooooo ooooo
العدد 241 في نظام الأساس 8: به مجموعتين من 82 (64) و 4 مجموعات من 8 ومجموعة واحدة من 1 oooooooo oooooooo oooooooo oooooooo oooooooo oooooooo oooooooo oooooooo oooooooo oooooooo + + o oooooooo oooooooo oooooooo oooooooo oooooooo oooooooo oooooooo oooooooo oooooooo oooooooo
يمكن زيادة الترميز من خلال السماح بعلامة السالب. وهذا يسمح بتمثيل الأرقام السالبة. بالنسبة لأساس معين، فإن كل تمثيل يتوافق مع رقم حقيقي واحد بالضبط، وكل رقم حقيقي له تمثيل واحد على الأقل. تمثل الأرقام الكسرية باستخدام البسط والمقام وبينهما خط أفقي، أو ربما بدورة أرقام متكررة بشكل لا نهائي. فمثلا الرقم (1/3) يمكن تمثيله على الصورة (0.3333333).
الأعداد والأرقام
الرقم (digit) هو ما يستخدم كموضع في تدوين قيمة المكان، والعدد (numeral) هو واحد أو أكثر من الأرقام. الأرقام الأكثر شيوعًا اليوم هي الأرقام العشرية "0" و "1" و "2" و "3" و "4" و "5" و "6" و "7" و "8" و "9".
العدد غير الصفري الذي به أكثر من رقم واحد يُمثل عددا مختلفا وفق نظم العد ذات الأساسات المختلفة، ولكن بصفة عامة، فإن الأرقام تعني نفس الشيء.[11] فالعدد 23 8 في النظام الثماني يحتوي على رقمين، "2" و "3"، ويساوي 19 في النظام العشري، بينما العدد 23 5 يساوي 13 في النظام العشري. وهنا يتضح أهمية كتابة أساس النظام. فلو تخيلنا العدد "23" غير معروف الأساس، فمن المحتمل أن يكون "23" للأساس-4 وبالتالي يساوي 11، أو للأساس-60 وبالتالي يساوي 123. أي أن الرقم "23" يمكن قراءته على أنه "2" من الأساس و "3".
نقطة الجذر (فاصلة الكسر)
يمكن توسيع استخدام الموضع إلى الأس السالب للأساس b . في هذه الحالة، تُستخدم النقطة "radix"، ويُرمز لها "."، كفاصل للمواقع ذات الأس الموجب عن تلك ذات الأس السالب.
تستخدم الأعداد غير الصحيحة أماكن على يمين نقطة الجذر . لكل موضع خلف هذه النقطة (وبالتالي بعد رقم الآحاد)، يتناقص الأس n للقيمة b n بمقدار 1 . على سبيل المثال، العدد 2.35 يساوي:
الإشارة
إذا كان الأساس وكافة الأرقام أرقاما «غير سالبة» فلا يمكن التعبير عن الأعداد السالبة. وللتغلب على هذا، نستخدم علامة ناقص، هنا (-).
تطبيقات
انظر أيضًا
- قائمة أنظمة الأعداد
- نظام العد
- نظام العد الهندي العربي
المصادر
- O'Connor، John؛ Robertson، Edmund (ديسمبر 2000). "Babylonian Numerals". مؤرشف من الأصل في 2019-07-23. اطلع عليه بتاريخ 2010-08-21.
{{استشهاد ويب}}: صيانة الاستشهاد: postscript (link) - Kadvany، John (ديسمبر 2007). "Positional Value and Linguistic Recursion". Journal of Indian Philosophy.
- Knuth، Donald (1997). The art of Computer Programming. Addison-Wesley. ج. 2. ص. 195–213. ISBN:0-201-89684-2.
- Ifrah، George (2000). The Universal History of Numbers: From Prehistory to the Invention of the Computer. Wiley. ISBN:0-471-37568-3. مؤرشف من الأصل في 2022-10-06.
- Kroeber، Alfred (1976) [1925]. Handbook of the Indians of California. Courier Dover Publications. ص. 176. ISBN:9780486233680. مؤرشف من الأصل في 2019-03-13.
المراجع
- كابلان ، روبرت. (2000). لا شيء ما هو: تاريخ طبيعي من الصفر . أكسفورد: مطبعة جامعة أكسفورد.
- الأرقام اليونانية نسخة محفوظة 11 أغسطس 2017 على موقع واي باك مشين.
- Menninger، Karl : Zahlwort und Ziffer. Eine Kulturgeschichte der Zahl ، Vandenhoeck und Ruprecht، 3rd. الطبعه ، 1979 ،
- إفراح ، صفحة 187
- LF Menabrea. ترجمه آدا أوغوستا ، كونتيسة لوفليس. "رسم من المحرك التحليلي من اختراع تشارلز باباج" . 1842. نسخة محفوظة 16 يناير 2019 على موقع واي باك مشين.
- Berggren، J. Lennart (2007). "Mathematics in Medieval Islam". The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. ص. 518. ISBN:978-0-691-11485-9.
- Gandz، S .: اختراع الكسور العشرية وتطبيق الحساب التوسعي بواسطة إيمانويل بونفيلز من تاراسكون (حوالي 1350) ، إيزيس 25 (1936) ، 16–45.
- لام لاي يونغ ، "تطوير الحساب الهندوسي العربي والحساب الصيني التقليدي" ، العلوم الصينية ، 1996 p38 ، تدوين كورت فوغل
- لام لاي يونغ ، "تكوين صيني ، إعادة كتابة تاريخ نظامنا الرقمي" ، أرشيف تاريخ العلوم الدقيقة 38: 101-108.
- B. L. van der Waerden (1985). A History of Algebra. From Khwarizmi to Emmy Noether. Berlin: Springer-Verlag. مؤرشف من الأصل في 2022-07-28.
- سوف يحتفظ الرقم بمعناه في قواعد الأعداد الأخرى ، بشكل عام ، لأن قاعدة العدد الأكبر ستكون عادة امتدادًا للقاعدة الأقل في أي منظمة منظمة. في العلوم الرياضية ، هناك نظام واحد فقط لترقيم الموضعية لكل قاعدة تحت 10 ، وهذا يمتد مع اختلافات قليلة ، إن لم تكن ذات دلالة ، على اختيار الأرقام الأبجدية لتلك القواعد فوق 10.
- بوابة التاريخ
- بوابة رياضيات