دالة تربيعية
في علم الجبر، يشير مصطلح الدالة التربيعيّة أو كثير الحدود التربيعيّ أو كثير الحدود من الدرجة الثانية أو ببساطة التربيعيّ إلى دالة كثير حدود بمتغير واحد أو أكثر، أعلى درجة فيه هي 2. على سبيل المثال، تحتوي الدالة التربيعيّة ذات المتغيرات الثلاثة x و y و z بشكل حصريّ على الحدود x2 و y2 و z2 و xy و xz و yz و x و y و z وثابت:
| دالة تربيعية | |
|---|---|
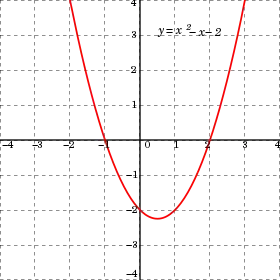 A كثير حدود تربيعيّ ذو جذرين حقيقيَّين (نقاط تقاطع الرسم البياني مع المحور x) وبالتالي لا يوجد جذور عُقَدِيّة. بعض كثيرات الحدود التربيعيّة تمتلك قيماً صُغرى فوق المحور x، وفي هذه الحالة لا يوجد للدالة جذور حقيقيّة ولكن يوجد لها جذرين عُقَدِيَّين. A كثير حدود تربيعيّ ذو جذرين حقيقيَّين (نقاط تقاطع الرسم البياني مع المحور x) وبالتالي لا يوجد جذور عُقَدِيّة. بعض كثيرات الحدود التربيعيّة تمتلك قيماً صُغرى فوق المحور x، وفي هذه الحالة لا يوجد للدالة جذور حقيقيّة ولكن يوجد لها جذرين عُقَدِيَّين. | |
| تدوين | |
| مشتق الدالة | |
| مشتق عكسي (تكامل) |
|
| الميزات الأساسية | |
| زوجية أم فردية؟ | زوجية، إذا كان |
| مجال الدالة | |
| المجال المقابل |
|
| قيم محددة | |
| نهاية الدالة عند +∞ | إذا كان
|
| نهاية الدالة عند -∞ | إذا كان
|
| جذور الدالة | |
| نقاط حرجة | |
| ملاحظات | |
بالإضافة إلى أحد المعاملات a أو b أو c أو d أو e أو f للحدود ذات الدرجة الثانية، ويجب أن يكون أحدها على الأقل لا يساوي الصفر. يكون للدالة التربيعية أحادية المتغير، يكون لها الشكل الآتي[1]
في حالة المتغير الواحد، يكون الرسم البياني بشكل قطع مكافئ يكون محور تناظره موازٍ للمحور y كما هو مُوضح في الشكل إلى اليسار. أيضاً تُدعى الدالة التربيعيّة فيما لو ساوَت الصفر المعادلة التربيعيّة. وتكون حلول هذه المعادلة أحاديّة المتغير جُذُور الدالة التربيعيّة أما في حالة الدالة ثنائية المتغيِّرات x و y، يكون للدالة الشكل الآتي
و يكون في هذه الحالة a أو b أو c على الأقل لا تساوي الصفر، وإن مُعادلة هذه الدالة، أي عندما تساوي هذه الدالة صفراً، فإن المعادلة ستعطي قطعاً مخروطيَّاً (دائرة أو قطع ناقص أو قطع مكافئ أو قطع زائد). عموماً، يمكن أن يكون هناك عدد كبير من المتغيرات، وفي هذه الحالة تُدعى السطوح الناتجة بالسطوح من الدرجة الثانية أو السطوح التربيعيّة، ولكن يجب أن تكون أعلى درجة هي الدرجة الثانية، كـ x2, xy, yz إلخ.
اشتقاق الاسم
يُطلَق على الدالة التربيعيّة اسم (بالإنجليزية: Quadratic function) باللغة الإنجليزيّة، وتُشتقُّ من الكلمة اللاتينيّة quadrātum والتي تعني «مُرَبَّع». كما يُطلَق اسم مُربَّع أيضاً في الجبر على الرمز x2 وذلك بسبب تشكُّل منطقة بشكل مربَّع بجانب X.
المصطلح
المعاملات
تكون عادةً معاملات كثيرات الحدود أرقام حقيقية أو عقديّة، ولكن في الواقع، يمكن تعريف كثير الحدود بأي حلقة.
الدرجة
عند استخدام مصطلح «كثير حدود من الدرجة الثانية»، يقصد الكتاب أحياناً «أن لكثير الحدود الدرجة 2 تماماً»، وأحياناً «أن لكثير الحدود الدرجة 2 على الأكثر». وإذا كانت الدرجة أقل من 2، قد يُدعى كثير الحدود حينها «حالة تدهور». وغالباً يتحدد المعنى المقصود من السياق.
أحياناً تُستخدم كلمة «المرتبة» بمعنى «درجة»، مثلاً كثير حدود من المرتبة الثانية.
المتغيرات
يمكن أن يشتمل كثير الحدود التربيعيّ على متغيّر (متحوِّل) مفرد X (حالة المتغيّر الأحادي) أو عدة متغيرات كـ X و Y و Z (حالة متعددة المتغيِّرات).
حالة متغير واحد
قد يكتب أي كثير حدود تربيعيّ بمتغيّر واحد على الشكل الآتي
حيث x هو المتغيِّر، و aو b و c تُمثِّل المعاملات. وفي الجبر الأولي، غالباً ما تنشأ هكذا كثيرات حدود في شكل معادلة من الدرجة الثانية وتُدعى حلول هذه المعادلة بجذور كثير الحدود من الدرجة الثانية (التربيعيّ)، وقد يكون من الممكن إيجادها من خلال تحليل كثير الحدود إلى عوامله الأوليّة أو إكمال المربع أو من خلال رسم بياني للدالة أو من خلال طريقة نيوتن أو من خلال استخدام الصيغة التربيعية. لكل كثير حدود تربيعيّ دالة تربيعيّة مرافقة يكون تمثيلها البيانيّ قطعاً مكافئاً.
حالة متغيران
قد يُكتب أي كثير حدود تربيعيّ بمتغيرين على الشكل الآتي
حيث x و y متغيِّرات، بينما a و b و c و d و e و f معاملات عدديّة. تُعتبر متحولات كهذه أساساً لدراسة لـلقطوع المخروطيّة، التي تتظاهر بتساوي التعبير عن الدالة f (x, y) إلى الصفر. وبشكل مشابه، فإن كثيرات الحدود بثلاثة متغيرات أو أكثر تتطابق مع السطوح التربيعيّة والسطوح الفائقة. في الجبر الخطيّ، يمكن تعميم فكرة كثيرات الحدود التربيعيّة (من الدرجة الثانية) على فكرة الشكل التربيعيّ على الفضاء المتجهيّ.
أشكال الدالة التربيعيّة ذات المتغير الواحد
يمكن التعبير عن الدالة التربيعيّة وحيدة المتغير بثلاثة صيغ:[2]
- يُدعى الشكل المعياريّ
- يُدعى الشَّكل المُفَكَّك (المُحلَّل إلى عوامل)، حيث r1 وr2 جذور للدالة التربيعيّة وحلول للمعادلة التربيعيّة (من الدرجة الثانية) الموافقة لهذه الدالة.
- يُدعى الشكل المُتَّجِهيّ h وkوx وy هي إحداثيّات المتجه على التوالي.
للمعامل a القيمة ذاتها في الأشكال الثلاثة. وللتحويل من الشكل المعياري إلى الشكل المُفكَّك (المحلل إلى عوامله)، يحتاج المرء فقط للصيغة التربيعيّة لتحديد الجذرين r1 وr2. وللتحويل من الشكل المعياريّ إلى الشكل المتجهيّ، يحتاج المرء إلى القيام بعملية تُدعى إكمال المربع. وللتحويل من الشكل المُفكَّك (المحلل إلى عوامله) إلى الشكل المعياريّ، يحتاج المرء إلى مضاعفة و/أو توسيعها و/أو نشر العوامل.
رسم الدالة التربيعية وحيدة المتغير



بغض النظر عن صيغة الدالة التربيعيّة، فإن الرسم البيانيّ للدالة التربيعيّة وحيدة المتغيّر يُمثِّلُ قطعاً مكافئاً (كما هو واضح في الشكل إلى اليسار). وبالمقابل، فإن الرسم البياني للمعادلة التربيعيّة ثنائية المتغيرات .
- إذا كان a > 0، فإن فتحة (تقعُّر) المنحني تتجه لأعلى
- إذا كان a < 0، فإن فتحة (تقعُّر) المنحني تتجه لأسفل
يتحكَّم المعامل a بدرجة انحناء الرسم البيانيّ، كلَّما ازدادت قيمة a يصبح انحناء الرسم البيانيّ أكثر حدَّةً أي أكثر انغلاقاً. يتحكَّم المعاملان b وa معاً بموقع محور التناظر للقطع المكافئ (أيضاً إحداثيات x لذروة المنحني) والذي
بينما يتحكَّم المعامل c بنقطة تقاطع القطع المكافئ مع المحور y.
الذروة
تقابل ذروة القطع المكافئ نقطة انحراف القطع المكافئ، لذا قد تُدعى بنقطة الانحراف. وإذا كانت الدالة التربيعيّة في الشكل المتجهيّ، فإن إحداثيات الذروة هي (h, k). ويمكن باستخدام طريقة إكمال المربع، تحويل الشكل المعياريّ
إلى الشكل
لذا تكون ذروة القطع المكافئ (h, k) في الشكل المعياريّ
وإذا كانت الدالة التربيعيّة بالشكل المتفكك (المتحلِّل إلى عوامله)
فإن متوسط الجذرين
هو إحداثية x الموافقة لذروة القطع، وتكون إحداثيات الذروة (h, k)
كما أن الذروة أيضاً هي أكبر نقطة إذا كانت a < 0 أو أصغر نقطة إذا كانت a > 0 وإن الخط العمدي التالي
والذي يم من الذروة هو أيضاً محور تناظر القطع المكافئ.
القيمتين الكبرى والصغرى
باستخدام التفاضل والتكامل، يمكن الحصول على نقظة الذروة والتمي تمثِّل القيمة الكبرى أو الصغرى للدالة، وذلك عبر إيجاد جذور الاشتقاق:
x هي جذر f '(x) إذا كانت f '(x) = 0 وبالتالي
وبالتعويض في الدالة نجد
وبالتالي يمكن التعبير عن إحداثيات الذروة (h, k) بالصيغة
جذور الدالة وحيدة المتغير

- الجذور وy-مشار إليها بـالأحمر
- الذروة ومحور التناظر مُشارٌ إليهما بـالأزرق
- البؤرة والمِحرَق مُشار إليهما بـالوردي

الجذور
إن جذور (أو أصفار) الدالة التربيعيّة أحاديّة المتغيّر r1 وr2
هي قيم x التي تجعل f(x) = 0. وعندما تكون المعاملات a وb وc أعداد حقيقية أو أعداد عُقديّة تكون حينها الجذور
الحد الأعلى لحد الجذور
لا يمكن للقيمة المطلقة لجذور كثير حدود تربيعيّ (من الدرجة الثانية) أن تكون أكبر من حيث النسبة الذهبيّة وهي [4]
الجذر التربيعي لدالة تربيعية وحيدة المتغير
يؤدي الجذر التربيعيّ لدالة تربيعية أحادية المتغيّر إلى واحدة من أربع مقاطع مخروطيّة غالباً على نحو أكيد إلى قطع ناقص أو إلى قطع زائد. إذا كانت فإن المعادلة تصف قطعاً زائداً، كما يمكن رؤيته من خلال تربيع الجانبين. تتحدَّد اتجاهات محاور القطع الزائد بواسطة ترتيب النقطة الأدنى (قيمتها على محور y) من القطع المكافئ المقابل . إذا كان ترتيبها سالباً، فإن المحور الرئيسي للقطع الزائد (المار من ذروته) أفقيّ، بينما إذا كان ترتيبها موجباً سيكون المحور الرئيسي للقطع الزائد عموديَّاً. إذا كانت فإن المعادلة تصف إما دائرة أو قطعاً ناقصاً أو لا تصف شيئاً على الإطلاق. إذا كان ترتيب النقطة الأكبر من القطع المكافئ المقابل موجباً فإن الجذر التربيعيّ يصف قطعاً ناقصاً، ولكن إذا كان الترتيب سالباً فإنه يصف موضع فارغ من النقاط.
التكرار
لتكرار دالة يتم تطبيق الدالة مراراً وتكراراً، باستخدام المخرجات من أحد التكرارات كمُدخل في التكرار التالي. لا يمكن للمرء أن يستنتج دائماً الشكل التحليليّ لـ والذي يعني أن nth تكراراً لِـ.(يمكن أن يمتد الخط العلوي حتى أرقام سالبة، مما يشير إلى تكرار عكس إذا كان العكس موجوداً) ولكن هناك حالات يكون التعبير فيها بالشكل المغلق. على سبيل المثال، للمعادلة التكرارايّة الآتية
وعندما يكون
حيث
- and
و بالاستقراء نجد
يمكن الحصول عليه، حيث يمكن حسابه بسهولة كـ
أخيراً لدينا
وهو الحل. يمكن حل المتتالية اللوجستية
بالمعلمة 2<r و r<4 في حالات محددة، إحداها الحالة الفوضويّة وإحداها ليست. في الحالات الفوضويّة r=4 الحل هو
حيث تُعطى معلمة الحالة البدئية بواسطة . ولقيمة عقلانية لِـ، بعد عدد منتهي من التكرارات متتالية إلى سلسلة دوريّة. ولكن تقريباً جميع غير منطقيّة، ومن أجل منطقية لا تُكرِّر نفسها أبداً، وهي غير دوريّة وتعتمد على الحالة البدئية، لذا يُقال أنها فوضويّة.
حل المتتالية اللوجيستية عندما تكون r=2
الحل:
من أجل . وإذا لأي قيمة من ما عدا النقطة المثبتة غير المستقرة 0، المصطلح يسعى إلى 0 كما تسعى n إلى اللانهاية، لذا فإن تسعى إلى النقطة الثابتة المستقرة.
دالة تربيعية ثنائية المتغيرات
يشير مصطلح الدالة التربيعيّة ثنائية المتغيرات إلى كثير حدود من الدرجة الثانية من الشكل
حيث A و B و C و D و E معاملات ثابتة و F حدٌ ثابت. تصف الدالة التربيعية ثنائية المتغيرات باعتبارها دالة سطحاً تربيعيَّاً (من الدرجة الثانية). وإن الإعداد يُعادل الصفر ويصف تقاطع السطح مع المستوى ، وهو موضع من النقاط مُعادل للقطع الناقص.
النقاط الصغرى والكبرى
إذا كانت فإن الدالة ليس لها قيم صغرى أو كبرى، ورسمها البيانيّ سطح مكافئ زائدي إذا كانت فإن للدالة قيمة صغرى إذا كان A>0 وقيمة كبرى إذا كان A<0، ويكون الرسم البياني للدالة سطح مكافئ إهليلجيّ. في هذه الحالة تقع القيم الصغرى أو الكبرى عند حيث:
و إذا كانت و لا يكون للدالة قيم صغرى أو كبرى، ويكون الرسم البيانيّ بشكل أسطوانة مكافئة. إذا كانت و فإن الدالة تحقق قيم صغرى وكبرى عند حد أدنى إذا كانت A>0 وأعلى إذا كانت A<0، ويكون رسمها البياني بشكل أسطوانة مكافئة
انظر أيضًا
مراجع
- "Quadratic Equation -- from Wolfram MathWorld". مؤرشف من الأصل في 2019-03-26. اطلع عليه بتاريخ 2013-01-06.
- Hughes-Hallett، Deborah؛ Connally، Eric؛ McCallum، William G. (2007)، College Algebra، John Wiley & Sons Inc.، ص. 205، ISBN:9780471271758، مؤرشف من الأصل في 2022-10-16, "three+different+forms+for+a+quadratic+expression+are" Search result
- "Complex Roots Made Visible – Math Fun Facts". مؤرشف من الأصل في 2019-06-01. اطلع عليه بتاريخ 2016-10-01.
- Lord, Nick, "Golden bounds for the roots of quadratic equations", Mathematical Gazette 91, November 2007, 549.
- بوابة تحليل رياضي
- بوابة رياضيات