خوارزمية لي
خوارزمية لي معروفة أيضًا بخوازمية حلّ المتاهة.[1] هي واحدة من خوارزميات استطلاع المسار و لقيت رواجا تطبيقيا في توجيه أشرطة الربط على لوحات الدوائر الإلكترونية. إنّها تاريخيا أقدم طريقة أدرجت في أنظمة التصميم الألي لاللّوحة المطبوعة و الدارات المتكاملة .
الخوارزمية
يتم تعريف المتاهة على أنها شبكة من النقاط. تبحث هذه الخوارزمية على أفضل مسار بين نقطة البداية S ونقطة الوصول المتصلة A، وتتجنب النقاط التي تم تعريفها على أنها عوائق. الخوارزمية تتكوّن من أربع إجراءات متتالية و هي :
التهيئة
- انتقل إلى نقطة البداية S ، اسندها علامة 0
- 0 ← i
الانتشار
- كرر
- لجميع النقاط التي تحمل علامة i
- لجميع النقاط المجاورة النقطة التي تحمل علامة i
- إذا كانت النقاط المجاورة بدون علامة و ليست عائق
- اسند النقاط المجاورة علامة i + 1
- نهاية إذا
- إذا كانت النقاط المجاورة بدون علامة و ليست عائق
- نهاية لجميع
- لجميع النقاط المجاورة النقطة التي تحمل علامة i
- نهاية لجميع
- إذا لم توجد نقطة لها علامة i + 1
- نهاية الخوارزمية : المسار غير ممكن
- نهاية إذا
- i + 1 → i
- لجميع النقاط التي تحمل علامة i
- حتى نقطة بعلامة i = الوصول A
استعاد الطريق
- علامة نقطة الوصول i = A
- طالما i≠1
- انتقل إلى النقطة المجاورة التي تحمل علامة 1 - i
- أضف هذه النقطة إلى المسار
- i - 1 → i
- نهاية طالما
التنظيف
- ألغي جميع العلامات الحالية
مثال تنفيد
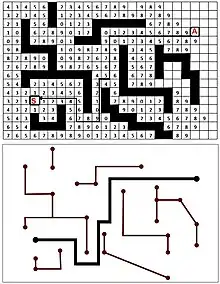
الصورة هنا على اليسار توضح كيف تعمل خوارزمية لي على شبكة 24 × 16. التطبيق يتمثل في توجيه الروابط في لوحة إلكترونية مطبوعة. الاتساق كيف تلتقي العلامات في جميع النقاط قبل العوائق وبعدها يثير الإعجاب. المسار المستعاد ليس فريدًا ، لكن الخوارزمية تضمن أنّ جميع المسارات الممكن استعادها متساوية المسافة.
مراجع
- LEE, Chin Yang. An algorithm for path connections and its applications. IRE transactions on electronic computers, 1961, no 3, p. 346-365.
- بوابة خوارزميات