ثماني سطوح
في الهندسة الرياضية، المُجسَم الثُماني أو ثماني الأوجه أو ثماني السطوح (بالإنجليزية: Octahedron)، جسم ثلاثي الأبعاد مُتعدد الأسطح له ثمانية أوجه، واثنا عشر ضلع، وستة رؤوس.[1][2] يُسمى نظامياً عندما تكون أوجهه مثلثات متساوية الأضلاع. ويُعتبر كهرمين رباعي الأوجه مُزدوجين. يمثل الهيكل الهندسي التركيبي لعدد من الأجسام بالطبيعة.
| منتظم ثماني الأوجه | |
|---|---|
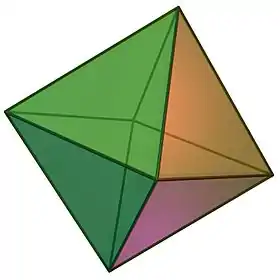 (اضغط هنا لتدوير المُجسَم) | |
| النوع | مجسم أفلاطوني |
| مميزة أويلر | F = 8, E = 12 V = 6 (χ = 2) |
| الوجوه من الجوانب | 8{3} |
| ترميز كونواي | O aT |
| رمز شليفلي | {3,4} |
| r{3,3} or | |
| تكوين الوجه | V4.4.4 |
| رمز ويتهوف | 4 | 2 3 |
| مخطط كوكستير-دينكين | |
| التماثل | Oh, BC3, [4,3], (*432) |
| مجموعة التناوب | O, [4,3]+, (432) |
| المراجع | U05, سكوت ماكدونالد كوكستر17, W2 |
| الخصائص | منتظم، محدب |
| زاوية زوجية | 109.47122° = arccos(−13) |
 3.3.3.3 (شكل رأسي ) |
 مكعب (متعدد الأوجه المزدوج) |
 شبكة (متعدد أوجه) | |
منتظم ثماني الأوجه
الأبعاد
إذا كان طول ضلع ثماني الأوجه هو a، فإن نصف قطر المجال المقيد (الذي يلمس الثماني الأفقي في جميع القمم) هو:
ونصف قطر المجال المدرج (المماس لكل من الوجوه الثماني) هو:
في حين أن منتصف القطر الذي يمس وسط كل ضلع، هو:
الإسقاطات المتعامدة
| التمركز | الضلع | الوجه الطبيعي |
قمة الرأس | الوجه |
|---|---|---|---|---|
| الصورة |  |
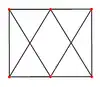 |
 |
 |
| التماثل الإسقاطي |
[2] | [2] | [4] | [6] |
التبليط الكروي
يُمكن أن يتم تمثيل ثماني الأوجه على شكل تبليط كروي، بحيث يكون إسقاط السطح عبر إسقاط المجسم. هذا الاسقاط يُحافظ على الزوايا ولكن ليس الأطوال والمراكز. وتكون خطوط مستقيمة على المجال كأقواس دائرية على متن السطح.
 |
 |
| إسقاط عمودي | إسقاط متواز |
|---|
المساحة والحجم
مساحة السطح A والحجم V لثماني الأوجه والضلع هو a. ويكون الحساب كالتالي:
وبالتالي فإن حجم أربع مرات من رباعي سطوح يساوي طول الضلع، في حين يساوي مساحة السطح مرتين (لأن لدينا 8 بدلاً من 4 مثلثات).
ثماني الأوجه في العالم المادي
ثماني الأوجه في الطبيعة

ثماني الأوجه في الفن والثقافة
- لعبة ثعبان روبيك [الإنجليزية] تشكل أحدها ثماني الأوجه.
- فيلم ترون (1982) أخذ أحد الشخصيات (Bit) شكل ثماني الأوجه.
مراجع
- "معلومات عن ثماني الأوجه على موقع mathworld.wolfram.com". mathworld.wolfram.com. مؤرشف من الأصل في 2019-06-08.
- "معلومات عن ثماني الأوجه على موقع jstor.org". jstor.org. مؤرشف من الأصل في 2019-05-26.
- بوابة رياضيات
- بوابة هندسة رياضية