فضاء ثلاثي الأبعاد

تنقسم المجسمات إلى قسمين هما:

أ - المجسمات المنتظمة الحجم: وهي التي يمكن إيجاد حجمها عن طريق الحساب العادي.

ب - المجسمات غير المنتظمة الحجم: وهي التي لا يمكن إيجاد حجمها بالطرق التقليدية.

مكعب

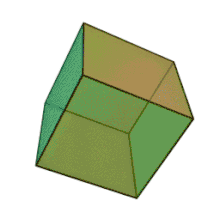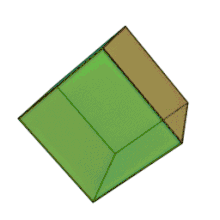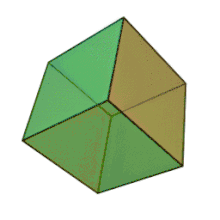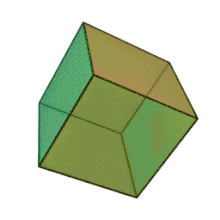
يتكون المكعب من:

• 6 أوجه متطابقة على شكل مربعات كلها
• 12 حرفا متساوية وهو الواصل ما بين مربعين على المكعب
• 8 رؤوس وهي تجمع أطراف ثلاثة حروف

حجم الكعب = طول الحرف × نفسه × نفسه

يتكون متوازي المستطيلات من:

• 6 أوجه كلها مستطيلات أحيانا وبإمكان تواجد وجهين على شكل مربع
• 12 حافة
• 8 رؤوس

وإذا كان لمتوازي المستطيلات وجهين على شكل مربع فلا ينتظم حروفه حجم متوازى المستطيلات = الطول × العرض × الارتفاع.

الكرة هي مجسم ليس له أي أضلاع أو حروف أو رؤوس.

الهرم هو مجسم جوانبه مثلثات، وقاعدته إما ثلاثية أو رباعية أو خماسية وما يشبه ذلك.

المخروط هو مجسم ينتج من توصيل جميع نقاط منحنى مغلق بنقطة لا تنتمي إليه، ويسمى المنحنى الخط الدليلي والنقطة بـرأس المخروط ويسمى كل مستقيم يوصلة بين الخط الدليلي والرأس بـراسم المخروط

الكرة من المجسمات

للمنشور نوعان:

• القائم: هو الموشور حيث تتعامد الأحرف الجانبية مع أضلع القاعدتين.
• المائل: هو كل ما يخالف المنشور القائم.

تندرج معظم الأشياء التي يتعامل معها الفرد بالمجسمات المنتظمة الحجم مثال (الحجرة، الكتاب، الحاويات، كرة القدم، أهرامات الجيزة).