توزيع ماكسويل-بولتزمان
توزيع ماكسويل-بولتزمان هو توزيع احتمالي يستخدم في تطبيقات عديدة في الفيزياء والكيمياء ، وفي الديناميكا الإحصائية .حيث تعتمد درجة حرارة نظام فيزيائي كبير على حركة مكوناته من الذرات أو الجزيئات و تتميز الجزيئات بسرعات مختلفة .[1][2][3] وتختلف سرعة الجزيء من وقت لآخر بسبب اصطدامه بالجزيئات الأخرى. ويكون عدد الجزيئات التي تكون لها سرعة معينة ثابتاً عند وصول النظام إلى حالة الاتزان الحراري . ويمكننا تعيين فئة من تلك الجزيئات ذات السرعة الواحدة بحساب توزيع ماكسويل للسرعات عند درجة حرارة معلومة للنظام. ويـُعرف هذا التوزيع بتوزيع ماكسويل وبولتزمان .
تطبيقات عملية لتوزيع ماكسويل-بولتزمان
يمثل توزيع ماكسويل-بولتزمان أساس نظرية حركة الغازات ( كينتيكا الغازات kinetic gas theory ) التي تصف خواص الغازات بما فيها ضغط الغاز وانتشاره . ويعطي توزيع ماكسويل-بولتزمان توزيع سرعات الجزيئات في الغاز، كما يعطينا أيضا توزيع عزوم الجزيئات وطاقة حركتها، وكل من تلك الخواص له دالة خاصة به ولكنها تنتمي لبعضها البعض.
ويمكن الحصول على توزيع ماكسويل-بولتزمان بوساطة الميكانيكا الإحصائية (إحصاء ماكسويل ) ، وهي تُعطي السرعة الأكثر احتمالاً في نظام كبير من الجزيئات التي لا تتفاعل مع بعضها، ولا يحدث بينها سوى الاصطدامات المرنة، مع افتراض عدم وجود تأثيرات كمومية بينها.
وتوجد حالات كثيرة لا تنطبق تلك الشروط عليها، مثل التصادم الأيونات في الطبقة الأيونية للأرض [أيونوسفير). وتصادم البلازما في الفضاء الخارجي. والصدمات المتسببة للتأين. والاصطدامات التي تصدر إشعاعاً وعلى الأخص تصادم الإلكترونات . فتطبيق توزيع ماكسويل-بولتزمان علي تلك الحالات يوصلنا إلى نتائج خاطئة لا تتفق مع الطبيعة .
وهناك مجال آخر لا يصح فيه تطبيق توزيع ماكسويل-بولتزمان . ذلك عندما يكون طول موجة الإشعاع الحراري للغاز مقاربا لمتوسط المسافات بين الجزيئات .في هذه الحالة فلن تستطيع النظرية تعيين تأثيرات نظرية الكم . وكذلك لا يأخذ هذا التوزيع في الاعتبار تأثيرات النظرية النسبية التي لا تسمح بأن يكون للجزيء سرعة أعلى من سرعة الضوء . فكانت دراسة وصياغة هذا التوزيع في النصف الثاني من القرن التاسع عشر، أي نحو 60 عاما قبل ظهور نظرية الكم والنظرية الذرية .
تعيين توزيع ماكسويل-بولتزمان
أخذ التوزيع الأصلي الذي صاغه ماكسويل في الاعتبار أن حركة الجزيئات تتماثل في الاتجاهات الثلاثة، إلا أن الصياغة التي اتبعها بولتزمان ألغت ذلك الشرط بفضل اعتماده على نظرية حركة الغازات Kinetic Theory . ويمكن في وقتنا هذا استنباط توزيع ماكسويل-بولتزمان من توزيع بولتزمان للطاقة :
حيث:
Ni عدد الجزيئات في الحالة i
T درجة الحرارة المطلقة
i الحالة أو مستوي الطاقة
Ei طاقة المستوي i
gi عدد المستويات التحتية للطاقة Ei
N العدد الكلي للجزيئات في النظام
(مع ملاحظة أنه في بعض الأحوال لا تهتم بذكر g عدد المستويات التحتية في Ei)
في تلك الحالة يعرف i حالة معينة من الطاقة بدون اعتبار مستوياتها التحتية . وبما أن السرعة تتحكم في الطاقة، يمكننا استعمال المعادلة أعلاه لاستنباط العلاقة بين درجة الحرارة وسرعة الجزيئات في الغاز. ويسمى المقام في تلك المعادلة دالة التوزيع طبقا لتعريفات الميكانيكا الإحصائية statistical mechanics.
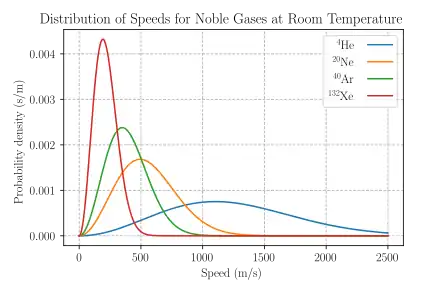
يعطي هذا الرسم منحني ماكسويل-بولتزمان لعدد من الغازات الخاملة واحتمال تواجد الذرات في السرعات المختلفة . ويلاحظ أن الهيليوم له أعلي متوسط للسرعة (نحو1150 متر/ثانية)نظرا لخفته، بينما الإكسينون وهو أثقلهم فمتوسط سرعة ذراته تبلغ نحو 200 متر في الثانية . ويحدث ذلك طبقا للعلاقة بين طاقة الحركة والكتلة التي تقول :
طاقة الحركة: E = 1/2. mv2
حيث:
- m الكتلة،
- و v السرعة .
مراجع
- * Maxwell, J.C. (1860 B): Illustrations of the dynamical theory of gases. Part II. On the process of diffusion of two or more kinds of moving particles among one another. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 4th Ser., vol.20, pp.21-37. نسخة محفوظة 20 أغسطس 2017 على موقع واي باك مشين.
- Gyenis، Balazs (2017). "Maxwell and the normal distribution: A colored story of probability, independence, and tendency towards equilibrium". Studies in History and Philosophy of Modern Physics. ج. 57: 53–65. arXiv:1702.01411. Bibcode:2017SHPMP..57...53G. DOI:10.1016/j.shpsb.2017.01.001.
- Laurendeau، Normand M. (2005). Statistical thermodynamics: fundamentals and applications. Cambridge University Press. ص. 434. ISBN:0-521-84635-8. مؤرشف من الأصل في 2016-06-24.
- بوابة الفيزياء