توزيع الرتبة والحجم

إن مصطلح توزيع الرتبة والحجم أو قاعدة الرتبة والحجم (أو قانون الرتبة والحجم) يصف الانتظام الملحوظ في العديد من الظواهر بما في ذلك توزيع أحجام المدن حول العالم وأحجام الأعمال التجارية وأحجام الجزيئات (الرمال على سبيل المثال) وأطوال الأنهار وتواتر استخدام الكلمات والثروة التي يمتلكها الأفراد وغير ذلك. وجميع هذه المعلومات ناتجة عن ملاحظة العالم الحقيقي الذي يتّبع قوانين القوة مثل تلك المعروفة باسم قانون زيبف أو توزيع يول أو توزيع باريتو. إذا قام شخص ما بترتيب حجم السكان في بلد معينة أو في العالم بأكمله ثم قام بحساب اللوغاريتم الطبيعي لرتبة وعدد السكان بالمدينة، فسوف يوضح الرسم البياني نمطًا ملحوظًا من اللوغاريتم الخطي. وهذا هو توزيع الرتبة والحجم.[1]

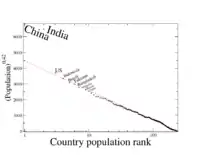
في حالة سكان المدينة، سوف يتميز التوزيع الناتج في أي دولة أو منطقة أو في العالم بوجود المدن الأكبر حجمًا مع تناقص المدن الأخرى في الحجم تبعًا لذلك، حيث يكون ذلك في البداية بمعدل سريع ثم يصبح أقل سرعة شيئًا فشيئًا. وينتج عن ذلك قلة عدد المدن الكبيرة وعدد أكبر بكثير من المدن الأصغر حجمًا. على سبيل المثال، المدينة التي في الرتبة 3 يكون عدد سكانها 1/3 عدد سكان أكبر مدينة في الدولة، والمدينة التي في الرتبة الرابعة يكون عدد سكانها 1/4 عدد سكان أكبر مدينة، وهكذا.

عند ترتيب أي عامل لوغاريتمي خطي، فإن هذه الرتب تتبع أعداد لوكاس، والتي تتكون من الأعداد المضافة بالتسلسل التالي 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, إلخ. ويشبه ذلك تسلسل فيبوناتشي الأكثر شهرة، حيث إن كل عدد يساوي تقريبًا 1.618 (النسبة الذهبية) من العدد الذي يسبقه. على سبيل المثال، في التسلسل المذكور أعلاه، العدد 4 يزيد بمقدار 1.618³ أو 4.236 (أي تقريبًا 4); والعدد الرابع في التسلسل، 7, يزيد تقريبًا بمقدار 1.618⁴ أو 6.854 (أي تقريبًا 7); والعدد الثامن في التسلسل، 47, يزيد تقريبًا بمقدار 1.618⁸ أو 46.979 (أي تقريبًا 47). ومع ازدياد القيم تتقارب الأرقام. وفي بعض الأوقات يستخدم الحلزون متساوي الزوايا في وضع تصور لهذه التسلسلات.

تزعم إحدى الدراسات [2] أن قاعدة الرتبة والحجم «مجدية» لأنها «ظل» أو إجراء حدث بالصدفة لظاهرة طبيعية. وبالتالي فإن القيمة الحقيقية للرتبة والحجم ليست إجراءً رياضيًا دقيقًا (حيث إن الصيغ الأخرى لقانون القوة أكثر دقة، خاصة للرتب التي تقل عن 10) لكنها بالأحرى إجراء مفيد أو «بحكم الخبرة» لرصد قوانين القوة. عند التقديم مع بيانات الترتيب، هل يكون المتغير بالرتبة الثالثة يساوي تقريبًا 1/3 قيمة الأعلى رتبة في الترتيب؟ أو على العكس من ذلك، هل المتغير الأعلى رتبة يساوي تقريبًا عشر مرات قدر المتغير في الرتبة العاشرة؟ إن كان هذا صحيحًا، يمكن أن تساعد قاعدة الرتبة والحجم في اكتشاف علاقة أخرى مع قانون القوة.

وعلى الرغم من أن قانون زيبف يعمل بشكل جيد في الكثير من الحالات لكنه لا يناسب المدن الكبيرة في الكثير من الدول. وجدت دراسة في عام 2002, أن قانون زيبف رفضته 53 دولة من بين 73 دولة، وهذا العدد أكبر من المتوقع على أساس الفرص العشوائية.[3] كما وجدت الدراسة أن اختلافات أُس باريتو يمكن شرحها بصورة أفضل من خلال المتغيرات السياسية وليس من خلال المتغيرات الاقتصادية والجغرافية مثل وكلاء اقتصاديات الحجم أو تكاليف النقل.[4] وبينت دراسة أجريت في عام 2004 أن قانون زيبف لا يعمل بصورة جيدة على المدن الخمس الكبرى في ستة دول.[5] وفي الدول الأكثر ثراءً، كان التوزيع أكثر سطحية بدلاً من أن يكون متوقعًا. على سبيل المثال، في الولايات المتحدة الأمريكية، على الرغم من أن كبرى مدنها، مدينة نيويورك، بها أكثر من ضعف عدد السكان في لوس أنجلوس، التي في المرتبة الثانية وتقع المدينتان في مناطق حضرية وهما الأكبر بالدولة، كما أن عدد السكان بهما متقارب. بالنسبة لعدد السكان في المناطق الحضرية، يبلغ عدد سكان مدينة نيويورك فقط 1.4 مرة قدر عدد سكان لوس أنجلوس. وفي دول أخرى يمكن أن تسيطر المدن الكبرى أكثر مما هو متوقع. على سبيل المثال، في الكونغو الديمقراطية، فإن عاصمتها كينشاسا أكبر بما يزيد عن ثماني مرات عن المدينة التي في المرتبة الثانية، لوبومباشي. عند التفكير في التوزيع الكامل للمدن، بما في ذلك المدن الصغيرة، لا تسري قاعدة المرتبة والحجم عليها. بل يكون التوزيع باللوغاريتم الطبيعي. وهذا ناتج عن قانون جيبارت حول النمو النسبي.