توزيع أسي
في نظرية الاحتمالات والإحصاء، التوزيع الأسي[1] توزيع احتمالي مستمر اشتق اسمه من الدالة الأسية.[2][3] ويستعمل هذا التوزيع في تخمين الفترات الزمنية بين وقوع الأحداث في سيرورة بواسون.
دالة الكثافة الاحتمالية 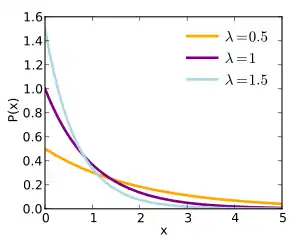 | |
دالة التوزيع التراكمي 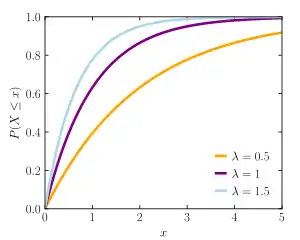 | |
| المؤشرات | λ> 0 |
| الدعم | x ∈ [0, ∞) |
| د۔ك۔ح۔ | λ e−λx |
| د۔ت۔ت | 1 − e−λx |
| المتوسط الحسابي | λ−1 |
| الوسيط الحسابي | λ−1 ln 2 |
| المنوال | 0 |
| التباين | λ−2 |
| التجانف | 2 |
| التفرطح | 6 |
| الاعتلاج | 1 − ln(λ) |
| د۔م۔ع | |
| الدالة المميزة | |
| معلومات فيشر | {{{معلومات فيشر}}} |
الاستخدام
عادة ما يستخدم التوزيع الأسي في مسائل متعلقة بقياس الزمن. من ذلك مدة خدمة شباك البريد، مدة المكالمة هاتفية، مدة تفريغ باخرة الشحن، مدة تصليح آلة، مدة انتظار زبون قبل الحصول على الخدمة. في العلوم الدقيقة يستخدم التوزيع الأسي لتمثيل مدة حياة الذرات المشعة قبل أن تتفكك، حيث يعبر الوسيط عن اللحظة التي يبقى فيها نصف المجتمع الأصلي.
كقاعدة عامة يستخدم التوزيع الأسي لتمثيل مدة حياة ظاهرة ما إذا كان لها متوسط ثابت 1/λ وكانت هذه الظاهرة لا تخضع للتقادم أي أن مدة حياة الظاهرة بعد لحظة ما T لا تتبع اللحظة T؛ أي لا تتأثر بالمدة التي دامتها الظاهرة من قبل. مثلا قد نستبعد استخدام التوزيع الأسي لتمثيل مدة حياة آلة عاملة قبل تعطلها لأن احتمال تعطلها في لحظة ليس مستقلا عن المدة التي عملتها الآلة من قبل، كذلك الأمر بالنسبة لمدة حياة الإنسان.
عمليا، نتحقق من دقة تمثيل التوزيع الأسي أو أي توزيع آخر لظاهرة ما من خلال تقنيات اختبارات الفروض، وبالتحديد اختبار التجانس والتعديل.
للتوزيع الأسي علاقة بتوزيع بواسون، فإذا كان وقوع أحداث ما يتبع هذا التوزيع، فإن المدة بين وقوع حدثين تتبع التوزيع الأسي؛ كمثال على ذلك، إذا كان وصول الزبائن إلى مركز خدمة ما يتبع التوزيع بواسون فإن المدة الزمنية بين وصول زبون «أ» والزبون الموالي تتبع التوزيع الأسي. تتبين هذه العلاقة عند استنتاج صيغة القانون الأسي.
الخواص
دالة الكثافة
يقال أن لمتغير لعشوائي ما أنه يتبع التوزيع الأسي إذا كانت دالة كثافته تعطى بالشكل التالي:
أو يمكن صياغتها باستعمال دالة الخطوة (H(x.
حيث λ > 0 هو متثابت التوزيع.
دالة التوزيع
دالة التوزيع التراكمي لمتغير عشوائي يتبع التوزيع الأسي تعطى بالشكل التالي:
ويمكن صياغتها كذلك باستعمال دالة الخطوة.
مراجع
- معجم البيانات والذكاء الاصطناعي (PDF) (بالعربية والإنجليزية)، الهيئة السعودية للبيانات والذكاء الاصطناعي، 2022، ص. 68، QID:Q111421033
- "معلومات عن توزيع أسي على موقع britannica.com". britannica.com. مؤرشف من الأصل في 2015-09-15.
- "معلومات عن توزيع أسي على موقع babelnet.org". babelnet.org. مؤرشف من الأصل في 2019-12-15.
- بوابة رياضيات
- بوابة إحصاء