تمثيل O الكبرى
في الرياضيات، يستعمل تمثيل O الكبرى أو رمز O الكبرى[1] (بالإنجليزية: Big O notation) من أجل وصف تقارب وتباعد الدوال عن بعضها البعض حينما يقترب المدخل إلى قيمة معينة أو حينما يؤول إلى ما لا نهاية. بشكل عام توجد عدة رموز كل منها له مفهومه الخاص. نشط استخدام هذا الرمز في تحليل سرعة الخوارزميات وذلك لأن حساب عدد العمليات التي تنفذها خوارزمية ما قد يكون مستحيلاً في بعض الأحيان مع وجود كثير من الأمور التي تؤثر على عدد العمليات. لذا فإن إعطاء تقريب لعدد العمليات التي تقوم بها الخوارزمية أكثر راحةً لنا والرمز O الكبير يتيح هذا الامر بسهولة.
تعريف
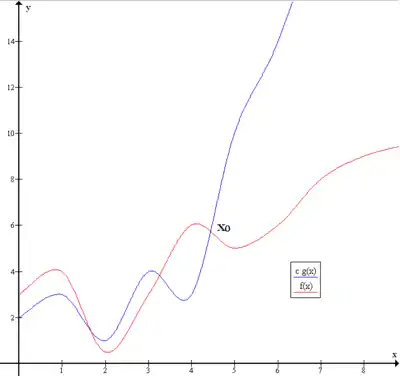
- رمز O كبير: نقول أَنَّ أو إذا كان هنالك ثابت بحيث انه يوجد ولكل يحدث التالي: أي انه إذا تخيلنا رسم الدالتين f و- g حينها نرى ان الدالة f اعلى من الدالة g ابتداء من مكان معين.
على غرار رمز O الكبير يمكن تعريف الرموز التالية:
- رمز Ω : نقول أَنَّ أو إذا كان هنالك ثابت بحيث انه يوجد ولكل يحدث التالي: أي انه إذا تخيلنا رسم الدالتين f و- g حينها نرى ان الدالة f تحت الدالة g ابتداء من مكان معين.
- رمز Θ : نقول أَنَّ أو إذا كان هنالك ثابت بحيث انه يوجد ولكل يحدث التالي: أي انه إذا وأيضا أي انَّ الرسم البياني للدالة g محصور بين وبين .
تحليل الخوارزميات
عند تحليل خوارزمية ما، نريد حساب عدد الحسابات أو سرعة الخوارزمية أو تعقيدها الحسابي، ونستطيع كتابة التعقيد الحسابي اما عن طريق معادلة عودية واما بطريقة مباشرة، في كلا الحالتين نرمز للتعقيد ب- عندما n هو طول المُدخل للخوارزمية، مثال لخوارزمية هي خوارزمية البحث الخطي من المفهوم ضمنا ان عدد حساباتها هو: وذلك لانها تقارن كل عدد في القائمة مرة واحدة مع العدد المُدخل وبما ان طول القائمة هو فرضا n عندها عدد حسابات الخوارزمية هو (قيمة المقارنة الواحدة) وفيمة المقارنة الواحدة تعتمد على نموذج الحساب (computational model) لذا قد يكون من الصعب اعطاء تقريب لهذه القيمة لذا فانه من المفيد ان نفترض ان قيمة كل مقارنة هو عدد ثابت من الحسابات أي انه: يوجد ثابت c بحيث ان كل مقارنة عدد حساباتها اقل من c ، لذا فاننا نحصل على وحسب تعريف رمز O الكبير نحصل على انه .
خواص رمز O كبير والرموز الأخرى
اهمال الثوابت والدوال ذات الدرجة الصغيرة
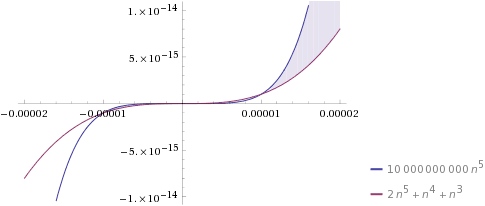
بما ان رمز O الكبير يفترض وجود ثابت c بحيث انه يُحقق امر مُعين (حسب التعريف) لذا فانه يمكن اهمال الثوابت، مثال يمكن اهمال العدد 2 المضروب ب- وكذلك يمكن اهمال وذلك لانه إذا اخذنا ثابت كبير كفاية يمكن حينها ان نهمل الثوابت واحادية الحدود التي اسها صغير وكذلك المعاملات (انظر إلى الصورة) لذا فانه، وبشكل عام إذا كان تعقيد الخوارزمية متعدد الحدود فاذا كان الاس الأكبر هو k حينها: .
خاصية التعدي
وكذلك حينئذ يتحقق
وكذلك حينئذ يتحقق
وكذلك حينئذ يتحقق
خاصية الانعكاسية
خاصية التماثل
إذا وفقط إذا
جدول دوال
| ترميز | تعقيد | مثال لخوارزمية |
|---|---|---|
| ثابت | مقارنة عددين | |
| لوغاريثمي | بحث ثنائي | |
| لوغاريثمي-خطي | تصنيف اعداد | |
| لوغاريثمي-متعدد | فحص الاولية اي باعطائنا عدد افحص إذا ما هو عدد اولي. | |
| خطي | بحث خطي | |
| رباعي | ضرب عددين | |
| حدودي | ضرب مصفوفتين | |
| أسي | تلوين مخطط بثلاثة الوان | |
| عاملي | حل مسـالة البائع المتجول |
انظر أيضا
مراجع
- معجم البيانات والذكاء الاصطناعي (PDF) (بالعربية والإنجليزية)، الهيئة السعودية للبيانات والذكاء الاصطناعي، 2022، ص. 47، QID:Q111421033
- بوابة تحليل رياضي
- بوابة رياضيات
- بوابة علم الحاسوب