تعاكس

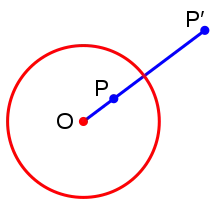
التعاكس هو تحويل هندسي يعكِسُ كلَّ نُقطةٍ على المُستوى حول دائرةٍ ثابتة. يُعرّف انعكاسُ النقطة المُختلفة عن المركز حول الدائرة على أنه نُقطةٌ تقع على الشّعاع تُحقّق العلاقة: . هُناك اختلاف حول صورة المركز ، هناك من يُعرِّفُه على أن صورة هي نفسها، لكن في الغالب فإنَّه يُعرّف على أنه نقطة في اللانهاية. إنّ التعاكسَ الذي ينقلُ النقطةَ إلى صورتها أيضاً ينقل الصورة إلى الأصل ؛ وبهذا تكون دالة التحويل الهندسي الخاصة بالتعاكس دالةً ارتداديَّة، أي بعبارةٍ أخرى: الأصل يؤدي إلى الصورة والصورة تؤدي إلى الأصل.[1][2][3]

النقطة هي انعكاس النقطة بالنسبة للدائرة ذات المركز .
إنشاء انعكاس لنقطة حول دائرة.

خصائص
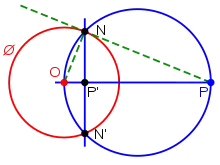
  • انعكاس دائرة مارة بمركز الدائرة أخرى حول الأخيرة، يُنتج خطاً مُستقيماً.
    انعكاس دائرة مارة بمركز الدائرة أخرى حول الأخيرة، يُنتج خطاً مُستقيماً.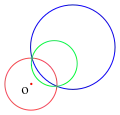
  • انعكاس الدائرة الخضراء هو الدائرة الزرقاء بالنسبة للدائرة الحمراء.
    انعكاس الدائرة الخضراء هو الدائرة الزرقاء بالنسبة للدائرة الحمراء.
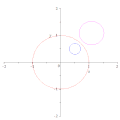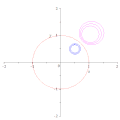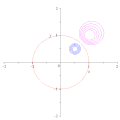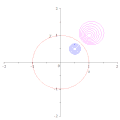  • التعاكس لا ينقل مراكز الدوائر إلى بعضها بعضاً.
    التعاكس لا ينقل مراكز الدوائر إلى بعضها بعضاً.

ينقل التعاكس كُل نقطة داخل الدائرة إلى صورةٍ نظيرةٍ لها خارجها، وكل نقطة تقع على محيط الدائرة فإنَّها تبقى كما هي. يُعبِّر هذا التحويل الهندسي عن اختزالٍ للصورة المستوى اللا نهائي الواقعة عليه الدائرة، بمعنى أنه كلما قربت النقطة من مركز الدائرة كُلمَّا كانت صورتها أبعد عن الدائرة، وكلَّما كانت النقطة بعيدة من مركز الدائرة فإن صورتها تُصبح أقرب لمركز الدائرة.[3]

في الهندسة الوصفية

فيما يلي مقارنة بين التحاكي (homothety ) والتعاكس (Inversion ) لجعل اثنين من المخروطيات اللامركزية متحدة المركز:[4]

معلوم اهليجيين ΔP و QΔ ، متشابهين وليس محوريين ولا متحدة المركز. المطلوب جعلهام متحدة المركز من خلال الهندسة الإسقاطية. للقيام بذلك ، يتم تثبيت أحداهما، على سبيل المثال ΔP، الذي يمثل الاهليج الخارجي ، ومن ثم يتم تحديد القطب I للخطين القطبين المتطابقين بالنسبة للاهليجين. يتم تحديد تعاكس I^ النقطة I (بالنسبة للاهليجين) كأقطاب متقارنة. بهذه الطريقة ، يمكننا جعل الاهليجين متحدتي المركز من خلال جعل I مركزًا للتحاكي (للأشكال الاهليجية المشابهة لـ ΔQ) من أجل تحجيم QΔ حتى يتزامن مركزه مع مركز ΔP. هذا الإجراء أسرع ولا يتطلب تحديد تعاكس ΔP و QΔ بالنسبة لاهليج ثالث Σ (مركزه النقطة I).

مقارنة بين التحاك (homothety ) والتعاكس (Inversion ) لجعل اثنين من المخروطيات اللامركزية متحدة المركز

معرض
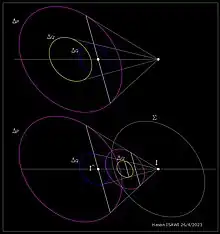
  • إنشاءات هندسية وصفية لعملية تعاكس ( inversion) دائرة زرقاء بالنسبة لدائرة أخرى صفراء، حيث الزرقاء لا تمر بمركز الصفراء. لمعرفة التطبيق انظر سلسلة شتاينر
    إنشاءات هندسية وصفية لعملية تعاكس ( inversion) دائرة زرقاء بالنسبة لدائرة أخرى صفراء، حيث الزرقاء لا تمر بمركز الصفراء. لمعرفة التطبيق انظر سلسلة شتاينر
  • Inversion transformation
    تحويل تعاكسي بين مخروطيتين متشابهتين
  • في الهندسة الوصفية يكمن الاختلاف الرئيسي في عمليتي التعاكس بين مخروطيتين متشابهتين او بين مخروطيتين غير متشابهتين
    في الهندسة الوصفية يكمن الاختلاف الرئيسي في عمليتي التعاكس بين مخروطيتين متشابهتين او بين مخروطيتين غير متشابهتين

انظر أيضاً

مراجع
  1. Altshiller-Court (1952, p. 230)
  2. Kay (1969, p. 264)
  3. Weisstein, Eric W. "Inversion". mathworld.wolfram.com (بالإنجليزية). Archived from the original on 2019-12-29. Retrieved 2020-03-11.
  4. The problem of tangency to three non-homothetic conics نسخة محفوظة 2023-01-03 على موقع واي باك مشين.

وصلات خارجية
  • أيقونة بوابةبوابة رياضيات
  • أيقونة بوابةبوابة هندسة رياضية
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.