تركيب الدوال
في الرياضيات, تركيب دالتين (بالإنجليزية: Function composition) هو إخضاع نتيجة الدالة الأولى للدالة الثانية.[2][3][4] أي أنه بالنسبة للدالتين f: X → Y و g: Y → Z, فإن تركيبهما هو حساب قيمة g ليس عندما يكون مدخلها هو x، بل عندما يكون مدخلها هو (f(x.ويعد موضوع تركيب الدوال مدخلا هاما في دراسة حساب التغيرات.
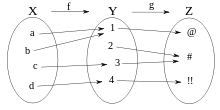
g ∘ f, تركيب الدالتين f و g. على سبيل المثال, (g ∘ f)(c) = #.
أمثلة
إذا كانت و , فإن و تُعرفان كما يلي، علما بأن هو رمز تركيب الدالتين:
خصائص
تركيب الدوال عادة ما يكون تجميعيا. f ∘ (g ∘ h) = (f ∘ g) ∘ h
انظر أيضًا
مراجع
- مذكور في: ISO 80000-2:2019 Quantities and units — Part 2: Mathematics. قسم أو آية أو فقرة أو بند: 2-12.11. الناشر: المنظمة الدولية للمعايير. تاريخ النشر: أغسطس 2019.
- Christopher Hollings (2014). Mathematics across the Iron Curtain: A History of the Algebraic Theory of Semigroups. American Mathematical Society. ص. 334. ISBN:978-1-4704-1493-1. مؤرشف من الأصل في 2019-06-12.
- Oleg A. Ivanov (1 يناير 2009). Making Mathematics Come to Life: A Guide for Teachers and Students. American Mathematical Soc. ص. 217–. ISBN:978-0-8218-4808-1. مؤرشف من الأصل في 2019-06-08.
- Nathan Carter (9 أبريل 2009). Visual Group Theory. MAA. ص. 95. ISBN:978-0-88385-757-1. مؤرشف من الأصل في 2013-04-30.
- بوابة تحليل رياضي
- بوابة رياضيات
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.