انتشار خلفي

الانتشار المُرتد[1] أو العكسي[2] أو الخلفي (بالإنكليزية: Backpropagation) هي إحدى طرق تعليم الشبكات العصبونية التي تؤمن نقل معلومات بالانتشار العكسي للاتجاه الأصلي لقدوم المعلومات.[3][4][5]

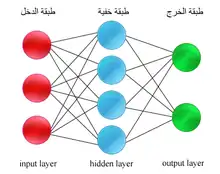
تعتمد هذه الطريقة على مبدأ التعليم المراقب وتحتاج في مرحلة التدريب إلى بيانات خاصة تتعلم بها الشبكة حيث تقدم لها بيانات دخل مع بيانات الخرج المرغوب فيها ومن ثم تقوم الشبكة بعمل انتشار امامي لبيانات الدخل للحصول على قيمة خرج الشبكة بعدها تقوم بالمقارنة بين الخرج المحسوب والخرج المرغوب فاذا لم تتطابق النتائج تقوم الشبكة بحساب قيمة الفرق بينهما لكل عصبون من طبقة الخرج والذي يمثل قيمة الخطا، بعدها تاتي مرحلة الانتشار المُرتد للأخطاء حيث تعيد الشبكة حساب قيمة الخطأ في كل عصبون من الشبكات الخفية. في الأخير تأتي مرحلة تحديث قيمة الأوزان حيث تقوم الشبكة بإعادة حساب كل الأوزان وتعوضها بالقيم الجديدة المحسوبة.

يشترط في الانتشار المُرتد ان تكون دوال التنشيط التي تستعملها العصبونات قابلة للاشتقاق. ذلك لانه في مرحلة تحديث الأوزان تستعمل الدالة المشتقة لدالة التنشيط في حساب القيم الجديدة.

طريقة التعليم

يمكن تقسيم مراحل التعليم التي تعتمد عليها الشبكة إلى مرحلتين :

  • المرحلة الأولى : الانتشار

مع كل عينة من بيانات الدخل يجب أن يتم :

  1. تغذية امامية للشبكة بعينة بيانات الدخل لحساب بيانات الخرج ومن ثم يتم مقارنة النتائج المحصل عليها مع النتائج المرغوب فيها ويتم حساب الفرق الذي يمثل قيمة الخطأ (error)
  2. تغذية مُرتدة حيث يتم حساب قيمة الخطأ في كل عصبون ينتمي للطبقات الخفية.
  • المرحلة الثانية : تحديث قيم الأوزان

يتم تحديث قيمة اوزان كل عصبون ينتمي إلى الطبقات الخفية (Hidden Layers)

تفاصيل خوارزمية الانتشار المُرتد

لنفهم كيفية عمل سنعتبر عصبون عصبونواحد. هذا العصبون يتلقى في الدخل بيانات (أرقام). قيمة الخرج لهذا العصبون هي مجموع موزون للارقام الداخلة. يعني كل رقم سيضرب في الوزن المنسوب لكل مشبك.

ثم هذا المجموع يقسم على مجموع الأوزان ليعطي قيمة الخرج للعصبون .

أولاً وقبل تدريب العصبون، الأوزان تعطى للمشابك بطريقة عشوائية. ثم يتم مد العصبون ببيانات الدخل والخرج.

العصبون سيحسب الخرج باعتبار بيانات الدخل والأوزان. طبعاً هذه الأوزان في أول الأمر عشوائية. بالتالي فإن الخرج المحسوب y لن يوافق الخرج الصحيح t.

مهمة العصبون بعد ذلك هي أن يغير الأوزان حتى يتحصل على خرج يوافق أو يقارب الخرج الصحيح.

طريقة حساب التفاوت بين القيمتان تعتمد على الخطأالتربيعي المتوسط خطأ تربيعي متوسط. ما يعادل E=(t-y)^2 \,,

لنأخذ المثال الذي يتلقى فيه العصبون (1,1) كبينات دخل و-0 كبيان خرج.

لو رسمنا تطور التفاوت E مع الخرج t سنحصل على سطح مكافئ .


التوافق في هذه الحالة وفي جميع الحالات هو القيمة الصغرى على السطح. عكسها على المحور اكس يعطي القيمة الاقرب للخارج الصحيح.

هذا بنسبة لعصبون بسيط. أما بنسبة لشبكات المركبة، وهي ما يستعمل دائما فإنها ستكون إيجاد القيمة الصغرى ولكن لعمليات أكتر تعقيدا.

مراجع
  1. موفق دعبول؛ مروان البواب؛ نزار الحافظ؛ نوار العوا (2017)، قائمة مصطلحات المعلوماتية (بالعربية والإنجليزية)، دمشق: مجمع اللغة العربية بدمشق، ص. 17، QID:Q112244705
  2. معجم البيانات والذكاء الاصطناعي (PDF) (بالعربية والإنجليزية)، الهيئة السعودية للبيانات والذكاء الاصطناعي، 2022، ص. 44، QID:Q111421033
  3. "Who Invented the Reverse Mode of Differentiation? - Semantic Scholar". www.semanticscholar.org (بالإنجليزية الأمريكية). Archived from the original on 2019-12-13. Retrieved 2017-08-04.
  4. LeCun، Yann؛ Bengio، Yoshua؛ Hinton، Geoffrey (2015). "Deep learning". Nature. ج. 521: 436–444. DOI:10.1038/nature14539. PMID:26017442.
  5. Dreyfus، Stuart. "The numerical solution of variational problems". Journal of Mathematical Analysis and Applications. ج. 5 ع. 1: 30–45. DOI:10.1016/0022-247x(62)90004-5. مؤرشف من الأصل في 2018-09-13.
  • أيقونة بوابةبوابة علم الحاسوب
  • أيقونة بوابةبوابة روبوتيات
  • أيقونة بوابةبوابة إحصاء
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.