الدالة المعدة للأعداد الأولية
في الرياضيات، الدالة المعدة للأعداد الأولية (بالإنجليزية: Prime-counting function) هي دالة تعد عدد الأعداد الأولية الأصغر من أو المساوية لعدد حقيقي ما.[1][2][3] عادة ما يرمز إليها ب (في هذه الإشارة، لا يشير إلى العدد π).

التاريخ
في نهاية القرن الثامن عشر، حدس كل من كارل فريدريش غاوس وأدريان ماري ليجاندر أن الدالة المعدة للأعداد الأولية تساوي بالتقريب:
هذا يعني ما يلي:
يطلق على هاته المتساوية اسم مبرهنة الأعداد الأولية. هناك متساوية أخرى متكافئة وهي:
حيث li هي دالة التكامل اللوغاريتمي. بُرهن لأول مرة على هذه المبرهنة في عام 1896. كان ذلك من طرف كل من العالمين جاك هادامار وشارل جون دو لا فالي بوسان، الواحد منهما بمعزل عن اللاخر.
لائحة قيم (π(x و(x / ln(x و(li(x
تظهر هذه اللائحة قيم الدوال الثلاث (π(x و(x / ln(x و(li(x عند قوى العدد عشرة.
x π(x) π(x) − x / log x li(x) − π(x) x / π(x) x / log x % Error 10 4 0 2 2.500 -8.57% 102 25 3 5 4.000 13.14% 103 168 23 10 5.952 13.83% 104 1,229 143 17 8.137 11.66% 105 9,592 906 38 10.425 9.45% 106 78,498 6,116 130 12.739 7.79% 107 664,579 44,158 339 15.047 6.64% 108 5,761,455 332,774 754 17.357 5.78% 109 50,847,534 2,592,592 1,701 19.667 5.10% 1010 455,052,511 20,758,029 3,104 21.975 4.56% 1011 4,118,054,813 169,923,159 11,588 24.283 4.13% 1012 37,607,912,018 1,416,705,193 38,263 26.590 3.77% 1013 346,065,536,839 11,992,858,452 108,971 28.896 3.47% 1014 3,204,941,750,802 102,838,308,636 314,890 31.202 3.21% 1015 29,844,570,422,669 891,604,962,452 1,052,619 33.507 2.99% 1016 279,238,341,033,925 7,804,289,844,393 3,214,632 35.812 2.79% 1017 2,623,557,157,654,233 68,883,734,693,928 7,956,589 38.116 2.63% 1018 24,739,954,287,740,860 612,483,070,893,536 21,949,555 40.420 2.48% 1019 234,057,667,276,344,607 5,481,624,169,369,961 99,877,775 42.725 2.34% 1020 2,220,819,602,560,918,840 49,347,193,044,659,702 222,744,644 45.028 2.22% 1021 21,127,269,486,018,731,928 446,579,871,578,168,707 597,394,254 47.332 2.11% 1022 201,467,286,689,315,906,290 4,060,704,006,019,620,994 1,932,355,208 49.636 2.02% 1023 1,925,320,391,606,803,968,923 37,083,513,766,578,631,309 7,250,186,216 51.939 1.93% 1024 18,435,599,767,349,200,867,866 339,996,354,713,708,049,069 17,146,907,278 54.243 1.84% 1025 176,846,309,399,143,769,411,680 3,128,516,637,843,038,351,228 55,160,980,939 56.546 1.77% 1026 1,699,246,750,872,437,141,327,603 28,883,358,936,853,188,823,261 155,891,678,121 58.850 1.70% 1027 16,352,460,426,841,680,446,427,399 267,479,615,610,131,274,163,365 508,666,658,006 61.153 1.64% 1028 157,589,269,275,973,410,412,739,598 2,484,097,167,669,186,251,622,127 1,427,745,660,374 63.456 1.58% 1029 1,520,698,109,714,272,166,094,258,063 23,130,930,737,541,725,917,951,446 4,551,193,622,464 65.759 1.52%
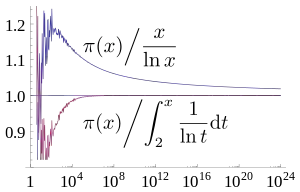
خوارزميات من أجل تحديد (π(x
تكمن الطريقة الأكثر بساطة من أجل تحديد (π(x إذا لم يكن x كبيرا جدا، في استعمال غربال إراتوستينس من أجل تحديد لائحة الأعداد الأولية الأصغر من x، وبذلك عدها.
هناك طريقة أكثر تطورا وتعود إلى ليجاندر.
دوال أخرى تمكن من عد الأعداد الأولية
انظر إلى تحويل ميلين وإلى دالة فون مانغولدت وإلى صيغة القلب لموبيوس وإلى دالة زيتا لريمان وإلى صيغة بيرون.
صيغ تحققها الدوال المعدة للأعداد الأولية
حيث
انظر أيضا
مراجع
- إيريك ويستاين، Prime Counting Function، ماثوورلد Mathworld (باللغة الإنكليزية).
- إيريك ويستاين، Gram Series، ماثوورلد Mathworld (باللغة الإنكليزية).
- "Tables of values of pi(x) and of pi2(x)". Tomás Oliveira e Silva. مؤرشف من الأصل في 2006-08-24. اطلع عليه بتاريخ 2008-09-14.
وصلات خارجية
- بوابة رياضيات
- بوابة تحليل رياضي
- بوابة نظرية الأعداد