استيفاء الجار الأقرب

استيفاء الجار الأقرب (بالإنجليزية: Nearest-neighbor interpolation) (المعروف أيضًا باسم الاستيفاء الداني أو في بعض السياقات، معاينة النقطة) عبارة عن طريقة بسيطة لاستيفاء متعدد الأبعاد في بُعدٍ واحد أو أكثر.[1]

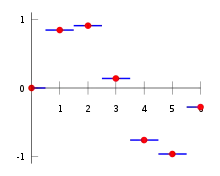
استيفاء الجار الأقرب (الخطوط الزرقاء) في بعد واحد على مجموعة البيانات (النقاط الحمراء) بتوزيع متساوٍ
استيفاء الجار الأقرب على شبكة ثنائية الأبعاد متجانسة (النقاط السوداء). كل خلية ملونة تشير إلى المنطقة التي تكون فيها جميع النقاط مع النقطة السوداء داخل الخلية هي أقرب نقطة سوداء إليها.

الاستيفاء هو مسألة تقريب قيمة دالة لنقطة غير معطاة في الفضاء عندما يتم توفير قيمة تلك الدالة في النقاط المحيطة (المجاورة) لتلك النقطة. تقوم خوارزمية الجار الأقرب باختيار قيمة النقطة الأقرب ولا تأخذ في الاعتبار قيم النقاط المجاورة على الإطلاق، مما ينتج عنه استيفاء ثابت مقطعي. الخوارزمية سهلة جدًا في التنفيذ وتُستخدم بشكل شائع (عادة مع mipmapping) في التصيير ثلاثي الأبعاد في زمن حقيقي لتحديد قيم الألوان لسطح مكسي.

العلاقة بمخطط فورونوي

بالنسبة لمجموعة معينة من النقاط في الفضاء، مخطط فورونوي هو تقسيم للفضاء إلى خلايا، خلية واحدة لكل نقطة معينة، بحيث في أي مكان في الفضاء، النقطة المعطاة الأقرب تكون داخل الخلية. هذا يعادل استيفاء الجار الأقرب، من خلال تعيين قيمة الدالة في النقطة المعطاة لجميع النقاط داخل الخلية. الأشكال على الجانب الأيمن يظهر باللون شكل الخلايا.

مقارنة بين الاستيفاء أحادي البعد وثنائي البعدين
أسود وأحمر/أصفر/أخضر/أزرق تتناسب النقاط مع نقطة الاستيفاء والعينات المجاورة، على التوالي.
وتتناسب ارتفاعاتهم عن سطح الأرض مع قيمهم.
هذا مخطط فورونوي هو مثال على استيفاء الجار الأقرب لمجموعة عشوائية من النقاط (النقاط السوداء) في البُعد الثنائي.


أنظر أيضا

المراجع
  1. Alejandro F. Frangi, Jerry L. Prince and Milan Sonka (2023). Medical Image Analysis (بالإنجليزية). Mara Conner. p. 137. ISBN:978-0-12-813657-7.
  • أيقونة بوابةبوابة تحليل رياضي
  • أيقونة بوابةبوابة رياضيات
  • أيقونة بوابةبوابة علم الحاسوب
  • أيقونة بوابةبوابة هندسة رياضية
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.