اختبار تجريبي لتمدد الوقت

مخطط مينكوفيسكي

أ) المشاهدة في S

ب) المشاهدة في S'

ج) مخطط لويديل (لجعل الاختلافات أصغر، استُخدم 0.7c بدلًا من 0.995c)

إن سبب ظهور الميونات هو تصادم الأشعة الكونية الأتية من أعماق الكون مع الغلاف الجوي العلوي للأرض ، بعد ذلك تصل الميونات إلى سطح الأرض. يعتمد احتمال وصول الميونات إلى الأرض على نصف عمرها الذي يُعدّل عن طريق التصحيحات النسبية في الوضعين : أ) متوسط عمر الميونات المتحركة بسرعة قريبة من سرعة الضوء و عمر الميونات الموجودة في المختبر وتعتبر غير متحركة ب) . وهذا يسمح بالتطبيق المباشر لتقلص طول الزمن للميونات المتخللة الغلاف الجوي بالمقارنة لزمن تحلل الميونات الموجودة في المختبر على الأرض.[1][2]

تمدد الوقت وتقلص الطول

طول الغلاف الجوي: تُعطى صيغة الانكماش بواسطة ${\displaystyle L=L_{0}/\gamma }$، حيث L₀ هو طول السكون للغلاف الجوي وL هو طوله المتقلص. بما أن الغلاف الجوي في حالة سكون في S، لدينا γ=1 ويُقاس طول السكون L₀. وبما أنه في حالة حركة في S'، لدينا γ>1 ويُقاس طوله المتقلص L′.

وقت تحلل الميونات: صيغة تمدد الوقت هي ${\displaystyle T=\gamma \ T_{0}}$، حيث T₀ هو الوقت المناسب على مدار الساعة للميون، وهذا يتوافق مع متوسط وقت تحلل الميون في إطاره الصحيح. بما أن الميون في حالة سكون في S'، لدينا γ=1 ويُقاس وقته المناسب T′₀. وبما أنه يتحرك في S، لدينا γ>1، ولذلك يكون الوقت المناسب أقصر بالنسبة إلى الوقت T. (على سبيل المقارنة، يمكن أخذ ميون آخر على الأرض بعين الاعتبار، يُسمى الميونS-، لذلك يكون وقت التحلل في S أقصر من الميونS-، بينما يكون أطول في S').

• في S، يتوفر لدى الميونS'- وقت اضمحلال أطول من الميونS-، لذلك يوجد لدى الميونS'- وقت كافٍ لتمرير الطول المناسب للغلاف الجوي للوصول إلى الأرض.
• في S'، يتوفر لدى الميونS- وقت اضمحلال  أطول من الميونS-. ولكن هذه ليست المشكلة، بما أن الغلاف الجوي يتقلص مع طوله المناسب. لذلك، فحتى وقت التحلل الأسرع في الميونS'- يكفي لكي يمر عبر الغلاف الجوي المتحرك للوصول إلى الأرض.

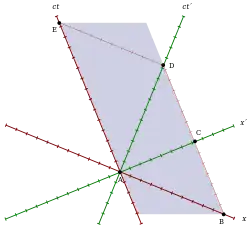
مخطط مينكوفسكي

يظهر الميون في (A) عن طريق تصادم الإشعاع مع الغلاف الجوي العلوي. إن الميون في حالة سكون في S'، لذا فإن خطه العالمي هو المحور ct'. وإن الغلاف الجوي العلوي في حالة سكون في S، لذا فإن خطه العالمي هو المحور ct. عند محوريّ x وx'، كل الأحداث موجودة متزامنة مع A في S وS'، على الترتيب. يلتقي الميون والأرض في D. بما أن الأرض في حالة سكون في S، يُرسم خطها العالمي (المطابق للغلاف الجوي السفلي) موازيًا للمحور ct، حتى يتقاطع مع محوري x وx'.

الوقت: إن الفاصل الزمني بين حدثين من الأحداث الموجودة في العالم على مدار الساعة يُسمى الوقت المناسب، وذلك أمر مهم في النسبية الخاصة. بما أن أصل الميون في A يواجه الأرض في D على الخط العالمي للميون، فإن ما يستطيع أن يشير إلى الوقت المناسب T′₀=AD هو فقط ساعة تترافق مع الميون وبالتالي تكون في حالة سكون في S. كذلك في S، اتُّفق على أن هذه الساعة تشير إلى الوقت المحدد بين الأحداث، ولأنها تكون في حالة حركة هنا، فإن T′₀=AD  يكون أقصر من الوقت T المشار إليه في الساعات الساكنة في S، ويمكن ملاحظة ذلك على فترات زمنية أطول T=BD=AE موازية للمحور ct.

الطول: يتوافق الحدث B، حيث يتقاطع الخط العالمي للأرض مع المحور x، في S مع موضع الأرض في وقت متزامن مع ظهور الميون. أما C، حيث يتقاطع الخط العالمي للأرض مع المحور x، فيتوافق في S' مع موضع الأرض في وقت متزامن مع ظهور الميون. يكون الطول L₀=AB في S أطول من الطول L′=AC في S'.

نتائج تجربة فريتش- سميث. إحصاء المنحنيات بالنسبة إلى ${\displaystyle M_{\mathrm {Newton} }}$ و${\displaystyle M_{\mathrm {SR} }}$.

إذا لم يكن هناك تمدد زمني، فيجب أن تتحلل هذه الميونات في الغلاف الجوي العلوي، ونتيجة لتمدد الزمن، فإنها موجودة بكميات كبيرة أيضًا على ارتفاعات أقل بكثير من ذلك. تسمح مقارنة هذه الكميات بتحديد متوسط العمر الافتراضي وأيضًا عمر النصف للميونات. ${\displaystyle N}$ هو عدد الميونات المقاسة في الغلاف الجوي العلوي، و${\displaystyle M}$ على مستوى سطح البحر، و${\displaystyle Z}$ هو وقت السفر في الإطار المتبقي للأرض الذي تقطع به الميونات المسافة بين تلك المناطق، و${\displaystyle T_{0}}$ هو متوسط العمر المناسب للميونات.[3]

${\displaystyle {\begin{aligned}M_{\mathrm {Newton} }&=N\exp \left[-Z/T_{0}\right]\\M_{\mathrm {SR} }&=N\exp \left[-Z/\left(\gamma T_{0}\right)\right]\end{aligned}}}$

في عام 1940، وفي بحيرة إيكو ليك (3240 م) ودنفر في كولورادو (1616 م)، قاس برونو روسي وَدي. بي. هول الانحلال النسبي للميوونات (التي اعتقدا أنها ميزونات). قاسا الميونات في الغلاف الجوي في أثناء السفر بسرعة أكبر من 0.99 c (c هي سرعة الضوء). أكد روسي وهول صيغ الزخم النسبي وتمدد الوقت بطريقة نوعية. مكّنتهما معرفة نظرية الزخم وعمر الميونات المتحركة من حساب متوسط عمرها المناسب؛ توصلا إلى ≈ 2.4 ميكروثانية (حسنت التجارب الحديثة هذه النتيجة لتصبح ≈ 2.2 ميكروثانية).[4][5][6][7]

أُجريت تجربة أدق من هذا النوع على يد ديفيد إتش. فريش وسميث (1963)، اللذين قاسا نحو 563 ميونًا في الساعة في ستة أشواط على جبل واشنطن. من خلال قياس الطاقة الحركية، حُدد متوسط سرعات الميون بين 0.995 c و0.9954 c. كان الهدف يقع في كامبريدج، ماساتشوستس مع اختلاف في الارتفاع يبلغ 1907 م، والذي ينبغي اجتيازه من قبل الميونات في 6.4 ميكروثانية تقريبًا. بافتراض عمر متوسط قدره 2.2 ميكروثانية، لن يصل إلى هذا الموقع سوى 27 ميونًا إن لم يكن هناك تمدد في الوقت، ومع ذلك، وصل ما يقارب 412 ميونًا في الساعة إلى كامبريدج، ما أدى إلى عامل تمدد زمني يبلغ8.8 ± 0.8 .

أظهر كل من فريتش وسميث أن هذا يتفق مع توقعات النسبية الخاصة: يبلغ عامل التمدد الزمني للميونات في جبل واشنطن المسافرة بسرعات بين 0.995 c إلى 0.9954 c حوالي 10.2. تضاءلت طاقتها الحركية ومن ثم سرعتها حتى وصلت إلى كامبريدج لتصبح0.9881 c  و0.9897 c بسبب التفاعل مع الغلاف الجوي، ما قلل عامل التمدد إلى 6.8. لذلك بين البداية (  10.2) والهدف (  6.8)، حُدد عامل تمدد وقت متوسط يبلغ ±8.4 بواسطتهما وبالاتفاق مع النتيجة المقاسة ضمن الأخطاء (انظر إلى الصيغ وصور حساب منحنيات التحلل أعلاه).[8]

تجارب أخرى

أُجريت منذ ذلك الحين العديد من القياسات لمتوسط العمر الافتراضي للميونات في الغلاف الجوي وتمدد الوقت في تجارب المرحلة الجامعية.[3][9]

أُجريت قياسات أكثر دقة لتحلل الجسيمات في مسرّعات الجسيمات باستخدام الميونات وأنواع مختلفة من الجسيمات. إلى جانب تأكيد تمدد الوقت، أُكّد تناظر سي بّي تي أيضًا من خلال مقارنة عمر الجسيمات الموجبة والسالبة. يتطلب هذا التناظر أن تكون معدلات تحلل الجزيئات والجسيمات المضادة لها كما هي، إذ إن انتهاك تناظر سي بّي تي يؤدي إلى انتهاك تناظر لوريتنز أيضًا وبالتالي النسبية الخاصة.

يجري الآن تأكيد تمدد الوقت للجسيمات بشكل روتيني في مسرعات الجسيمات إلى جانب اختبارات الطاقة النسبية والزخم، ويُعد إلزاميًا في تحليل تجارب الجسيمات في السرعات النسبية.

في عام 1977، قاس بيلي وأخرون عمر الميونات الإيجابية والسلبية المرسلة حول حلقة التخزين الميونات في سيرن . أكدت هذه التجربة أن كلًا من تمدد الوقت ومفارقة التوأم، إي الفرضية القائلة إن الساعات المرسلة والعائدة إلى وضعها الأولي تتباطأ بالنسبة إلى ساعة ساكنة.[27][28] هناك قياسات أخرى من مفارقة التوأم تنطوي على جاذبية تمدد الوقت أيضًا.

في تجربة كيتينج - هافيليه، نُقلت الساعات الذرية الفعلية لشعاع السيزيوم حول العالم، وعُثر على الاختلافات المتوقعة مقارنة بالساعة الثابتة.

تنص فرضية الساعة على أن مدى التسارع لا يؤثر على قيمة تمدد الوقت. في معظم التجارب التي ذُكرت سابقًا، كانت الجسيمات المتحللة في إطار القصور الذاتي، أي غير متسارعة. ومع ذلك، في بيلي وآخرون (1977)، كانت الجسيمات معرضة لتسارع عرضي يصل إلى ~10¹⁸ g. ولما كانت النتيجة نفسها، تبين أن التسارع ليس له تأثير على تمدد الوقت.[27] بالإضافة إلى ذلك، قاس روس وآخرون (1980) انحطاط باريجونات سيجما، التي كانت معرضة لتسارع طولي بين 0.5×10¹⁵ g و 5.0×10¹⁵ g. ومرة أخرى، لم يُقَس أي انحراف عند تمدد الوقت العادي.[29]