Iste articlo ye en proceso de cambio enta la ortografía oficial de Biquipedia (la Ortografía de l'aragonés de l'Academia Aragonesa d'a Luenga). Puez aduyar a completar este proceso revisando l'articlo, fendo-ie los cambios ortograficos necesarios y sacando dimpués ista plantilla.

Integral de Riemann

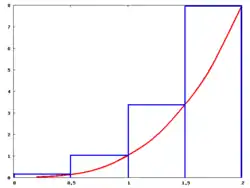
En matematicas, a integración se relaciona con dos problemas clasicos de l'analís matematica, que no pareixen relacionatos:

• O calculo d'arias y volumens, y l'acción que una función d'una u cuantas variables les aplica a las rechions debant ditas.
• A obtención d'a primitiva d'una función, isto ye, trobar a función que a suya derivata ye a función dada, estando a "operación inversa" a la derivación

Os estudios de Isaac Barrow, Isaac Newton y Gottfried Leibniz, dioron forma a lo teorema fundamental d'o calculo, que amuestra la intima relación en a solución d'istos dos problemas. Se clama integración definita a la obtención de l'aria baixo una curva, y integración indefinita a la operación inversa d'a derivación. Tamién se diz integración a la resolución d'una ecuación diferencial, una ecuación en a que a incognita ye una u cuantas funcions y as suyas derivatas.

Integral indefinita

Dada una función F(x) tal que a suya derivata ye F'(x) = f(x), allora decimos que F ye a integral u primitiva de f, definindo asinas a integración como a inversa d'a derivación. Simbolicament se denota por

${\displaystyle F(x)=\int f(x)dx}$

Una función dada no tien una sola integral indefinita. Por eixemplo, ta la función ${\displaystyle f(x)=x+2}$, as siguients funcions son todas primitivas d'a mesma:

${\displaystyle {\begin{matrix}F_{1}(x)={\frac {1}{2}}x^{2}+2x\\F_{1}(x)={\frac {1}{2}}x^{2}+2x+{\frac {3}{2}}\\F_{1}(x)={\frac {1}{2}}x^{2}+2x+\pi \end{matrix}}}$

En cheneral, si F(x) ye una primitiva de f(x), allora cualsiquier función d'a forma F(x)+c, estando c una constant cualsiquiera, ye tamién una primitiva de f(x).

Integral definita

Integral definita, vista como l'aria d'a rechión baixo una curva

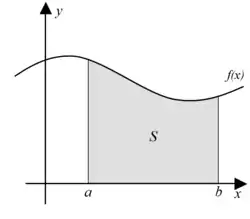
Dada una función:

${\displaystyle y=f(x)\,}$

se define a integral definita entre a y b d'a función f como l'aria S y se denota por:

${\displaystyle S=\int _{a}^{b}f(x)dx}$

Si se tien una primitiva (integral indefinita) d'a función f:

${\displaystyle \int f(x)dx=F(x)}$

allora

${\displaystyle S=F(b)-F(a)\,}$

a ista relación entre a integral indefinita y a superficie baixo a función le se clama Teorema fundamental d'o calculo integral.

O desarrollo d'a Teoría d'a mida en a Matematica ha produciu historicament diversas definicions d'o concepto d'integral

• A Integración u Sumas de Riemann, a mas conoixita.
• A integración de Lebesgue, mas cheneral pero considerablement mas abstracta, por lo que difuera d'os usos propiament academicos se limita a sobén o estudio d'o calculo integral a los relacionatos con a integral de Riemann, mas intuitiva y suficient ta la mayoría d'as aplicacions practicas.

Se veiga tamién

• Integración numerica.

Vinclos externos

• Resolución d'integrals online