ፓይ

ፓይ ወይም በተለምዶ አጻጻፉ π የሚታወቀው ቁጥር የማንኛውም ክብ መጠነ ዙሪያ ለወገብ ርዝመት (ዲያሜትሩ) ሲካፈል የሚገኘው ምንጊዜም የማይቀየረው ቋሚ ቁጥር ነው።

የክቡ አቋራጭ መስመር አንድ ከሆነ መጠነ ዙሪያው ፓይ እንደሚሆን የሚያሳይ ምስል

የፓይን እርግጠኛ ዋጋ ማወቅ ባይቻለም ከ 3.141593 እንደሚጠጋ ግን በሂሳብ ስሌት የተደረሰበት ጉዳይ ነው። የፈለግነውን ሁለት ሙሉ ቁጥሮች አካፍለን ፓይን ማግኘት ስለማንችል ኢራሽናል ቁጥር ነው ማለት ነው። በዚህ ምክንያት ፓይ በነጥብ ስርዓት (decimal system) ሲጻፍ አሃዞቹ ወይም አያበቁም ወይም ደግሞ እራሳቸውን አይደግሙም ፣ ይልቁኑ በማያባራ ዘፈቀደ ሁኔታ ይነጉዳሉ። ይህን ጉዳይ እታች በበለጠ እናየዋለን።

መሰረታዊ ሃቆች

የፓይ ፊደል π
የπ ምልክት

በሌላ በኩል ደግሞ ሙሉ ቁጥሮችን በተወሰኑ የመደመረ መቀነስ ማካፈል ማባዛት ክፍ ማድርገና ስኩዌር እና ኩቢክ ሩት በመውስድ ፓይን ማግኘግ ስለማንችል ታራንስዴንታል ቁጥር ተብላላለች። ይህን ሁኔታ ያረጋገጡት በ19ኛው ክፍለ ዘመን የነበር የጀርመን ሂሳብ ተማሪወች ሲሆኑ ጥናቱ እንደ ትልቅ ድል እስካሁን ሲወሳ ይኖርል። በነገራችን ላይ ፓይ (π) የሚለውን ፊደል ለ ዚህ ቁጥር ያዋለው የኤንግሊዙ ተማሪ ዊልያም ጆንዝ በ1707 ነበር የወሰደውም ከግሪኩ ቃል "περίμετρος" (የክብ መጠነ ዙሪያ ማለት ነው)"[1] ።

የጆሜትሪ ትርጉሙ
  • መጠነ ዙሪያ = π × ዲያሜትር
    መጠነ ዙሪያ = π × ዲያሜትር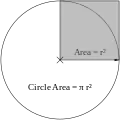
  • የክቡ መጠነ ስፋት = π ጊዜ የጠቆረው አራት ማእዘን ስፋት
    የክቡ መጠነ ስፋት = π ጊዜ የጠቆረው አራት ማእዘን ስፋት
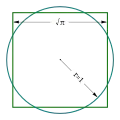  • አረንጓዴውን አራአት ማእዘን በማስመሪያና በኮምፓስ ማግኘት አይቻልም
    አረንጓዴውን አራአት ማእዘን በማስመሪያና በኮምፓስ ማግኘት አይቻልም

π እንግዲህ የክብ መጠነ ዙሪያ C ለ ወገብ ርዝመት d ስናካፍል የምናገኘው ቋሚ ቁጥር ነው። ክቡ ይነስም ይብዛ ይህ ቁጥርም ምንጊዜም አንድ ነው።:[1]

በሌላ አንጻር ፓይ የክቡ መጠነ ስፋት ለአቋራጭ መስመሩ ግማሽ (radius) ስኴር ሲካፈል የምንገኘው ቋሚ ቁጥርን ነው። አሁንም የክቡ ትልቅነት ወይም ትንሽነት ለዚህ ውድር(ratio) ምንም ለውጥ አያመጣም።

በነጥብ ሲጻፍ

የመጀመሪያወቹ የ ፓይ ሓምሳ ቁጥሮች ሲዘረዘሩ ይህን ይመስላሉ...

እርግጥ ነው ከዚ በላይ ሰወች የፓይን የአሃዝ ዝርዝር አስልተዋል አንዳንዶች እስከ መቶ ሌሎች እስክ ሚሊየን እና ቢሊየን በኮምፒውተር ትግዘው ለማስላት ችለውል። በአሁኑ ስዓት ከሁሉ በላይ በማስላት ማእርጉን የያዘው የፓይን አሃዞች ከትሪሊየን በላይ (1012) ቁጥሮች,[2] በማግኘት ነው። ይሁንና ማንኛውንም መሬት ያለን ክብ መጠነ ዙርያ ለማግኘት ከ11 አሃዞች በላይ አያስፈልገንም። በአይን የሚተያውን ህዋ በሙሉ የሚያዳርስ ክብንም ለመለካት ከ39 በላይ የፓይ አሃዞች አያስፈልጉንም [3][4]

የ π ዋጋ ሲገመት
የቁጥር ስርዓት የ ግምቶች
ባይናሪ መለጠፊያ:Gaps
ዴሲማል መለጠፊያ:Gaps
ሄክሳዴሲማል መለጠፊያ:Gaps
ቀጣይ ክፍልፋዮች 3, 22⁄7, 333⁄106, 355⁄113, 103993/33102, ...
ቀጣይ ክፍልፋዮች [3;7,15,1,292,1,1,1,2,1,3,1,14,2,1,1...][5]
3.1415926535 8979323846 2643383279 5028841971 6939937510

5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989 3809525720 1065485863 2788659361 5338182796 8230301952 0353018529 6899577362 2599413891 2497217752 8347913151 5574857242 4541506959

ፓይ እክሰ 1120 አሃዙ ድረስ የተገመተበት ሲሆን ያለ ኮምፒዩተር በእጅ ካሉኩሌተር ብቻ የተሰላ ነው[6]

የጥንቶቹ ግምት ግን 3 ነበር ። በመስጽሃፍ ቅዱስም ይህ ሲሰራበት ይታያል። ነገር ግን ትክክለኛው ዋጋ ከ3 ይበላጣል።

  1. "About Pi". Ask Dr. Math FAQ. በ2007-10-29 የተወሰደ.
  2. "Current publicized world record of pi". Archived from the original on 2011-03-12. በ2007-10-14 የተወሰደ.
  3. Young, Robert M. (1992). Excursions in Calculus. Washington: Mathematical Association of America (MAA). p. 417. ISBN 0883853175. http://books.google.com/books?id=iEMmV9RWZ4MC&pg=PA238&dq=intitle:Excursions+intitle:in+intitle:Calculus+39+digits&lr=&as_brr=0&ei=AeLrSNKJOYWQtAPdt5DeDQ&sig=ACfU3U0NSYsF9kVp6om4Zyw3a7F82QCofQ.
  4. "Statistical estimation of pi using random vectors". በ2007-08-12 የተወሰደ.
  5. መለጠፊያ:OEIS2C: Continued fraction for Pi, On-Line Encyclopedia of Integer Sequences
  6. Wrench, John. "The evolution of extended decimal approximations to π", The Mathematics Teacher, volume 53, pages 644–650 (1960).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.