የካልኩለስ መሰረታዊ እርግጥ

የካልኩለስ መሰረታዊ እርግጥ በሁለቱ ታላላቅ የካልኩለስ ክፍሎች፣ ማለትም በውድድር እና ጥርቅም (ጥረዛ) መካከል ያለውን ዝምድና የሚወስን የሒሳብ መሰረታዊ እርግጥ ነው።

በቀይ የተቀባው ክፍል ስፋት በ h times ƒ(x) ሊገመት ይችላል። ወይንም ደግሞ, የስፋት አስረካቢው A(x) ቢታዎቅ ኖሮ፣ እንዲህ ሊሰላ ይችላል A(x + h) − A(x). እኒህ ሁለቱ ብዘቶች ከሞላ ጎደል እኩል ናቸው፣ በተለይ h በጣም ትንሽ ከሆነ

መሰረታዊ እርግጡ በሁለት ይከፈላል።

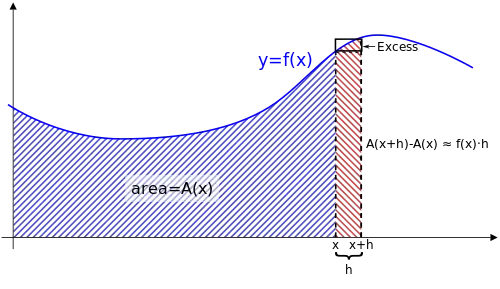
የመጀመሪያው ክፍል፣ በአንድ አስረካቢ ላይ የሚካሄድ ውስን ያልሆነ መጠራቀምን በ ውድድር ሊመለስ እንደሚችል ያሳያል።

ሁለተኛው ክፍል የአንድን አስረካቢ ውስን ጥርቅም፣ በመደመር ሳይሆን፣ ኢውድድሩን በማስላት ለማግኘት ያስችላል።

የካልኩለስ መሰረታዊ እርግጥን መጀመሪያ ያገኘው የስኮትላንድ ተወላጁ ጄምስ ግሪጎሪ ሲሆን፣ በኋላም ኢሳቅ ባሮው፣ ተማሪው ኢሳቅ ኒውተን እና ጎትፍሪድ ሌብኒዝ እርጉጡን በማስፋፋትና በማብራራት ስማቸው ይጠራል።

መሰረታዊው እርጉጥ ሁለት ክፍሎች አሉት። የመጀመሪያው ክፍል፣ የኢውድድርን ውድድር በማግኘት ላይ ሲያተኩር፣ ሁለተኛው ክፍል፣ በኢውድድርና በጥረዛ ላይ ያተኩራል

የመጀመሪያው ክፍል

ይህ ክፍል ብዙ ጊዜ የመጀመሪያው የካልኩለስ መሰረታዊ እርግጥ ተብሎ ይታወቃል.[1]

f በ ዝግ ወሰኖች [a, b] መካከል ሪጋ (የማይቋረጥ) አስረካቢ ነው እንበል።እንዲሁ አስረካቢ F በዝግ ወሰኖች[a, b] በሚገኙ ማናቸውም x ላይ እንዲህ ቢተረጎም

F(x)=\int _{a}^{x}f(t)\,dt\,.

F በወሰኖች [a, b] ተወዳዳሪ ሪጋ አስረካቢ ከመሆኑም በላይ, በክፍት ወሰኖች (a, b) ውስጥ ውድድሩ እንዲህ ይሰላል

F'(x)=f(x)\,

\qquad x\in (a,b).

ማረጋገጫ

{\begin{aligned}F^{\prime }(x)&=\lim _{h\rightarrow 0}{\frac {F(x+h)-F(x)}{h}}=\lim _{h\rightarrow 0}{\frac {1}{h}}{\biggl (}\int _{a}^{x+h}f(t)\,dt-\int _{a}^{x}f(t)\,dt{\biggr )}\\&=\lim _{h\rightarrow 0}{\frac {1}{h}}\int _{x}^{x+h}f(t)\,dt=\lim _{h\rightarrow 0}f(c)=\lim _{c\rightarrow x}f(c)=f(x).\end{aligned}}

የመጀመሪያው ደረጃ፣ የውድድርን ትርጓሜ ይጠቀማል፣ ሁለተኛው ደረጃ የ F ን ትርጉም ይጠቀማል። ሶስተኛው ደረጃ የአጠራቃሚን የመደመር ባህሪ ይጠቀማል። . አራተኛው ደረጃ የማዕከላዊ ዋጋ እርግጥን ይጠቀማል፡፡ አምስተኛው ደረጃ c በ x እና x + h መካከል መገኘቷን ሲጠቀም፣ የመጨረሻው ደረጃ፣

f

ሪጋ አስረካቢ መሆኑን ይጠቀማል።

ምሳሌዎች

F(x)=\int _{0}^{x}t^{2}dt\Rightarrow F'(x)=x^{2}

H(x)=\int _{10}^{e^{3x}}t^{2}dt\Rightarrow H'(x)=F'({e^{3x}})*{e^{3x}}'\Rightarrow H'(x)={e^{3x*2}}e^{3x}3=3e^{9x}

G(x)=\int _{0}^{x^{2}}\arcsin(t)dt\Rightarrow G'(x)=\arcsin(x^{2})2x

ሁለተኛው ክፍል

ይሄ ክፍል ሁለተኛው የካልኩለስ መሰረታዊ እርግጥ ተብሎ ሲታዎቅ [2] በአንዳንዶች ዘንድ የኒውተን-ሌብኒዝ እርግጥ ተብሎ ይታዎቃል።

ƒ የእውን ቁጥር አሰረካቢ እና በተዘጉ ወሰኖች [a, b] መካከል ይተተረጎመ ቢሆን፣ እና ኢውድድሩ g በወሰኖች[a, b] የተገኘ ቢሆን። በሌላ አነጋገር ƒ እና g አስረካቢዎች ቢሆኑና በወሰኖች [a, b] መካከል ለሚገኙ ማናቸውም x እንዲህ ቢተረጎሙ

f(x)=g'(x).\

ƒ ደግሞ በወሰኖች [a, b] መካከል ተጠራዥ ቢሆን፣ እንግዲህ

\int _{a}^{b}f(x)\,dx\,=\int _{a}^{b}g'(x)\,dx\,=\int _{a}^{b}d(g(x))\,=g(b)-g(a)

እዚህ ላይ ማስተዋል ያለብን ይሄ ክፍል ƒ የማያቋርጥ አስረካቢ እንዲሆን አይፈልግም

ምሳሌዎች

\int _{0}^{\pi }\cos(x)dx=\sin(\pi )-\sin(0)=0

\int _{1}^{e}{\frac {dx}{x}}=\ln(e)-\ln(1)=1

እርግጡ ምን ማለት ነው?

የካልኩለስ መሰረታዊ እርግጥ በቀላሉ ሲቀመጥ እንዲህ ይላል፡ በአንድ ብዜት ውስጥ የሚታዩ ኢምንት ለውጦች ሲደመሩ ውጤታቸው በዚያ ብዜት ውስጥ ከሚታየው አጠቃላይ ለውጥ ጋር እኩል ነው።

ለምሳሌ፡ አንድ እኑስ በቀጥታ መስመር ቢጓዝና ከጊዜ አንጻር ያለው አቀማመጥ x, በአስረካቢ x(t) ቢገኝ፣ t ጊዜ ቢሆን፣ የዚህ አስረካቢ ከጊዜ አንጻር ያለው ውድድር የአቀማመጡ ኢምንት ለውጥ dx, ለኢምንት ጊዜ dt ሲካፈል ነው ማለት ነው። ይሄ እንግዲህ በሥነ እንቅስቃሴ ፍጥነት የሚባለው ነው

{\frac {dx}{dt}}=v(t).

ስለሆነም

dx=v(t)\,dt.

እንግዲህ በካልኩለስ እርግጥ መሰረት ማንኛውም የአቀማመጥ ለውጥ x (or Δx) ኢምንት ለውጦቹን dx በመደመር ይገኛል ማለት ነው። ኢምንቶችን ለመደመር አዕላፍ ጊዜ መደመር ስለሚያስፈልግ፣ ይህ ተግባር ጥረዛ ይሰኛል ማለት ነው። በጥረዛው ወቅት፣ የአቀማመጥ ውድድር በኢምንት ጊዜ ተባዝቶ እንደሚደመር ልብ ማለት አስፈላጊ ነው።

ስለሆነም፣ ጥረዛው ከውድድሩ ተነስቶ የመጀመሪያውን አስረካቢ ያስገኛል ማለት ነው። በዚህ ተገላቢጦሽ፣ ከጥረዛ ውጤት ተነስተን በማወዳደር የመጀመሪያውን አስረካቢ ማግኘት እንቻላለን።

ማጣቀሻ

Apostol 1967, §5.1
Apostol 1967, §5.3

ተጨማሪ ንባብ

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Apostol 1967, §5.1

[2] Apostol 1967, §5.3