Warmteoordragskoëffisiënt
Warmteoordragskoëffisiënt in termodinamika en in meganiese ingenieurswese is die eweredigheidskonstante tussen hittestroom en die termodinamiese dryfkrag vir die vloei van hitte.

Formule
Wanneer die hitteoordrag of hittelas (Q) van 'n hitteruiler bepaal word, word die volgende formule gebruik:
- (Omdat U gebaseer is op die buis buitediameter, gebruik ook die buitediameter wanneer die area bereken word)
Waar:
- = hitteoordrag [Watt]
- = warmteoordragskoëffisiënt [W/(m2.K)]
- = oordragoppervlak in vierkante meter
- = Gemiddelde temperatuurverskil [°C]
- = Logaritmies gemiddelde temperatuurverskil [°C]
- = Temperatuur korreksiefaktor. Dit is 'n funksie van die hoeveelheid gange van die hitteruiler en die posisie van die in- en uitlate van die hitteruiler.
- = Aantal buise
- = Buis buitediameter [meter]
- = Buislengte [meter]
Gebruik altyd eenhede sodat die linkerkant gelyk is aan die regterkant.
Kompenseer warmteoordragskoëffisiënt vir snelheid
Omdat die warmteoordragskoëffisiënt 'n funksie is van vloeisnelheid (kyk later), kan dit soos volg gekompenseer word vir snelheid:
Waar:
- = Vloei. Vir die hoogste akkuraatheid moet volumevloei of vloeisnelheid gebruik word, veral vir gasse waar die digtheid 'n sterk funksie van temperatuur is. Omdat hierdie metode egter 'n benaderde metode is kan massavloei of molvloei ook gebruik word indien temperature nie baie verander nie.
- , = Verwysingsvloei aan die warm en koue kant (gebruik verkieslik volumevloei of vloeisnelheid)
- , = Werklike vloei aan die warm en koue kant.
- , = warm en koue eksponente wat eksperimenteel verkry word. In Aspen Plus weergawe 10 se HeatX-blok word die verstekwaardes gegee as x = 0.6 en y = 0.8
- = Berekende warmteoordragskoëffisiënt by ,
- = Verwysingswarmteoordragskoëffisiënt by ,
Hitteruiler monitering
Wanneer 'n hitteruiler se prestasie deur middel van sy warmteoordragskoëffisiënt gemoniteer word, is dit belangrik om te kompenseer vir snelheid. Dit kan soos volg gedoen word:
Bepaling van verwysingswaardes en eksponente
Die verwysingswaardes en eksponente (, , , ) kan verkry word deur werklike data te gebruik en hierdie waardes so te verander dat die berekende warmteoordragskoëffisiënt () so min as moontlik 'n funksie van vloei is. Dus moet dit nie verander wanneer vloei verander nie.
Formule vir warmteoordragskoëffisiënt vir 'n buis en mantel hitteruiler
Die warmteoordragskoëffisiënt vir 'n hitteruiler, gebaseer op die buis te buitediameter, word soos volg weergegee:
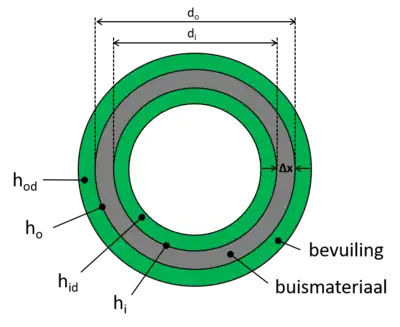
Geleidingsterm
In Warmteoordrag word die geleiding van 'n hol silinder afgelei asː
En die hitte-oordrag weerstand asː
Indien hierdie term met gemaal word, word die geleidingsterm verkryː
Dusː
Die gelykdingsterm kan ook soos volg vereenvoudig word:
Afkortings
Die volgende afkortings is van toepassingː
- = hitteoordragskoëffisiënt [W/(m2.K)]
- = buis buitediameter [m]
- = buis binnediameter [m]
- = buite filmkoëffisiënt [W/(m2.K)] (Bereken soos bo gewys)
- = binne filmkoëffisiënt [W/(m2.K)] (Bereken soos bo gewys)
- = buite bevuilingskoëffisiënt [W/(m2.K)] (Lees af uit tabelle)
- = binne bevuilingskoëffisiënt [W/(m2.K)] (Lees af uit tabelle)
- = termiese geleiding van buismateriaal [W/(m.K)]
- = wanddikte van buis [m]
- = temperatuur [°C]
- = snelheid [m/s]
- = snelheid van water [m/s]
- = dightheid[kg/m3]
- = viskositeit by gemiddelde vloeiertemperatuur [Ns/m]
- = viskositeit by buiswand [Ns/m]
- = vloeier spesifieke warmtekapasiteit [J/(kg.K)]
- = vloeier termiese geleiding [W/(m.K)]
Filmkoëffisiënte (hi en ho)
Die filmkoëffisiënte ( en ) word met die volgende formules hieronder bereken.


Buiskant
Vir die buiskant word vervang met en word vervang met "".
Die vloeisnelheid aan die buiskant word eenvoudig soos volg bepaal:
Waar:
- = vloeisnelheid in die buise (m/s)
- = massavloei (kg/h)
- = dightheid (kg/m3)
- = totale aantal buise (die aantal gate in die buisplaat)
- = aantal buisgange (Engelsː "passes") van hitteruiler
- = buis binnediameter (meter)
Mantelkant
Vir die mantelkant word vervang met en word vervang met met die hidrouliese diameter, .
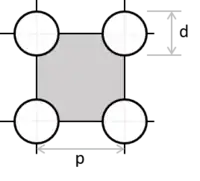
Diameter
Vir 'n vierkantige buiskonfigurasie word die volgende formule gebruik:
Vir 'n driehoekige buiskonfigurasie word die volgende formule gebruik:
Waarː
- = buisspasiëring
- = buis se buitediameter
Hierdie twee formules word afgelei in hidrouliese diameter.
Snelheid
Die snelheid is nodig om die Reynoldsgetal uit te werk. Om die snelheid te bepaal word die vloei loodreg met die buise tussen die keerplate by die ewenaar van die hitteruiler beskou.
Die deursnitarea by die ewenaar van die hitteruiler word soos volg bereken:
Dus is die snelheid aan die mantelkant die volgende:
Waar:
- = Effektiewe deursnit vloeiarea
- = Binnediameter van die hitteruiler mantel
- = Keerplaat spasiëring (afstand tussen keerplate)
- = Buis spasiëring
- = Buis buitediameter
- = Snelheid aan die mantelkant
Formules
Die volgende formules word vir beide die buiskant en mantelkant gebruik.
Vir die buiskant word , , vervang met , , .
Vir die mantelkant word , , vervang met , , .
- = 0.021 vir gasse
- = 0.023 vir nie-viskose vloeistowwe
- = 0.027 vir viskose vloeistowwe
Benadering vir water
Vir water kan die volgende benadering gebruik word:
Hierdie wys ook dat sou alle ander parameters dieselfde bly, dan geld in die algemeenː
Dittus–Boelter equation
Die Dittus–Boelter-vergelyking (vir turbulente vloei) soos ingestel deur W.H. McAdams is 'n eksplisiete funksie vir die berekening van die Nusselt-getal. Dit is maklik om op te los, maar is minder akkuraat wanneer daar 'n groot temperatuurverskil oor die vloeistof is. Dit is aangepas vir gladde buise, so gebruik vir growwe buise (meeste kommersiële toepassings) word gewaarsku. Die Dittus–Boelter-vergelyking is:
waar:
- binnediameter van 'n sirkelvormige buis
- is die Prandtl getal
- vir die warm vloeier en vir die koue vloeier.
Die Dittus–Boelter vergelyking is geldig vir:
Die Dittus–Boelter-vergelyking is 'n goeie benadering waar temperatuurverskille tussen massavloeistof en hitte-oordragoppervlak minimaal is, wat vergelykingskompleksiteit en iteratiewe oplossing vermy. Neem water met 'n grootmaat vloeistof gemiddelde temperatuur van 20°C (68 °F), viskositeit Pa.s en 'n hitte-oordrag oppervlak temperatuur van 40°C (viskositeity Pa.s . Dit gee 'n viskositeit korreksiefaktor van 10.07/6.96 = 1.45. Dit verhoog tot 3.57 met 'n hitte-oordrags oppervlak temperatuur van Sjabloon:Cvt (viskositeit Pa.s), wat 'n wesenlike verskil aan die Nusselt getal maak en daarom ook die hitte-oordragskoëffisiënt.
Termiese geleiding (kw)
| Temperatuur | Termiese geleiding [W/(m.K)] | ||
| Kelvin | °C | Aluminium | Yster |
|---|---|---|---|
| 10 | -263.15 | 38000 | 710 |
| 20 | -253.15 | 13500 | 1000 |
| 40 | -233.15 | 2300 | 560 |
| 60 | -213.15 | 850 | 270 |
| 80 | -193.15 | 380 | 170 |
| 100 | -173.15 | 300 | 132 |
| 200 | -73.15 | 237 | 94 |
| 300 | 26.85 | 273 | 80 |
| 400 | 126.85 | 240 | 69 |
| 500 | 226.85 | 237 | 61 |
| 600 | 326.85 | 232 | 55 |
Kyk:
- "Perry's Chemical Engineers' Handbook", 6de uitgawe, bladsy 3-261
- Engineering toolbox/Thermal conductivity
Tipiese warmteoordragskoëffisiënte (U)
Die volgende is 'n lys van tipiese warmteoordragskoëffisiënteː
| Produkte | U [W/(m2.K)] | Ander beskrywing |
|---|---|---|
| Vrye konveksie gas - Vrye konveksie gas | 1-2 | Tipies 'n venster: kamer na buitekant deur glas |
| Vrye konveksie gas - Geforseerde vloeistof vloeiende water | 5-15 | Tipies 'n verkoeler vir sentrale verhitting |
| Vrye konveksie gas - Gekondenseerde waterdamp | 5-20 | Tipiese stoomverkoelers |
| Geforseerde konveksie vloeiende gas - Vrye konveksie gas | 3-10 | Oorverhitters |
| Geforseerde konveksie vloeiende gas - Geforseerde konveksie gas | 10-30 | Hitteruilergasse |
| Geforseerde konveksie vloeiende gas - Geforseerde vloeistof vloeiende water | 10-50 | Gas verkoelers |
| Geforseerde konveksie vloeiende gas - Gekondenseerde waterdamp | 10-50 | Lugkoelers |
| Vloeistofvrye konveksie - Geforseerde konveksie gas | 10-50 | Gas ketel |
| Vloeistofvrye konveksie - Vrye konveksie vloeistof | 25-500 | Oliebad vir verhitting |
| Vloeistofvrye konveksie - Geforseerde vloeistof vloeiende water | 50-100 | Verhittingsklos in water, water sonder vloeimanipulasie |
| 500-2000 | Verhittingsklos in water, water met vloeimanipulasie | |
| Vloeistofvrye konveksie - Gekondenseerde waterdamp | 300-1000 | Stoommantel rondom houer met roerders, water |
| Vloeistofvrye konveksie - Gekondenseerde waterdamp | 150-500 | Ander vloeistowwe |
| Geforseerde vloeistof vloeiende water - Vrye konveksie gas | 10-40 | Ontbrandingskamer en straling |
| Geforseerde vloeistof vloeiende water - Vrye konveksie vloeistof | 500-1500 | Verkoelingsklos - geroer |
| Geforseerde vloeistof vloeiende water - Geforseerde vloeistof vloeiende water | 900-2500 | Hitteruilers: water/water |
| Geforseerde vloeistof vloeiende water - Gekondenseerde waterdamp | 1000-4000 | Kondenseerder: stoom na water |
| Kokende water (vloeistof) - Vrye konveksie gas | 10-40 | Stoomketel en straling |
| Kokende water (vloeistof) - Geforseerde vloeistof vloeiende water | 300-1000 | Verdamping van verkoelers of pekelverkoelers |
| Kokende water (vloeistof) - Gekondenseerde waterdamp | 1500-6000 | Verdampers: stoom/water |
Kyk:
- "Chemical Engineering", Coulson and Richardson, Volume 6, 2de uitgawe, bladsy 580
- Engineering toolbox/overall heat transfer coefficient
Engelse terme
- Gas ketel = Gas boiler
- Gasverkoeler = Gas cooler
- Geforseerde konveksie gas = Forced convection gas
- Geforseerde konveksie vloeiende gas = Forced convection (flowing) gas
- Geforseerde vloeistof vloeiende water = Forced liquid (flowing) water
- Gekondenseerde waterdamp = Condensing vapor water
- Hitteruiler = Heat exchanger
- Kokende water (vloeistof) = Boiling liquid water
- Kondenseerder = Condenser
- Lugverkoelers = Air cooler
- Mantel = Jacket
- Oliebad = Oil bath
- Ontbrandingskamer = Combustion chamber
- Pekel = Brine
- Roerder = Stirrer
- Stoomketel = Steam boiler
- Straling = Radiation
- Superheater = Oorverhitter
- Verdamper = Evaporator
- Verdamping = Evaporation
- Verhittingsklos = Heating coil
- Verkoeler = Radiator
- Verkoeler = Refrigerator
- Verkoelingsklos = Cooling coil
- Vloeimanipulasie = Steering
- Vloeistofvrye konveksie = Liquid free convection
- Vrye konveksie gas = Free convection gas
- Vrye konveksie vloeistof = Free convection liquid
Bronne
- Coulson & Richardson, Chemical engineering, Volume 6, Hersiene 2de uitgawe, bladsy 608