Logiese hek
'n Logiese hek voer logiese bewerkings uit op een of meer logiese toevoere en lewer 'n enkele logiese afvoer. Die logika wat gewoonlik uitgevoer word is Boolse logika en word algemeen aangetref in digitale stroombane. Logiese hekke word hoofsaaklik elektronies met behulp van diodes of transistors aanmekaargesit, maar kan ook gebou word met relês, hidroliese, optiese of selfs meganiese elemente.
Logiese toestande
'n Boolse logiese toevoer of afvoer kan altyd slegs een van twee toestande aanneem. Hierdie logiese toestande kan 'n verskeidenheid name hê insluitende: aan / af, hoog (H) / laag (L), een (1) / nul (0), waar (W) / Vals (V), positief (+) / negatief (-), positief / grond, oop stroom/ geslote stroom, potensiaalverskil / geen verskil.
Om konsekwent te wees word die name 1 en 0 hieronder gebruik.
Logiese hek
'n Logiese hek neem een of meer logiese-toestand toevoere en lewer 'n enkele logiese-toestand afvoer. Omdat die afvoer ook 'n logiese toestand is, kan die afvoer van een logiese hek verbind word aan die toevoer van ander (een of meer) logiese hekke. Twee afvoere kan egter nie aanmekaar verbind word nie, aangesien hulle moontlik kan probeer om verskillende logiese toestande te lewer. In elektroniese logiese hekke, sal dit lei tot 'n kortsluiting. Met elektroniese logika, word 'n logiese toestand verteenwoordig deur 'n sekere spanning (wat sal afhang van die soort logika wat gebruik word). Elke logiese hek vereis elektriese krag om die elektriese strome te manipuleer om die korrekte afvoerspannings te lewer. In logiese stroombaandiagramme word die elektriese krag nie aangetoon nie, maar in volledige elektroniese tekeninge moet die kragverbindings aangetoon word.
Basiese logiese hekke en hul meganiese eweknieë
Alhoewel halfgeleier elektroniese logika vir die meeste toepassings verkies word, word relês en ander soorte skakelaars steeds in sommige nywerheidstoepassings asook vir opvoedkundige doeleindes aangewend.
Relê-logika was geskiedkundig belangrik vir outomatisering in nywerhede. In relê-logika is die twee logiese toestande 'oop stroombaan' en 'geslote stroombaan'. Die elektriese sein is ekstra en kan enige spanning of stroom hê en in enige rigting vloei.
In elektroniese stroombane, word die spannings van die logiese toestande vasgestel. Dit is nie moontlik om enige ander sein deur die hekke te stuur nie, aangesien die logiese toestande die enigste moontlike spannings is. Vir meer inligting oor hoe moderne halfgeleier logiese hekke werk, sien CMOS.
Die drie belangrikste logiese hekke is die EN-, die OF- en die NIE-hekke. Met dié drie kan enige denkbare Boolse vergelyking gebou word. Vir gerief word die afgeleide soorte, naamlik die NEN, NOF, XOF en XNOF ook gebruik, wat dikwels minder stroombaanelemente vir 'n gegewe vergelyking vereis as 'n implementering wat uitsluitlik op die EN-, OF- en NIE-hekke gebaseer is. Die NEN-hek het inderwaarheid die laagste komponenttelling van enige hek buiten die NIE-hek wanneer dit met moderne halfgeleiertegnieke aanmekaargesit word en aangesien 'n NEN beide 'n NIE en, deur die toepassing van De Morgan se wet, 'n OF-funksie kan implementeer kan hierdie enkele hek effektief die EN-, OF- en NIE-hekke vervang wat dit die enigste hek maak wat werklik in 'n stelsel benodig word. Programmeerbare logiese matrikse sal dikwels niks anders as NEN-hekke bevat nie om sodoende hulle interne ontwerp te vereenvoudig.
EN-hekke

Die eerste voorbeeld is die EN-hek, waarvoor die waarheidstabel hieronder links aangedui word. Die afvoer is 1 as beide toevoer A en toevoer B 1 is. In alle ander gevalle is die afvoer 0.
In geskakelde stroombaan, is die stroombaan geslote wanneer beide A en B skakelaars aan is, anders is die stroombaan oop.
| Toevoer | Afvoer | |
|---|---|---|
| A | B | A EN B |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
OF-hekke

'n Ander belangrike samestelling is die OF-hek, waarvan die waarheidstabel hieronder links vertoon word. Die afvoer is 1 wanneer die toevoer A of toevoer B 1 is. Die afvoer is ook 1 as beide toevoere 1 is.
In die skakelaarstroombaan, is die stroombaan geslote wanneer skakelaar A of skakelaar B (of beide) aangeskakel word, andersins is die stroombaan oop.
| Toevoer | Afvoer | |
|---|---|---|
| A | B | A OF B |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
NIE-hekke

'n Eenvoudiger samestelling is die NIE-hek, waarvan die waarheidstabel hier langsaan vertoon word. In die NIE-hek is die afvoer die logiese teenoorgestelde van die toevoer. Dit beteken dat as die toevoer 1 is, dat die afvoer 0 gaan wees en as die toevoer 0 is dat die afvoer 1 gaan wees.
In die skakelaarstroombaan word 'n skakelaar gebruik wat normaalweg aangeskakel is om 'n geslote stroombaan te lewer. As die skakelaar gedruk word verander die stroom in 'n oop stroombaan.
| Toevoer | Afvoer |
|---|---|
| A | NIE A |
| 0 | 1 |
| 1 | 0 |
NEN-hekke

Die NEN-hek is die NIE van 'n EN-hek. Dit wil sê die afvoer is 1 wanneer A en B nie 1 is nie, soos gesien kan word in dié waarheidstabel.
| Toevoer | Afvoer | |
|---|---|---|
| A | B | A NEN B |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
NOF-hekke
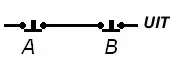
Die NOF-hek is die NIE van 'n OF-hek. Dit wil sê dat die afvoer 1 is slegs wanneer beide toevoere 0 is, soos aangedui in dié waarheidstabel.
| Toevoer | Afvoer | |
|---|---|---|
| A | B | A NOF B |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
XOF- en XNOF-hekke
Daar bestaan nog twee 'basiese' hekke – XOF (eksklusiewe OF) en XNOF (eksklusiewe NOF).
XOF is 'n 'strenger' weergawe van die OF-hek. In plaas van dat die afvoer 1 is wanneer enige van die toevoere 1 is, het die XOF-hek 'n 1 as afvoer wanneer slegs een van die toevoere 1 is, soos gesien kan word in die onderstaande waarheidstabel. In die geval van 'n meervoudige toevoer XOF-hek sal die afvoer 1 wees wanneer daar 'n onewe getal 1'e as toevoer is.
| Toevoer | Afvoer | |
|---|---|---|
| A | B | A XOF B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
XNOF is 'n omgekeerde weergawe van die XOF-hek, soos gesien kan word in die onderstaande waarheidstabel. Dit kan ook gesien word as 'n 1 afvoer wanneer die toevoere gelyk is.
| Toevoer | Afvoer | |
|---|---|---|
| A | B | A XNOF B |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Die voorafgaande eenvoudige logiese hekke kan gekombineer word om meer komplekse Boolse logikastroombane te vorm. Logiese stroombane word gereeld geklassifiseer in twee groepe: kombinasie logika, waar die intrees kontinue-tyd funksies van die toevoere is, en sekwensiële logika, waar die afvoere afhanklik is van die inligting gestoor deur die stroombane sowel as die toevoere.